2017's Most Popular...
By The Editors
The most popular articles, blogs, podcasts, and videos on our website over the year, 2017.
January 3, 2018
From The Staff Communications
In compiling a top-10 list of the year’s most popular content on American Scientist, we had data from essentially two different websites: one before and one after June 22, 2017, which is when we went live with our new, mobile-friendly website with publications back to 2012.
Our in-house, online archive goes back to 1998, which users had access to via the old site, and so some of those pre-2012 articles made our top-10 list for the first half of 2017! (By the way, you can access our 1913–2012 archive as scanned pages.)
We're getting close to completing our conversion of those 14 years of content (1998–2011) so that it will be available online, and will update this page with new links to those older articles once that is done. So here's our most popular online content—first the top-10 from our old site and then the top-10 from our new one. At the end, find our top-3 videos and podcasts.
Happy 2018!
#10 (old site)
Religious pamphlets by leading scientists of the Scopes era provide insight into public debates about science and religion.
(May–June 2005 by Edward Davis)

#9
There’s a fundamental inequity in recommending that job seekers apply for every possible scholarly position to improve their odds of an offer.
(June 2, 2017 by Christie Bahlai)

#8
We don’t know how long or which grants are frozen at the U.S. Environmental Protection Agency right now, but when my funds were frozen in 2007 it was devastating.
(January 27, 2017 by Lisa Hayward)

#7
Recent data help explain how this famous group of Galapagos birds evolved, although gaps in our understanding remain.
(March–April, 2002 by Peter Grant)

#6
These ambling, eight-legged microscopic “bears of the moss” are cute, ubiquitous, all but indestructible, and a model organism for teaching science.
(September–October 2011 by William R. Miller)

#5
Few remember the man who discovered the “molecule of life” three-quarters of a century before Watson and Crick revealed its structure.
(July–August 2008 by Ralf Dahm)
#4
At one time or another, most of us have proved empirically, and painfully, the old mother’s tale that it’s possible to get sunburned on a cloudy day.
(May–June 2006 by David Schoonmaker)

#3
Your parents went halfsies on much of your biological material (for example, your chromosomes), but one of the most important pieces of your cellular machinery came almost exclusively from your mom: mitochondria.
(May 10, 2015 by Katie L. Burke)
#2
Having babies isn’t easy—and the standard explanation may be wrong.
(November–December 2013 by Pat Shipman)
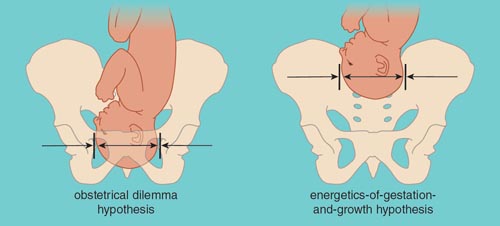
#1 (old site)
If the reader is to grasp what the writer means, the writer must understand what the reader needs.
(November–December 1990 by George Gopen and Judith Swan)
Update (January, 2018): This article was republished in 2008 in a "classics" section of our old website no longer available. The full feature is now available in The Long View blog.

Data-dependent analysis—a “garden of forking paths”— explains why many statistically significant comparisons don't hold up.
(November–December, 2014 by Andrew Gelman and Andrew Gelman )

#9
A "classic" book review from 1969 of the book by the same name.
(November–December 2012 by Mary S. Calderone)

#8
Scans of implant patients deaf in only one ear, before and after the procedure, have uncovered how quickly the cortex can rewire itself.
(July 12, 2016 by Michael Dorman)
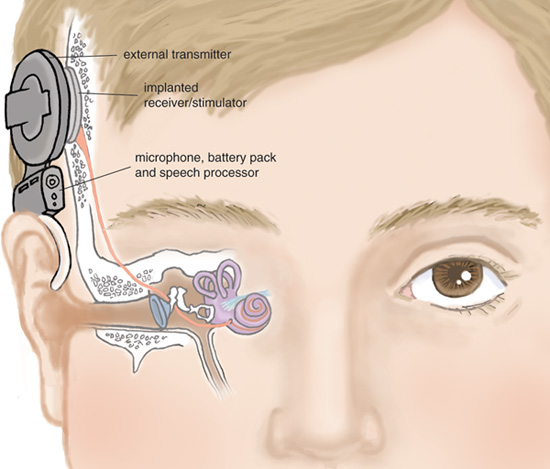
#7
Defining what truth means and deciphering how human brains verify information are some of the challenges to battling widespread falsehoods.
(November–December 2017 by Brian G. Southwell, Emily A. Thorson, and Laura Sheble)

#6
To encourage replication, work to build the standards, techniques, incentives, and institutions needed to support the grand edifice of future science.
(October 17, 2017 by Shlomo Engelson Argamon)

#5
Evidence of meat-eating among our distant human ancestors is hard to find and even harder to interpret, but researchers are beginning to piece together a coherent picture.
(March–April 2016 by Briana Pobiner)

#4
Having babies isn’t easy—and the standard explanation may be wrong.
(November–December 2013 by Pat Shipman)

#3
The two fields' intertwined histories show that most theoretical breakthroughs are preceded by the kind of deep observational work that has fallen out of vogue in the past half century.
(September–October 2017 by John G. T.
Anderson)

#2
Comparing protein levels in blood samples from those with and without an extra 21st chromosome suggests that the underlying pathology is immune dysfunction.
(Published mid-December, 2017 in advance of the issue, this one has had a lot of following online: January–February 2018 by Katie L. Burke)
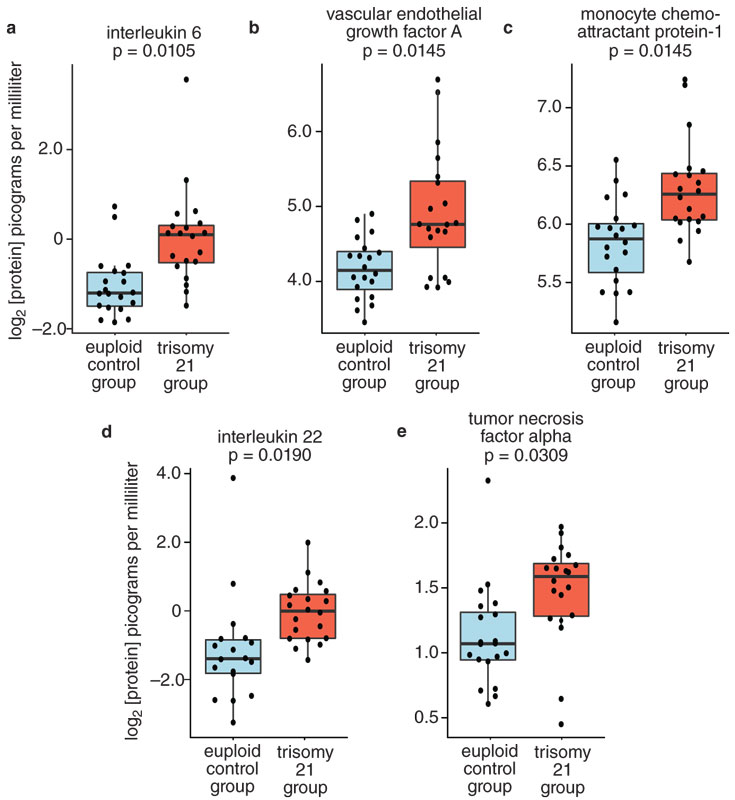
#1
A century after Ernst Mach and Albert Einstein cast doubt on absolute space, we still don't know how a gyroscope stays pointed in a fixed direction.
(November–December 2017 by Tony Rothman)

#3 A Slow Split by Robert Frederick
#2 The Biology of Cannabis by Katie L. Burke
#1 Understanding The CRISPR Craze by Robert Frederick
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.