Science Comics' Super Powers
By Matteo Farinella
Communicators are turning to comics to make science pop.
Communicators are turning to comics to make science pop.

The first time that comics and science met, it did not go well. Psychiatrist Fredric Wertham was studying delinquent youth in New York City in the late 1940s and 1950s, when he noticed that many of his patients were reading cheap booklets called comics. He was shocked to find out that these comics were filled with horror and violence. In his popular book Seduction of the Innocent (1954), Wertham claimed that comics were corrupting their young, susceptible readers. These comments gave scientific credibility to an already widespread prejudice against comics voiced by contemporary authors such as Sterling North, who wrote in a Chicago Daily News editorial: “Badly drawn, badly written and badly printed—a strain on young eyes and young nervous systems—the effect of these pulp-paper nightmares is that of a violent stimulant.”
In the following years, a wave of concerned parents and educators banded together to “break the comic magazine,” leading to hearings by the U.S. Senate Subcommittee on Juvenile Delinquency and the establishment of the Comics Code Authority, which stunted comics’ growth for decades to come. These events, which are often told as a preamble to the birth of the underground “comix” of the 1960s and 1970s, were also a huge blow for anyone who hoped to use comics in the classroom.

Image courtesy of miSci, the Museum of Innovation and Science.
Wertham’s mistake was focusing too much on the content of comics (admittedly not the most edifying stories) instead of on the widespread appeal of the medium. If he had paid more attention, he would have noticed that in the 1940s and 1950s not only the “delinquent youth” were reading comics, but so were pretty much any teenagers who could scrape together the few cents to buy them. Instead of fearing and repressing comics, scientists should have tried to understand what makes them so compelling to young readers and use that information to their advantage. Had they done so, maybe today more people would know science through comic adventures instead of tedious lab demonstrations.
To their credit, some educators of the time, such as W. W. D. Sones in The Journal of Educational Sociology, recognized the potential of comics and advocated for their introduction in the classroom (similar ideas have recently been revived by educators such as Gene Yang and Nick Sousanis). Unfortunately, these remained isolated voices, and comics have become largely synonymous with superheroes and childish entertainment, at best tolerated but often frowned upon by respectable adults—at least in the United States (Japan has a long and rich tradition of educational manga). If scientists appeared in them, it was as evil supervillains or mad assistants. There were a few notable exceptions, such as the Adventures in Science series published by General Electric, or the Cartoon Guide series by Larry Gonick, who in the 1980s and 1990s covered everything from history to calculus. The field of educational comics didn’t begin to blossom, however, until two decades ago.
After graphic novels such as Art Spiegelman’s Maus, Joe Sacco’s Palestine, and Marjane Satrapi’s Persepolis proved to the world that nonfiction comics could successfully tackle complex issues such as history and politics, the first biographies of scientists started to appear, such as Apostolos Doxiadis’s and Christos Papadimitriou’s Logicomix, Lauren Redniss’s Radioactive, and Jim Ottaviani and Leland Myrick’s Feynman. At the same time, comic strips written by scientists such as Randall Monroe’s xkcd, Jorge Cham’s PhD comics, and Rosemary Mosco’s Bird and Moon were taking over the internet. With their witty humor, these authors were able to attract readers who were not traditionally interested in science and, at the same time, familiarize scientists with comics.
Comic books with a more explicit educational purpose soon followed, both for adults (The Stuff of Life, Psychiatric Tales, and Neurocomic, which I coauthored) and for children (First Second launched an ongoing series of Science Comics in 2016). Webcomics inspired by science also continue to be very popular: The European Research Council is sponsoring a series of online comics, and major scientific journals such as Science and Nature also started to experiment with the medium (General Relativity by Adrian Cho, Science, March 2015; The Fragile Framework by Richard Monastersky and Nick Sousanis, Nature, November 2015). More recently, even academic publishers finally embraced comics as serious scholarship (Nick Sousanis’s Unflattening and Clifford Johnson’s The Dialogues: Conversations about the Nature of the Universe).
Today there are countless examples of science comics. Drawn by scientists turned cartoonists, illustrators passionate about science, or exclusive collaborations between the two (see Mysteries of the Quantum Universe by Thibault Damour and Mathieu Burniat, or Out of Nothing by Daniel Locke and David Blandy), the creation of science comics is driven by different motivations (see the 2018 article by Jordan Collver and Emma Weitkamp) and produces equally diverse results. Instead of attempting a comprehensive review or classification of “graphic science” (see an updated list on cartoonscience.org), it may be more useful to explore why comics are becoming such a popular medium for science communication.
Illustrations have always played a central role in science education and communication. Indeed, several studies have shown that diagrams, maps, and other traditional forms of scientific visualization are not merely decorative but can significantly improve learning. A well-crafted illustration follows basic design and cognitive principles, aimed to highlight structure, function, and relationships between the parts of a system, which is something that comics can also do extremely well. Although at first glance we may be attracted by the flashy artwork, and we may tend to associate comics with picture books or animations, comics have much more in common with graphic design and technical drawing. Comics are not just pictures, and not even words plus pictures. Comics are first and foremost a “sequential art” (as defined by Will Eisner and Scott McCloud), and the shape, size, and relationship between panels can convey as much information as the text itself. For this reason, many comic scholars have focused on the transitions between panels and argued that the layout or “braiding” of a comic is just as important (if not more so) as the quality of the writing and the drawings.
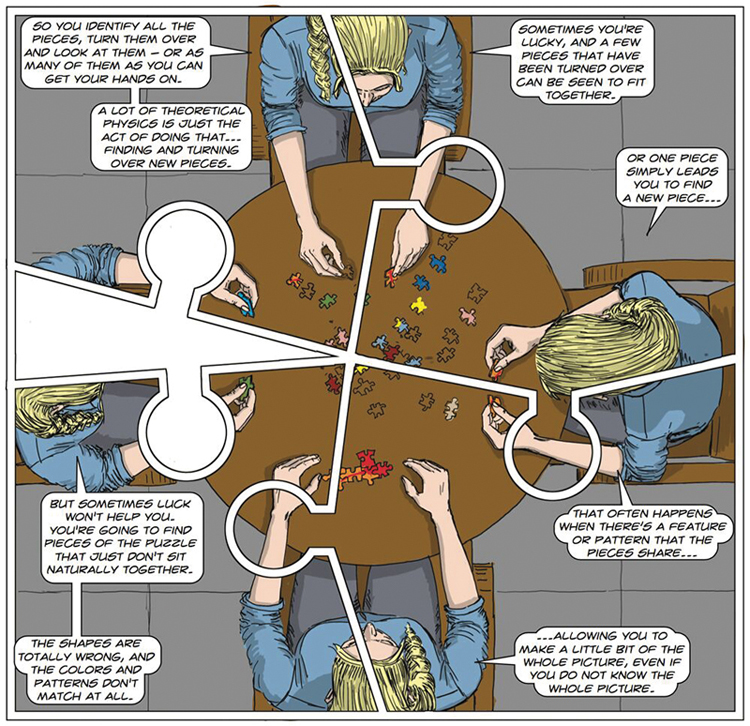
Courtesy of Clifford Johnson.
In short, the real power of comics is not to illustrate but to give structure to our thoughts, breaking down information into small digestible units (panels) and then reassembling them into the large picture. At one extreme, this presentation can be a linear sequence, just like a movie (for example, a regular grid of identical panels); but more often cartoonists have experimented with this layout, creating sequences that would be impossible to translate into words. These creative layouts could be particularly useful when it comes to science or data visualizations, because science rarely fits into a linear narrative. It often requires us to hold multiple concepts in mind, follow changes in time, and understand relationships across different scales. Some of these ideas, which may be difficult to convey with words, could be elegantly summarized by a comic page.
Behind the deceptively simple look, a carefully designed comic can combine the best of both worlds: the synthesis of a diagram with the flow of good writing. Indeed, as revealed by the cognitive scientist Neil Cohn, despite their visual format, comics are structured and perceived very much like a language; and just like written language, their function is not only to describe but also to tell engaging stories.
Narratives are a universal form of communication, and much has been written about them. One of the few things that most scholars across disciplines seem to agree about is that narratives require characters. Stories are about humans, or humanlike agents, probably because as social animals we are hardwired to care about them. Some authors went as far as suggesting that storytelling may have evolved as a sort of social or moral simulation, to better predict other people’s actions and reactions. We will never know for sure how storytelling emerged, but what is clear is that it has a strong grip on our attention. We easily get distracted halfway through a newspaper article, but we have no problem reading long novels or watching hours-long movies, because the narrative structure is intrinsically easier to follow and to remember.

From The Cartoon Guide to Genetics, courtesy of Larry Gonick.
Good science journalists understand this perfectly well, which is why they are always looking for the human angle of a story. Science communicators focus on the motivations that lead a scientist to make a certain discovery, or how that discovery could potentially change our lives. The problem is that most scientific research is a collective effort, which rarely follows a linear path and may not lead to any practical applications. Journalists tend to focus their coverage on developments in the more accessible fields of medicine, psychology, and biology at the expense of other disciplines that deal with events outside of our human scale of understanding. Simply put: It is much easier for readers to follow the story of the brave doctor who is trying to cure a terrible disease, or to watch a documentary about large mammals, than to wrap their heads around subatomic particles or the effect of ocean acidification on corals. Comics may offer a way to circumvent this problem by introducing fictional characters where no human narrators are available. Indeed, many science comics seem to adopt this strategy: In Mark Schultz’s The Stuff of Life, we witness the evolution of life on Earth through the eye of an alien scientist; in Jay Hosler’s Last of the Sandwalkers, we learn about entomology by following the adventures of some beetles; in Maris Wicks’s Coral Reef, a fish provides a tour of the reef; and in both Neuro-comic and The Quantum Universe, a fictional character is literally transported into a scientific wonderland.
These characters can help readers engage with subjects that otherwise would be too cold and distant from our everyday experience, but it is also important to consider the potential downsides of personification. Giving a smiley face to a cell or a protein necessarily distorts the science and attributes a false sense of agency to biological entities. Moreover, if characters are not matched to the message and subject matter, they may lead to confusing results. For example, in Science Comics: Plagues (2017), bacteria and viruses are depicted as much more likeable characters than our own immune cells, leading to surreal scenes such as the one in which a cute bubonic plague character cheerfully describes the horrible symptoms it causes.
Last, but not least, an important contribution that comics could bring to science communication is their use of metaphors. Of course, metaphors are not unique to comics. Language is full of them, and science journalism makes no exception. What sets comics apart from other forms of storytelling is that their own language is built upon visual metaphors. Starting from the balloons that we mentally read as speech, to motion lines, impact flashes and upfixes above a character’s head (such as droplets of sweat to signify stress or stars for pain), comics have developed a whole vocabulary of symbols to visualize invisible entities with static lines.
What sets comics apart from other forms of storytelling is that their own language is built upon visual metaphors.
Maybe this is why science comics seem to be particularly suited to extended visual metaphors. Immune cells can become policemen in a constant war against germs, the brain can become a forest of neurons, and online activity can project a digital shadow, just to name a few examples. These metaphors, far from being mere narrative devices, have the potential to make abstract scientific concepts more tangible and accessible to a nonexpert audience. Moreover, beyond simple understanding, it has been shown that metaphoric framing can affect attitudes (and possibly behavior) toward scientific and health information. In a 2015 study, Norbert Schwartz and his colleagues found that thinking of the “war against cancer” may motivate some patients but also dissuade preventive behaviors among healthy individuals (because we do not usually associate self-limitation with strength and aggressiveness). Similarly, in a recent New Yorker article Siddhartha Mukherjee suggested that it may be more productive to think of cancer as an invasive species and study which body ecosystems make it thrive instead of trying to fight the cancer cells themselves.
Indeed, some historians have argued that metaphors played a central role in scientific progress. Especially when we first encountered new invisible entities, describing them in terms of more familiar objects may have helped us come up with useful models and predictions. For example, comparing electricity to liquid or water evokes the flow of electricity. Comics can easily build upon the metaphors that are already part of the scientific jargon, making them more vivid and memorable to readers.
There are many aspects of comics that make them a promising tool for science communication. Comics can combine engaging storytelling with the structure of diagrams, they allow us to travel into distant worlds with fictional characters, and they map abstract concepts onto more familiar ones with metaphors. A more fundamental question, however, remains to be answered: Do comics actually improve learning or engagement with science?
This question is difficult to answer, and empirical studies on the educational effects of comics are scarcer than science comics themselves. A 2011 study by Jay Hosler and K. B. Boomer reported that a comic book of their own design (Optical Allusions) was just as effective as a traditional textbook when teaching concepts of evolutionary biology to college students. Moreover, the comic book was better than the textbook at engaging nonmajors with the subject. Similar effects were reported in a study by Amy N. Spiegel and her colleagues, who in 2013 tested comics as a way to engage high-school students with virology. Teenagers who were given science comics were almost five times more likely to continue reading materials about viruses than teenagers who read an equivalent text essay. Once again, these effects were more pronounced among students with a low science identity (meaning those who do not consider themselves a “science kind of person”).

From Neurocomic, courtesy of the author.
These first results are encouraging and suggest that the true value of comics may be engaging those readers who are less likely to seek other forms of science communication. Indeed, some studies with the general public (in Portugal and Taiwan) reported that when asked to read about science, people preferred comics to other formats. However, these studies were poorly designed and do not provide any conclusive evidence. More detailed experiments are required to understand the potential of comics and, in particular, to tease apart the effects of different comic strategies. As any comic reader will tell you, “with great powers come great responsibilities,” and comics should not be seen as a cheap trick to make science more engaging. Anthropomorphic characters and metaphors clarify as much as they distort and need to be carefully designed and evaluated. Narration and explanation should be thoughtfully integrated in a way that makes the science relevant to the story, avoiding overly didactic “comic textbooks,” which use pictures only as window dressing for the science.
Although they may be easy to read, making good comics requires as much time and skill as making a good documentary. Hence, we also need to train a new generation of science cartoonists who—just like science writers—are able to understand scientific content and translate it into their own unique visual language. At the end of the day, the communication of science in comics will be only as good as the comics themselves.
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.