American Scientist

Water runs downhill—we all know that. As a rule, it follows the path of steepest descent, seeking out the shortest and fastest route from top to bottom. So how can we make sense of meandering rivers, which wiggle-waggle down the valley, prolonging their journey to the sea and greatly lengthening their course? Why doesn't the flowing water—acting under the tug of gravity—just carve out a shortcut across all those loops?

I first encountered the mysteries of meanders in an article by Luna B. Leopold and Walter Langbein, published 40 years ago in Scientific American. They gave a lucid account of how meanders form and why they assume their characteristic sinuous shapes. I was a student at the time, and the article made a lasting impression. Not that I was inspired to go off and pursue a career in potamology, but the Leopold-Langbein theory of meanders was an eye-opener all the same. It brought home to me the curious fact that the world is a comprehensible place: You can look at a landform, say, and expect to understand what you see. The patterns of nature make sense, if you know how to read them.

Luna Leopold died last February at age 90. Reading accounts of his life and work led me back to that fondly remembered Scientific American article from 1966, as well as another article published a few years earlier in American Scientist. I found them still lucid and engaging—and yet, on reflection, not quite fully satisfying. It's not so much that the answers now seemed less compelling, but they led to many further questions, which I had lacked the wit to ask the first time around. Maybe nature is indeed comprehensible, but I couldn't say that I truly understood river meanders. So I delved deeper into the work of Leopold and his colleagues, and I looked at how others have approached the same problems. I even tried a few simplistic computer experiments of my own. After all that, there's still no shortage of questions.

Old Man River

Luna Bergere Leopold had a river meandering through his childhood. It was the Wisconsin River, which passed by an abandoned farm north of Madison where his family spent their weekends in a converted chicken coop. Luna's father was Aldo Leopold—forester, outdoorsman and pioneering conservationist, a philosopher among the lumberjacks. It was Luna Leopold who assembled and edited his father's book of essays, A Sand County Almanac, published posthumously in 1949.

Luna Leopold studied civil engineering, then meteorology and finally geology. He worked more than 20 years with the U.S. Geological Survey, including a decade as Chief Hydrologist. Then he had a second long career at the University of California, Berkeley. I think it safe to say that Leopold was the foremost American student of rivers and the landscapes they create. And he did not study them from a Washington office or a Berkeley classroom; he got his feet wet. An obituary in the Washington Postdescribed his way of life:

Well known for his scientific fieldwork, he also made bows and arrows, hunted and fished, rode horses, composed piano and guitar music, danced, flew planes, painted landscapes, wrote poetry, bound books, acted on stage, built furniture, claimed to cook strawberry shortcake in a camp Dutch oven and told campfire stories. He floated on a raft through the Grand Canyon to measure the depth of the Colorado River.

Most of Leopold's work was done in collaboration with colleagues, but for brevity in what follows I shall refer to joint work by his name alone.

Around the Bend

Leopold brought a distinctively quantitative and mathematical style to the study of rivers. For example, he formulated scaling laws that describe how the cross section of a natural channel changes as a function of the volume of water flowing through it. He even did some computer simulations—without a computer! Using shuffled decks of cards or tables of random numbers, he carried out probabilistic studies of landform features such as the branching of a drainage network.

The serpentine shapes of meanders certainly invite mathematical analysis. Although in nature the curves are highly irregular—no two alike, perhaps—Leopold argued that they all derive from a specific underlying form, which he called a sine-generated curve.

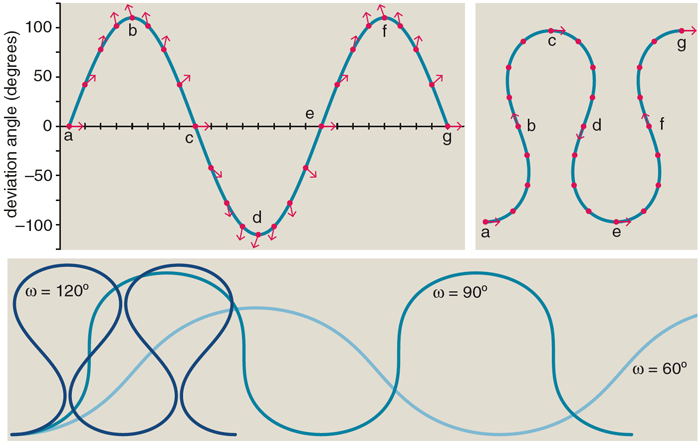
Imagine you are canoeing down a meandering river with a compass in hand, making note of your heading at regular intervals. According to Leopold, your direction should vary sinusoidally as a function of the distance you have traveled along the river centerline. This is not to say that the shape of the river itself is a sine curve; rather, the sine function specifies the heading. The governing equation is:

θ=ωsins.

Here q is the heading angle, measured with respect to the mean down-valley direction (the path the river would follow if it did not meander at all); s is distance along the stream centerline; and w is the maximum angle that the path makes with the down-valley axis. For small values of w, less than 90 degrees, the sine-generated curve has gentle undulations, so that the river weaves back and forth but at all times maintains a down-valley component of motion. At w=90 degrees, the path of the stream crosses perpendicular to the valley axis. At still larger values of w, the lobes of the curve become horseshoe-shaped, and for part of each meander cycle the river's course takes it back up the valley. A little beyond w=120 degrees, adjacent lobes of the curve begin to overlap. On graph paper the lines merely cross, but in a river this event signals the development of a "cutoff," diverting the flow and leaving behind a stranded oxbow lake.

The sine-generated curve looks like a plausible candidate for describing meanders, at least within a limited parameter range. But what made Leopold so sure it was the one right candidate? His argument goes as follows. Take two points a and b connected by a stretch of river of length L, where L is greater than the straight-line distance from a to b. Now think of all the ways of bending and folding this segment of river into a smooth curve without changing its length or detaching it from its end points. Among all such paths, the sine-generated curve has three interesting properties: It is the path of minimal bending stress, it is the path of minimal variance in direction, and it is the path representing the most likely random walk. I shall first discuss the two minimization principles and return later to the random walks.

The bending stress of a river is the work or energy that has to be expended to make its path deviate from a straight line. At each point along the route, the bending stress is proportional to the square of the curvature at that point. For a straight segment, bending stress and curvature are both zero; they increase as a turn gets sharper. Among all smooth, length-L curves from a to b, the sine-generated curve has the smallest squared curvature summed over the entire path.

Directional variance is a similar concept. As you follow the river from ato b, measure at each point along the way how much your heading deviates from the mean down-valley direction, then compute the sum of the squares of these angles. Again, the sine-generated curve yields the smallest possible total.

These properties of the sine-generated curve are mildly surprising. I would have guessed that an arc of a circle—the most symmetrical curve—would have the lowest squared curvature and directional variance, but that is not the case. (Of course a straight line is superior, but that solution is forbidden by the length constraint.)

Leopold offers a simple demonstration of how the sine-generated curve emerges as a natural solution to a problem of minimizing work or energy. If you hold the ends of a strip of spring steel so that it forms a horseshoe-shaped loop, the metal spontaneously adopts the form of a sine-generated curve. I couldn't resist trying this myself. I found that it works reliably only for single loops. If you try to fold the spring into multiple meanders, the configuration is unstable.

The Best of All Possible Meanders

Perhaps the strongest rationale in support of Leopold's theory of meanders is simply that meanders look more like sine-generated curves than like other common objects from the mathematical cupboard. But why should we expect meanders to have any simple mathematical form?

The explanations based on bending stress and directional variance rest on principles of global optimization. The favored path is one that optimizes some property measured over the entire course of the river. By choosing the path with the smallest total squared curvature, for example, the river minimizes the energy it invests in turning through sharp bends.

The physical sciences are full of such optimization laws. Optics, for example, has the principle of least time, which explains the geometry of refraction by saying that light always follows the path that can be traversed fastest. This manner of reasoning has proved very successful, and yet it can be tricky to apply. Why does light take the path of shortest travel time? And how does a photon know what angle of refraction will get it through a window-pane most quickly?

In the case of the meandering river, it's not obvious which variables ought to be optimized. Minimizing energy cost seems plausible enough, but what about directional variance? Leopold himself points out that it might make more sense to minimize the variance in curvature, so that the work of turning the river would be spread out as uniformly as possible. But that choice would favor the circle over the sine-generated curve.

It's also hard to know where to stop optimizing. The curves under discussion here are the best possible curves only if one accepts a number of constraints or assumptions, some of which seem rather arbitrary. For example, as the experiment with a steel spring reveals, bending stress can be further reduced by converting a series of little meanders into a single big one. Thus if minimal bending stress were the only criterion governing the river's plan form, all meanders would be as large as possible—but they aren't. Most meanders have a characteristic scale, proportional to the width of the river. An even more critical assumption is the fixed length L. We could make the meander problem go away altogether just by shortening the river.

Finally, to have much explanatory power, a global optimization principle needs to be linked to some local mechanism that puts it into effect. We may well calculate that a certain shape of bend minimizes energy loss, but what are the forces at each point along the river channel that create and maintain that shape? The river can't think globally; it can only act locally.

River of Randomness

The random-walk model of river meandering is one example of how a local rule—in this case aimless wandering—might give rise to large-scale regularity. The premise is that over decades or centuries, a river channel can drift over its floodplain, twisting and shifting at random (although always subject to certain constraints, such as not flowing uphill). Any configuration is possible, but all of the most likely ones, according to Leopold, look something like a sine-generated curve.

The mention of random walks in this context both intrigued and confused me. Random walks have become a common notion in recent years, and yet the kind of walk that yields the sine-generated curve was not one I had encountered before. From Leopold's description I was not able to grasp all the details. He referred to earlier work by Hermann von Schelling, but the crucial document was a 1964 technical report from the General Electric Company, which I had a hard time tracking down. Eventually I found a copy at the Smith College library.

The process studied by von Schelling is one in which a walker takes a step of unit length, turns through a randomly selected angle, takes another step in the new direction, and so on. Not just any such walk qualifies, however. To be admitted, a walk must begin by leaving point a at a specified angle; it must end by reaching point b; and in between it must cover a specified distance L. Among random paths that satisfy these constraints, von Schelling asked what the most frequent or likely paths might look like. If the walker chooses each step's direction from a uniform probability distribution (so that any angle is equally likely), von Schelling got no nontrivial answer. But he did find a solution for a walk where the turning angle at each step is drawn at random from a normal, or Gaussian, distribution with a mean of zero.

Von Schelling's mathematical solution takes the form of an integral that he found difficult to evaluate. The sine-generated curve is an approximation to the value of this integral—inexact, but quite close within the range of parameter values of interest for river meanders. Strictly speaking, the properties of minimal squared curvature and minimal directional variance have been proved only for the exact curve defined by the integral, not for the approximation. At the level of detail needed for describing river channels, however, the discrepancy is of no consequence.

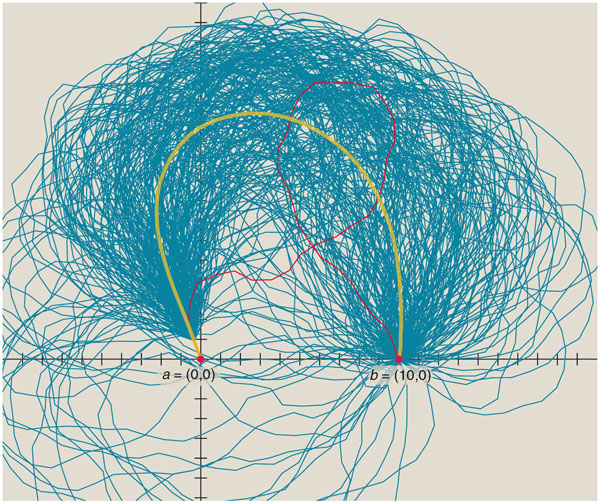
From a computational point of view, the trouble with these most-frequent random walks is that they're not nearly frequent enough. The naive algorithm for generating examples of such paths calls for launching many walkers from point a, all in the appropriate initial direction, and then discarding all walks except those that happen to reach point bafter exactly Lunit-length steps. There are infinitely many walks that satisfy these criteria, and yet the probability of ever seeing one is zero. Life is too short to wait for such events.

In order to get some rough idea of what individual von Schelling walks might look like, I have tried a sloppier algorithm. Instead of insisting that a walk end precisely at point b, I accept any walk that takes the requisite number of steps and lands within one further step of b. Even with this relaxed criterion, the algorithm is practical only for fairly short walks.

Superimposing a few hundred of these walks produces quite a frizzy hairball, but taking the average of all the paths yields a smooth arc that resembles a sine-generated curve. One peculiarity of the average walk is its asymmetry: It leans one way or the other, depending on the departure angle at point a. The reason is that we have specified the direction of the initial segment but put no constraint on the final step at b. This may have been an oversight in the way the problem was formulated by von Schelling. (On the other hand, for what it's worth, many river meanders exhibit systematic asymmetry, typically crossing the valley at a sharper angle on the upstream leg.)

A deeper perplexity awaits when we go in search of von Schelling's "most likely" or "most frequent" random walk. Should we look for it among the individual walk trajectories, or in the average of all such walks? Which of these is the right model for a river meander? Often, the terms "typical" and "average" are nearly synonymous, and Leopold clearly thought that the average would be representative of the population; "the most probable path is the average path of a random walk," he wrote. In other words, if you choose a random walk at random, it will probably be much like the average of all random walks. Von Schelling offered an analogy with thermodynamics, where uncommon events (such as perfume returning to its bottle) are so utterly improbable that we invent laws of physics to forbid them. It's a fundamental assumption, he wrote, "that in our environment random walks are approaching most frequent paths in an overwhelming majority of cases." But then he added: "This is far from being self-evident."

It's certainly not evident in the little sample of walks I generated. Not one of the individual walks looks anything like the average of all the walks. If we imagine a river channel wandering over a floodplain according to this algorithm, wouldn't a snapshot made at some arbitrary moment be likely to resemble a single random walk, rather than the average? But it's the average of the walks that corresponds more closely to the sine-generated curve and to the shapes seen in real landscapes.

Admittedly, the algorithm that generated these specimens is inexact, at best. Von Schelling's calculations call for taking a limit as the step size goes to zero, and my simulations are nowhere near that limit. Also, it should be noted that individual walks can be made more like the average walk by reducing the standard deviation of the angular distribution—by squeezing the randomness out of the random walk. Still, as von Schelling noted, it's far from self-evident that the typical path will ever come to resemble the average path.

Shifting Sands

Let me return to the question with which I began this column: Why doesn't a river just take the shortest path to the sea? From the point of view of a drop of water moving with the current, there is no paradox in the existence of meanders. The water follows the local gravitational gradient, which always points downriver. But how does that gradient get twisted into such tortuous shapes? The issue is not how the channel guides the river but how the river carves the channel.

Simple curves, random walks and optimization principles may not be enough to answer such questions. We may need to get into the nitty-gritty of erosion, deposition and sediment transport. Leopold dealt with these matters in his accounts of meanders, as others had before him, going back a century or more. The basic idea is that once a bend has formed, differential erosion and deposition tend to exaggerate it. Water flows more rapidly near the outer bank, which therefore tends to wash away. Meanwhile the slower current near the inner bank drops its load of sediment, forming a "point bar." The net effect is to shift the channel in a way that widens the bend.

Computer simulations of this process have produced some very realistic-looking meanders. The models are detailed and elaborate, incorporating dozens of subtle effects—cross-channel currents, graded sediment, variations in bank erodibility. The output reproduces not only the static form of natural meanders but also their evolution.

Is that the answer, then: What we need to understand meandering is not abstract mathematics but a bucket of sand and silt? I would be willing to leave it at that but for one extraordinary fact: Rivers meander even when they carry no sediment, and even when they have no banks! Meltwater streams atop glaciers, with no sand to deposit in point bars, meander much like other rivers. And the Gulf Stream, flowing unconfined in the open ocean, also meanders in a way remarkably like that of a river carving its way through continental alluvium. It appears there may be some principle at work that transcends the particular dynamics of the erosion-deposition cycle.

Reviewing the state of meander studies in 1998, David Knighton of the University of Sheffield concluded, "There is no general agreement as to how or why streams meander." That's a bit of a step backward from where I began—with admiration for Luna Leopold's simple and elegant theory. But I haven't lost my admiration, or given up on simple and elegant explanations. Although meanders have so far wriggled out of my grasp, I still think the universe will turn out to be a comprehensible place.

© Brian Hayes