The Secret History of Gravitational Waves
By Tony Rothman
Contrary to popular belief, Einstein was not the first to conceive of gravitational waves—but he was, eventually, the first to get the concept right.
Contrary to popular belief, Einstein was not the first to conceive of gravitational waves—but he was, eventually, the first to get the concept right.

On February 11, 2016, ecstatic scientists worldwide basked in the announcement that the Laser Interferometer Gravitational Wave Observatory (LIGO) had detected gravitational waves produced by the merger of two black holes more than a billion light years from Earth. Many members of the cosmological community had waited, literally, most of their lives to hear that announcement. At least one has confessed that his eyes welled with tears.
LIGO’s achievement rightly captured the public’s imagination, and since that historic February day the newborn science of gravitational wave astronomy has remained in the news. Additional detections have been announced on a regular basis; most spectacularly, on August 17, 2017, the facility recorded gravitational waves produced by the collision of two neutron stars. In recognition of LIGO’s triumph, the project leaders were awarded the 2017 Nobel Prize in Physics. Along the way, each press release or media report has been accompanied by a formulaic nod, intended to provide the ultimate seal of approval on the findings: “Gravitational waves were first predicted by Albert Einstein a century ago on the basis of his general theory of relativity.”
That sound-bite may be helpful in selling a complicated story, but it erases essentially the entire historical context. Contrary to conventional wisdom, Einstein was not the only physicist in the early 20th century attempting to create a modern description of the gravitational field. With hindsight, we can say that virtually any field theory of gravity will predict gravitational waves, so long as it obeys the fundamental precept that such disturbances must propagate at finite velocity.
Furthermore, Einstein himself did not immediately arrive at a definitive result. After completing his general theory of relativity in 1916, he initially dismissed the idea of gravitational waves, and his first paper dedicated to the subject got the description very wrong. Einstein soon hit on the correct formulation, but two decades later he rejected the physical reality of gravitational waves, and he remained skeptical about them for the rest of his life.
Like most scientific concepts, that of gravitational waves emerged over many years, through the work of numerous architects. Those architects were neither naïfs nor plagiarists. They were merely scientists working in sometimes friendly and sometimes not-so-friendly competition, seeking to solve a long-recognized problem. In those efforts, they may well have believed they were being less revolutionary than evolutionary.

LIGO/Virgo/NASA/Leo Singer; Milky Way image: Axel Mellinger.
To begin at the beginning: When in 1687 Isaac Newton introduced his law of gravity, it described in a single equation the gravitational attraction between any two objects. The striking thing was, whereas most previously known forces arose when two objects pushed or pulled each other via physical contact, Newton’s gravitational force evidently operated across great voids of empty space. Such “action at a distance” disturbed fellow philosophers, who demanded to know how gravity was transmitted from the Earth to the Moon. Newton’s celebrated reply was “Hypotheses non fingo,” which loosely translates as, “Guys, I haven’t the faintest idea, but the equation works.”
That evasion apparently failed to satisfy Newton himself, who had already written to the English theologian Richard Bentley, “that one body may act on another at a distance through a vacuum, without the mediation of anything else…is to me so great an absurdity, that I believe no man, who has in philosophical matters a competent faculty for thinking, can ever fall into it.” From a modern perspective, the more disturbing aspect of Newton’s law is that it assumes the gravitational force is transmitted instantaneously. If the Moon suddenly disappeared, lunar tides would vanish with no delay.
Over the next two centuries, such concerns gave rise to the notion of a space-filling field, which can be imagined as the medium that transmits the message. More precisely, a field is a continuous and continuously varying plane of action through which disturbances propagate, eliminating the conceptual knot of “action at a distance.” Today no one doubts the reality of fields; anyone who has sprinkled iron filings on a piece of paper above a bar magnet has perceived a field pretty directly. Back then, the existence of fields was less obvious.
By the 1840s, however, the creators of hydrodynamics were treating fluid properties—velocity, density, pressure—as fields. Hydrodynamic concepts, in turn, soon provided the basis for the 19th century’s most celebrated field theory, the electromagnetism of James Clerk Maxwell. By treating electricity and magnetism as fields, the Scottish mathematical physicist not only demonstrated that the two were intimately connected, but also showed that electromagnetic fields can propagate as waves at the velocity of light. The conclusion was nearly inescapable: Light itself was an electromagnetic wave.
The implications of this discovery for the understanding of gravity were not lost on Maxwell. In his 1865 “The Dynamical Theory of the Electromagnetic Field”—the very paper in which he deduced that electromagnetic waves travel at light speed—he wrote: “After tracing to the action of the surrounding medium both the magnetic and the electric attractions and repulsions [oscillations]…we are naturally led to inquire whether the attraction of gravitation, which follows the same law of the distance, is not also traceable to the action of a surrounding medium.” In other words, he wondered, can one think of gravity as being propagated by a field?
Heaviside set down the gravitational analogue of Maxwell’s equations and showed that they produce waves traveling at a finite velocity.
Maxwell’s challenge was taken up in 1893 by the brilliant English physicist and electrical engineer Oliver Heaviside. Writing in The Electrician, the leading electrical journal of the time, Heaviside set down the gravitational analogue of Maxwell’s equations and showed that they produce waves traveling at a finite velocity. One hesitates to make rash claims, but Heaviside’s article may well have been the world’s first serious scientific paper to treat gravitational waves.
In a sequel, Heaviside considered how a gravitational field changes when the attracting bodies are moving and the field propagates at finite velocity. He found that the changes in the field would produce small perturbations in the orbital motion of the Sun. The nondetection of such perturbations set an upper limit on the speed of gravity, suggesting it is probably the same as the speed of light. Heaviside’s calculations predated even special relativity and so could not give precisely correct answers, but within that restriction they are eminently sound.
By then, however, the idea that gravity might be propagated at a finite velocity was hardly novel; the French mathematician Pierre-Simon Laplace had enlisted such a hypothesis as early as the 1770s. Nor was Heaviside alone in his attempts to exploit gravity’s speed limit. In 1901, Jonathan Zenneck— remembered now as an important radio pioneer—wrote an article on gravitation for a German encyclopedia. In it, he surveyed multiple proposals to modify Newtonian gravity to make it more closely resemble Maxwellian electromagnetism, which by then many natural philosophers believed was the basis of all physics.
Heaviside’s work does not appear to have made much of an impression on Zenneck, who relegates it to a footnote, but Zenneck does describe the work of several other contemporaries who likewise assumed that gravitational effects propagated at the speed of light. Some proposals were designed to explain the notorious riddle of Mercury’s perihelion shift: The longitude of the planet’s closest approach to the Sun kept advancing by the small but mysterious angle of 43 seconds of arc per century, and no known Newtonian forces could account for it.
One modified theory of gravity, devised by the German physicist Paul Gerber (1854–1909), astoundingly gave the correct answer for Mercury’s movements. However, none of the schemes mentioned in the encyclopedia article—including Gerber’s—resembled a modern relativistic theory of gravity. A forlorn Zenneck lamented, “All attempts to connect gravitation with other phenomena in a satisfying way are to be regarded as unsuccessful or as yet not adequately established.”

ESO/L. Calçada/M. Kornmesser, University of Cambridge Digital Library, Wikimedia Commons, Robert Bein/AIP Emilio Segrè Visual Archives, Max Planck Institute for the History of Science, Leiden Observatory Archives, Liber Amicorum H.G. van de Sande Bakhuyzen
With his publication of the special theory of relativity in 1905, Einstein completed Maxwell’s unification of electricity and magnetism by showing that the two fields were really one. Special relativity was founded on two immortal postulates. First, that experimenters must always get the same result for any experiment in any frame of reference (that is, no matter how fast they are moving relative to each other), as long as they are moving at constant velocity. Second, that observers will always measure the speed of light to have the same value, 300,000 kilometers per second, regardless of their motion. These postulates led to the conclusion that no information—not even the propagation of gravity—can travel faster than light, and they demanded a thorough modification of Newtonian physics.
During the same months that Einstein was working on special relativity, the French polymath Henri Poincaré was independently writing up his own researches along similar lines. “On the Dynamics of the Electron,” Poincaré’s 1905 paper, contains much the same mathematical content as Einstein’s, but he failed to ground his ideas on the two key postulates, which is why Einstein receives the credit for relativity. Presciently, the last section of Poincaré’s paper is titled “Hypothesis on Gravitation.” In it, Poincaré attempted to understand how Newtonian gravity between moving bodies should be modified by the Lorentz transformations, equations which describe how the electromagnetic field changes to observers moving at different velocities.
Much as Heaviside had done (but this time in the context of a relativistically correct framework), Poincaré assumed that the gravitational force propagates at the speed of light; therefore, there will be a time lag—called a retardation by physicists—between any change in gravity and the effect. Such changes, Poincaré explicitly stated, are propagated by gravitational waves (ondes gravifiques), although he does not elaborate on their form. Poincaré was more correct in his assumptions than he perhaps realized: Retardation is the only thing a field theory needs to produce gravitational waves.
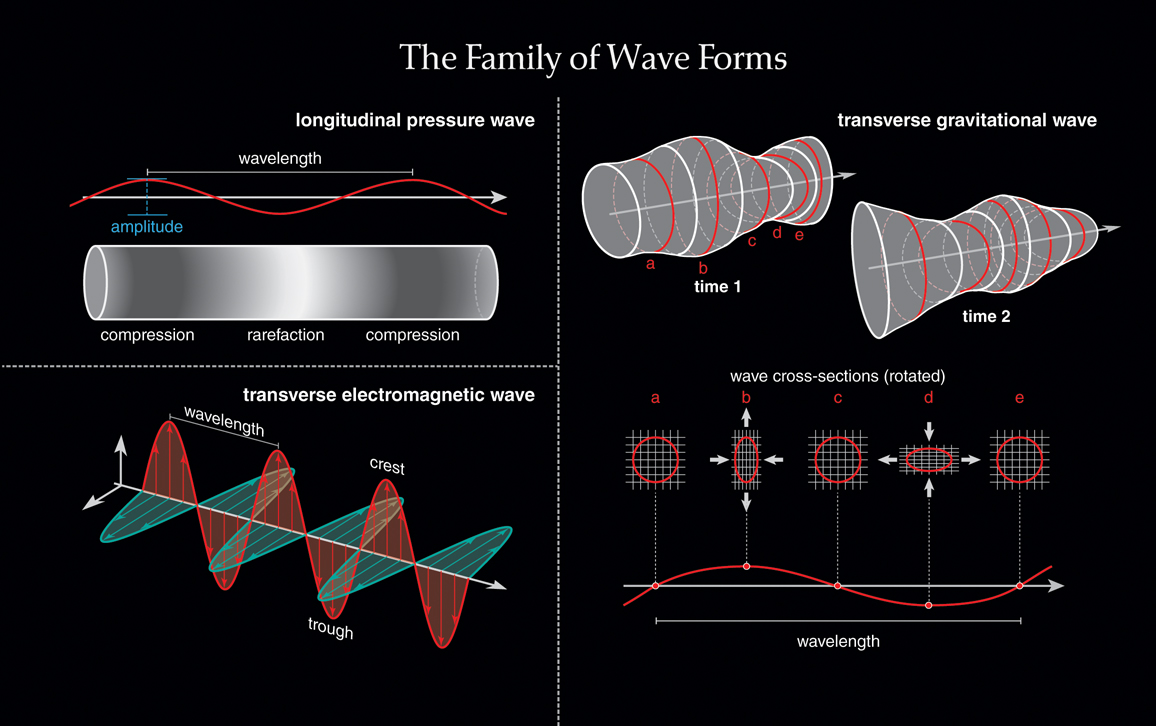
Illustration by Barbara Aulicino
Within a few years, Einstein understood that gravitation could not be consistently incorporated into his special theory of relativity. The reason for that incompatibility lay in what Einstein called the “luckiest thought” of his life: the principle of equivalence. In 1907, he realized that there is no experimental way to distinguish an acceleration due to motion from an acceleration due to a gravitational field. In the classic example, a rider in an elevator cannot tell whether the elevator is sitting still on Earth or accelerating at a rate of 9.8 meters per second squared (that is, 1g) in outer space. The two effects are exactly equivalent. Put another way, all masses, regardless of their nature or composition, fall at the same rate in a gravitational field.
Special relativity deals only with bodies moving at constant velocity, not accelerating ones. The principle of equivalence showed Einstein that special relativity therefore could not be extended to explain gravity, as some of his competitors were attempting to do. Conversely, a theory that could explain accelerating objects would necessarily give Einstein a new theory of gravity as well.
In a 1911 paper, Einstein took the first steps in that direction by using equivalence to demonstrate that photons must gain energy as they fall toward a gravitating body and lose energy as they climb away from it. Light emitted by a massive body is stretched, resulting in a gravitational redshift, a phenomenon inconsistent with gravity-free special relativity. Clocks at different heights above a gravitating body likewise tick at different rates. As a result—or so Einstein initially believed—the speed of light must change in a gravitational field.
A variable speed of light did not survive in general relativity, but Einstein’s thinking had an immediate impact on Max Abraham. Abraham (1875–1922) was a tragic figure in early 20th-century physics, remembered largely as having fallen on the wrong side of history by bitterly opposing both Einstein’s special and general theories of relativity. During his lifetime, though, he was widely acknowledged as a leading physicist, especially in matters of electromagnetism, which he believed was the foundation of all reality.
In 1912, Abraham published a theory of gravity in which he modified special relativity (somewhat inconsistently) to include a variable speed of light along the lines Einstein had proposed. Abraham’s scheme was what we call a scalar theory. A scalar is merely a quantity (temperature, for example) that is entirely characterized by its magnitude. Once you’ve said that the temperature in the living room is 20 degrees Celsius, you’ve said all there is to say about it. However, the living-room temperature may be 20 degrees while the bedroom temperature is 18 degrees, and both values certainly change between dawn and sunset. Thus the house temperature represents a scalar field varying in space and time.
Abraham’s scalar was the gravitational potential energy of the field itself. A scalar theory of gravity is simpler than Maxwell’s electromagnetism, which is termed a vector theory because the electric and magnetic fields behave as vectors: They have magnitudes but also point in specific directions. Just as an accelerating electric charge produces electromagnetic radiation, an accelerating mass should emit gravitational radiation. In Abraham’s theory, an accelerating mass inarguably did just that, and he discussed gravitational radiation extensively early in 1912 at a conference in Italy—a lecture which later that year was published in the journal Nuovo Cimento. It may well have been the world’s second paper devoted to gravitational waves.
Abraham realized that the waves produced by his theory were longitudinal—that is, the field oscillates along the direction of the propagation of the wave, just as air density fluctuates in the same direction in which a sound wave propagates. By contrast, electromagnetic waves are transverse, meaning that the waves vibrate in a direction perpendicular to the direction of propagation. It turns out that gravitational waves are transverse as well, so Abraham didn’t get it exactly right. But a scalar-wave description is often enlisted even today by teachers introducing gravitational waves to students, and in doing so we are following Abraham rather than Einstein.
Even as Abraham discussed gravitational waves in relation to electromagnetic waves, he understood that the comparison was not entirely legitimate. By far the dominant type of electromagnetic radiation is dipole radiation, which is emitted when a single electric charge (or collection of charges) accelerates. One might reasonably think that if a single mass were accelerated it should analogously emit gravitational dipole radiation. However, Abraham maintained that the law of conservation of momentum would forbid a single mass from accelerating without a second mass accelerating in the opposite direction. That correct conclusion forbade the existence of any gravitational dipole radiation, leading him to declare that the hope to observe gravitational waves “is futile.”
Along the way, though, Abraham had another gravitational insight: He anticipated the German physicist Karl Schwarzschild by predicting what we now call the “Schwarzschild radius”—the size of the event horizon of a black hole. The event horizon is the place of no return that separates the interior of the black hole from the rest of the universe, and it is still an area of intense theoretical investigation.
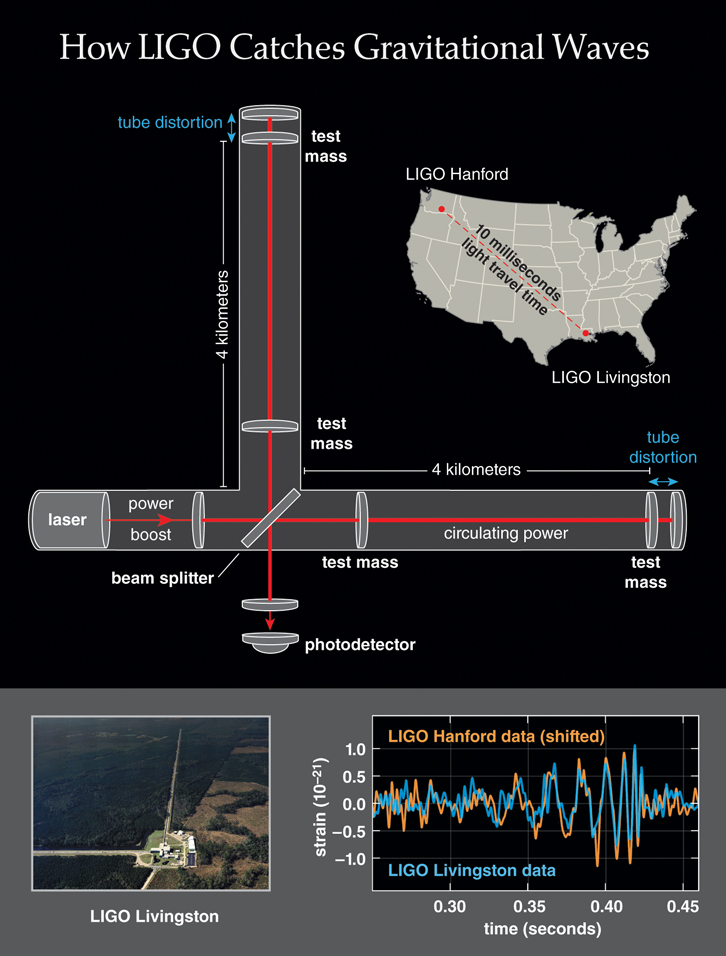
Illustration by Barbara Aulicino
Einstein and Abraham were not alone in their meditations and arguments about the nature of gravitation. The German physicist Gustav Mie (1868–1957) also contributed to the scientific ferment. Mie is today remembered primarily for his theory of light scattering off spherical particles. A century ago, though, his overarching goal was to create a unified field theory that explained electromagnetism, gravitation, and matter by means of a single “world function” from which all else followed.
Mie’s work was so vast that apparently few people noticed that chapter five of his opus on unified field theory contains a theory of gravity. His proposal retains a constant speed of light, and with it the principles of special relativity, but in many respects it is quite similar to Abraham’s. It is a scalar theory, and, like Abraham’s, it predicts longitudinal gravitational waves propagating at the speed of light. Mie does not appear to realize that gravitational dipole radiation is forbidden, but he does conclude that “The gravitational radiation emitted by oscillating electrons (or by any oscillating mass particle) is so extraordinarily weak that it is unthinkable ever to detect it by any means whatsoever [Mie’s italics].” In his view, “if one could ever prove the existence of gravitational waves, the processes responsible for their generation would probably be much more curious and interesting than even the waves themselves.”
Einstein—not yet world-famous, but already a towering figure in physics—gave short shrift to Abraham and failed to mention Mie at all in a 1913 lecture, “On the Present State of the Problem of Gravitation,” presented at the 85th Naturforscherversammlung (Congress of Natural Philosophers) in Vienna. That omission led to a lively exchange during the discussion afterward. Mie complained about being overlooked, while admitting that “my theory is tucked away in a comprehensive work on the theory of matter in general, and for that reason my investigation probably escaped Mr. Einstein’s notice.”
“No, no,” Einstein interjected jovially (we hope), showing that he was at least aware of Mie’s work. In his full response, Einstein admitted that he had not read Mie “as attentively as perhaps would have been good, but I had not the slightest intention of disparaging Mie’s theory by not mentioning it.” But Einstein does not retreat: He didn’t mention Mie’s work, he explains, because in it all masses do not fall at the same rate in a gravitational field; Mie violated the principle of equivalence. Consequently, “it would have been illogical of me to start from certain postulates and then not adhere to them.” As for Abraham, Einstein stated that his theory violated the basic premises of relativity.
Einstein displayed far more appreciation for the work of the young Finnish physicist Gunnar Nordström (1881–1923), and spent a large portion of his lecture explicating his theory. Nordström is remembered among relativists as the independent codiscoverer, along with the German engineer Hans Reissner, of the “Reissner-Nordström metric.” That metric was an early solution to the equations of general relativity that, like the more famous solution discovered by Karl Schwarzschild, describes spacetime around a black hole—except that in the Reissner-Nordström case, the black hole is electrically charged.
A friendly competitor and sometime collaborator of Einstein’s, Nordström—observing the ongoing clash between Einstein and Abraham—created two different gravitational theories in 1912–1913, the second of which Einstein showcased in Vienna. Textbooks and popular accounts universally claim that Einstein was the first to equate the geometry of a flexible spacetime (placed on the left side of his field equations) with the matter affecting that geometry (placed on the right), demonstrating the revolutionary idea that mass and geometry are intimately connected. In truth, that honor belongs to Nordström, who had created the first relativistically consistent field theory of gravity.
Like the theory of general relativity that was to come, Nordström’s theory allowed matter to curve spacetime, albeit in a mathematically more restrictive sense. It was still a scalar theory, like Abraham’s had been, but in it the speed of light remained strictly constant and the principle of equivalence was respected. All in all, Nordström’s formulation resembles Einstein’s general relativity closely enough that it is still occasionally enlisted for illustrative purposes because it is much simpler.
In available documents, Nordström did not explicitly discuss gravitational waves. His theory did unquestionably predict them, however; his field equation is precisely an equation for transverse gravitational waves. The main problem with Nordstöm’s theory was that it turned out to be wrong. It incorrectly predicted that light would go undeflected by the Sun’s gravity, and it gave the wrong direction for Mercury’s perihelion shift. Whether Nordström remained mute on the subject of gravitational waves because of Abraham’s conclusions is unclear. What is clear is that the time was ripe for general relativity.
In Einstein’s monumental 1916 paper announcing the completion of general relativity, one of the first things he did was to return to the problem of Mercury’s perihelion—and he got the orbital shift exactly right. There was no mention of gravitational waves in the paper, however. Strangely, it appears that Einstein did not believe in them at the time. On February 19, 1916, he replied to a letter from Schwarzschild, which has not survived, but Einstein’s response makes fairly clear his feelings about the subject: “There are no gravitational waves analogous to light waves.”
Regardless, within a few months Einstein produced his own paper on the topic, “Approximate Integration of the Field Equations of Gravitation.” In it, he gave no more evidence than his predecessors that he believed gravitational waves would ever be detected. He also arrived at the erroneous conclusion that an oscillating spherical mass would produce gravitational radiation in a form known as monopole radiation, something that is forbidden even in electromagnetism.
Two years later, in 1918, Einstein opened his second paper on gravitational waves with the remark that he was returning to the subject because “my former presentation is not sufficiently transparent and, furthermore, is marred by a regrettable error in calculation.” That is, to be charitable, putting it mildly. In general relativity, gravity determines the fabric of spacetime, which resembles the surface of a boundless trampoline, capable of being stretched in all directions. Whereas Newton required one equation to describe the force of gravity, Einstein required 10 to describe the entire field. The mathematical objects required to do this are called tensors (loosely, they are matrices as opposed to vectors), which makes general relativity more complicated than either Maxwell’s vector theory of electromagnetism or the scalar theories of gravity.
The tensors of relativity embody the coordinates you are using to describe the problem at hand. During any analysis, it is easy to confuse what is happening according to your coordinates with what is taking place in the physical world. In one coordinate system, a wave may appear to be rippling across space, whereas in another coordinate system space may appear absolutely flat. Einstein had fallen into this trap, more or less misplacing the location of gravitational energy. In his 1918 paper, Einstein credits Nordström with putting him on the right track. Rectifying his error, Einstein finally arrives at the correct formula for gravitational radiation. Even now, though, he does not speculate on whether such radiation is real or could ever be detected. For two decades, that was his last word on the subject.
As an interesting aside, in his correspondence with Einstein, Nordström referred to the black hole solution not as the Schwarzschild solution but as the Droste solution. Johannes Droste (1886–1963), a graduate student of the Dutch physicist Hendrik Lorentz, discovered it independently of Schwarzschild within the same few months.
Einstein’s 1918 paper on gravitational waves stands as the foundation of the subject as we know it today. Yet the confusion didn’t remotely end there. To arrive at his 1918 results, Einstein simplified general relativity’s equations. When he revisited the topic in a 1936 paper with Nathan Rosen, his assistant at the Institute for Advanced Study in Princeton, Einstein argued that the theory’s fully developed equations proved that true gravitational waves could not exist after all.
As it turned out, Einstein and Rosen were repeating the old mistake of using bad coordinates. American physicist Howard P. Robertson soon corrected the error, but Einstein’s lingering skepticism toward gravitational waves largely impeded research in the field until after his death in 1955. Not until the late 1950s did the combined work of physicists Hermann Bondi, Felix Pirani, Ivor Robinson, and Andrzej Trautman finally establish the reality of gravitational waves in the full theory of general relativity. Even then it took another 60 years of theoretical, experimental, and instrumental progress before physicists were able to directly detect gravitational waves and explore their real-world properties.
Einstein’s skepticism largely impeded research in the field until after his death.
The August 2017, observation of near-simultaneous gravitational and gamma-ray signals from a pair of colliding neutron stars 130 million light years away proved that, as expected, gravitational waves propagate at the speed of light. Also, like electromagnetic waves, they are transverse, oscillating perpendicularly to the direction of their propagation. But at a fundamental level, the two types of waves are completely different.
Gravitational waves are essentially tidal disturbances that ripple across space. As they pass an object, they stretch it in one direction and squeeze it in another, just as lunar tidal forces do to the Earth. They are incredibly weak both because of the inherent weakness of the gravitational force and because gravitational waves are of a type technically known as quadrupole radiation, which is much more feeble than the dipole radiation characteristic of electromagnetism. The strongest gravitational disturbance yet detected—which also happened to be that first one, celebrated in 2016—was so slight that it displaced the mirrors at LIGO by just one ten-thousandth of the diameter of an atomic nucleus. Such was the level of precision needed to quantify the phenomenon that so many theorists spent so many years formulating and debating.
The public perception of Einstein today is that he singlehandedly solved the great physical riddles of the age. If you were a scientist attending the 1913 Vienna conference, though, you might think that our perception of historical reality has suffered some distortion across space and time. Inhaling the pipe smoke as you listen to the squabbles, you might well conclude that Einstein was indeed the preeminent mind in sight, his proposals bolder and more profound than those of his competitors. Yet, you might also sit back and say to yourself, “Those other fellows are no slouches either.”
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.