The Ultimate Mouthful: Lunge Feeding in Rorqual Whales
By Jeremy A. Goldbogen
The ocean's depths have long shrouded the biomechanics behind the largest marine mammals' eating methods, but new devices have brought them to light
The ocean's depths have long shrouded the biomechanics behind the largest marine mammals' eating methods, but new devices have brought them to light

DOI: 10.1511/2010.83.124
A hungry fin whale dives deep into the ocean to perform a series of rapid accelerations with mouth agape into a dense prey patch. On each of these bouts, or lunges, the whale engulfs about ten kilograms of krill contained within some 70,000 liters of water—a volume heavier than its own weight—in a few seconds.

Randy Morse, GoldenStateImages.com
During a lunge, the whale oscillates its tail and fluke to accelerate the body to high speed and opens its mouth to about 90 degrees. The drag that is generated forces the water into its oral cavity, which has pleats that expand up to four times their resting size. After the whale’s jaws close, the sheer size of the engulfed water mass is evident as the body takes on a “bloated tadpole” shape. In less than a minute, all of the engulfed water is filtered out of the distended throat pouch as it slowly deflates, leaving the prey inside the mouth. Over several hours of continuous foraging, a whale can ingest more than a ton of krill, enough to give it sufficient energy for an entire day.
Years ago, Paul Brodie of the Bedford Institute of Oceanography described the feeding method of fin whales as the “greatest biomechanical action in the animal kingdom.” This extreme lunge-feeding strategy is exhibited exclusively by rorquals, a family of baleen whales that includes species such as humpback, fin and blue whales. Like all baleen whales, rorquals are suspension filter feeders that separate small crustaceans and fish from engulfed water using plates of keratin—the same protein that forms hair, fingernails and turtle shells—that hang down from the top of their mouths. By feeding in bulk on dense aggregations of prey, baleen whales can support huge body sizes—they count among their numbers some of the largest animals that have ever lived. Rorqual lunge feeding is especially unusual not only with respect to the tremendous size of the engulfed water mass, but also in the underlying morphological and physical mechanisms that make this extraordinary behavior possible.
Because of the logistical difficulties in studying rorqual lunge feeding deep in the ocean, our knowledge of this ingestion process, until recently, has been limited to observations made at the sea surface. Over the past several years, my colleagues and I have made significant advances in understanding how lunge feeding works. Our collective effort has been motivated by unique data generated by digital tags attached to the backs of lunge-feeding rorquals. These tags have enabled us to quantify the particular body movements that rorquals undergo during a lunge-feeding event. With these data we have been able to determine the physical forces at play during engulfment and also to estimate the magnitude of the water mass taken in. In doing so, we have confirmed many predictions previously made by early investigators that were based only on anatomical knowledge and sea-surface observations. Moreover, our analyses have uncovered new engulfment mechanisms, which, in turn, have led us back to studying the remarkable morphological adaptations that drive the lunge-feeding process.
Our first insight into how lunge feeding works came in large part from the pioneering studies of August Pivorunas, Richard Lambertsen and Paul Brodie over the past several decades. Their investigations focused on the anatomical machinery that makes lunge feeding possible. Rorquals exhibit a complex suite of bizarre morphological adaptations in the head, mouth and throat. The head looks more reptilian than mammalian; its shape is a key characteristic required to meet the conflicting demands of engulfment and locomotion. A rorqual must have a large, distensible mouth in order to engulf a large volume of water—but it also has to be able to contract and tighten back into the body to maintain a streamlined shape for low drag and efficient steady swimming, particularly during long dives or long-distance migration.

Photograph courtesy of the Shetland Museum and Archives.
In the larger rorqual species, the skull and mandibles are truly massive, making up nearly 25 percent of the body. The mandibles are connected to the base of the skull through giant pads of a dense, elastic matrix of fibers and cartilage that are infused with oil. This type of jaw joint is unique to rorquals, and possibly also to the closely related gray whale. These specialized jaw joints are flexible linkages between the skull and mandibles, which permits the jaws to open to nearly 90 degrees. Such a feature is required so the whales can engulf as much water as possible during a lunge: Although the mouth area is very large, the proportion of that area directed toward the prey is determined by the gape angle between the skull and jaws.
The rorqual skull also possesses a third jaw joint, the mandibular symphysis, which connects the mandibles at the center of the lower jaw. In some mammals this linkage is fused, but in rorquals it also has a fibrocartilage composition that enhances its flexibility. With this third, very flexible jaw joint, the strongly curved mandibles are able to rotate outward and increase the area of the mouth. Mandibular rotation is consistently observed in lunge-feeding rorquals at the sea surface, and also in post-mortem specimens when the muscles that hold the mandibles in place release and allow them to sag open.
By having a kinetic skull with specialized jaw joints, rorquals enhance mouth area and increase the rate of water flow into the oral cavity. This rapid influx of water is facilitated by a most unusual mechanism: a tongue that can invert and form a capacious oral sac that accommodates the engulfed seawater on the ventral side of the body. The rorqual tongue is extremely flaccid and deformable. Although it has some distinct structure reminiscent of a typical mammalian tongue, it is weakly muscularized and composed largely of elastic fatty tissue. A floppy, loose tongue can be easily inverted when water rushes into the oral cavity (also called the buccal cavity). Moreover, there is a specialized intramuscular space, called the cavum ventrale, located between the bottom of the tongue and the walls of the buccal cavity, which extends all the way down to the whale’s belly button. During engulfment the tongue inverts into the cavum, retreating through the floor of the mouth and back towards the belly button, forming the large oral sac that holds the incoming seawater.
The extreme distension of the buccal cavity during engulfment presents a problem for the walls of the body, which in cetaceans is composed of stiff blubber and firm connective tissue. All rorquals have a distinct series of longitudinal furrows in the ventral blubber that span nearly half of the whale’s body length, from the snout to the belly button. In fact, the name “rorqual” comes from the Norwegian word röyrkval, meaning “furrow whale.” This ventral groove blubber (VGB) consists of tough ridges separated by deep channels of delicate elastic tissue; when viewed in cross- section, the VGB has an accordion-like architecture that could easily unfurl if the underlying muscle became relaxed. The tremendous engulfment capacity of rorquals is clearly dependent on this unique morphological design, and it turns out that the VGB is remarkable not only in its structure but also in its mechanical behavior.
The first major breakthrough in understanding the biomechanics of lunge feeding came in the late 1980s from some simple, yet elegant, experiments by Lisa Orton and Paul Brodie. The researchers obtained fresh samples of fin whale VGB from a whaling station in Hvalfjördur, Iceland and performed mechanical tests on the tissue to determine how much strain it could withstand for a given amount of stress. They found that the VGB and associated muscle layers could reversibly extend up to several times their resting length. This extraordinary extensibility was attributed to the vast amounts of elastin, a specialized elastic protein, found throughout the tissue, and the fact that the VGB unfolds like a parachute canopy in the absence of muscle tone.
The extensibility of the VGB is a key component of the engulfment apparatus because it provides the great capacity that is needed for a whale to envelop large amounts of water and prey. In addition, the amount of force that is required to sufficiently stretch the tissue provided an important clue as to how fast a fin whale must swim to successfully execute a lunge. As a rorqual accelerates and lowers its jaws, dynamic pressure is generated inside the oral cavity and applied against the floor of the mouth. In theory, the dynamic pressure alone could generate enough force to completely extend the VGB and inflate the buccal cavity, but only if the swimming speed is high enough. By approximating the inflated buccal cavity as a thin-walled cylinder, Orton and Brodie predicted that a lunge speed of 3 meters per second would be sufficient to maximally fill a fin whale’s buccal cavity. This prediction seemed consistent with sea-surface observations, but there was really no way to accurately measure swim speed during a lunge until very recently.

Image from globalfiredata.org.
Nearly two decades after Orton and Brodie’s study, the opportunity came to test their predictions by examining the motion, or kinematics, of rorqual lunge-feeding in the natural environment. Bill Burgess of Greeneridge Sciences developed a high-resolution digital tag that could be temporarily attached to the backs of whales as they surface to breathe. The tags, equipped with suction cups for attachment and a flotation device for retrieval, contained a variety of sensors, including a hydrophone, a pressure transducer and an accelerometer. The data from these tags provided a short glimpse into the underwater behavior of rorquals, including body orientation, the times when the whale was swimming versus when it was gliding, and dive depth. The application of these tags, using a long fiberglass pole, is not a trivial task—it requires many years of experience at sea and typically a coordinated effort between a large support vessel and a smaller tagging boat.
The tagging operations were led by John Calambokidis and Greg Schorr from the Cascadia Research Collective in Olympia, Washington, and Erin Oleson of the Scripps Institution of Oceanography. For the past seven to eight years, tagging studies were conducted every summer at various locations off the coast of California and Mexico. The tag data showed that many rorquals made consecutive deep dives, in some cases up to 300 meters in depth. At the bottom of these deep dives, the data showed a series of wiggles or undulations. Each wiggle was accompanied by an intense bout of active swimming strokes and a concomitant decrease in water flow noise, which indicated a rapid decrease in speed that is typically seen during lunges at the sea surface.

Top photograph courtesy of Nick Pyenson. Illustrations at bottom by Tom Dunne.
Although these data were suggestive of lunges at depth, direct evidence came from another type of suction-cup tag: National Geographic’s Crittercam, conceived and developed by Greg Marshall. The video camera within Crittercam was equipped with an infrared light, for the dark conditions during deep dives, and also a time-depth recorder. The video footage shows the whale swimming through dense fields of krill at the bottom of deep dives. The images from one Crittercam deployment shows the whale’s lower jaws dropping, followed by a decrease in flow noise, and then an expansion of the ventral groove blubber. This provided visual confirmation of the behavior that we had interpreted from the data recorded by our digital tags: several consecutive lunges at the bottom of deep foraging dives.

Photograph by Sherwin Cotler, Cascadia Research.
After more analyses, we realized that we could use the level of flow noise recorded by the digital tag’s hydrophone to calculate the whale’s swimming speed throughout each foraging dive. This “flow-noise speedometer” revealed just how rapid the changes in speed were during a lunge. Amazingly, the maximum lunge speed recorded for fin whales was 3 meters per second, precisely the flow speed that Orton and Brodie had predicted to be enough to passively inflate the buccal cavity. Furthermore, the speed data revealed a rapid deceleration of the body even while the whale continued to swim actively, an indication that the whale was experiencing very high drag as it opened its mouth wide. The kinematic data from the tags, it turns out, held the key to determining not only how much drag is incurred, but also how much water the whale engulfs.
As a rorqual lowers its jaws and presents the inside of its mouth to oncoming flow, water that is rushing into the mouth will expand and distend the throat pouch. Such a reconfiguration represents a major departure from the whale’s normal sleek, well-streamlined body profile. The result is predictably high drag as flow is directed around the mandibles and distended buccal cavity, which robs momentum from the whale and causes the body to decelerate rapidly. The size and shape of the mandibles, therefore, has a great influence on how much drag is experienced during a lunge. Because the mandibles determine the size of the mouth, they also largely determine how much water is engulfed.
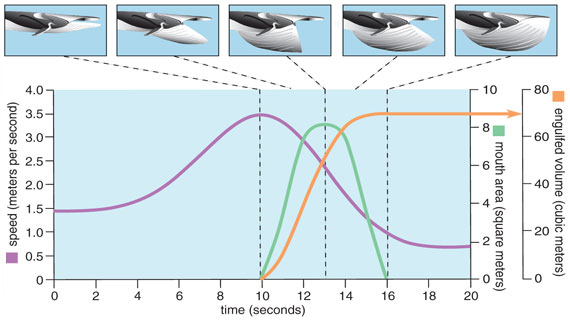
Recognizing the effects of skull and mandible shape on the mechanics of engulfment, Nick Pyenson of the Smithsonian Institution, Bob Shadwick of the University of British Columbia and I set out to measure as many museum specimens as possible. By integrating our morphological measurements with the kinematic data obtained from the tags, we were able to estimate how much water is engulfed during a fin whale lunge. When the jaws were open to maximum gape, for example, our calculations suggested that the buccal cavity was filling at a rate of approximately 20 cubic meters per second. At the end of a lunge that lasted six seconds, the accumulated engulfed water mass was about 60 tonnes, which again supported the prediction made by Paul Brodie in 1993. The engulfed water mass is about the size of a school bus, a truly enormous amount. The magnitude of the engulfed water is also colossal relative to the whale, whose own body mass weighs in at around 45 tonnes.
By engulfing a volume of water that is greater than its own body mass, the whale necessarily incurs tremendous amounts of drag. The whale must do work against this drag, and this represents a major source of energy expenditure during a lunge. The work required for engulfment triples over the course of a lunge, whereas the drag increases approximately five-fold. One other important metric in the field of hydrodynamics, called the drag coefficient, is a measure of how streamlined an object is and how effective it is at decreasing drag. High drag coefficients are typical of poorly streamlined shapes, whereas low values indicate a highly streamlined shape. Our simple calculations suggested that, over the course of a lunge, the drag coefficient increases by more than an order of magnitude. Thus, a lunge-feeding rorqual undergoes an extreme transformation from a very well-streamlined body to one that is highly susceptible to drag. Interestingly, the maximum drag coefficients were very similar to those for parachutes, another inflating system. The analogy between inflating parachutes and lunge feeding is logical: Both systems must reconfigure in order to generate drag. In other words, parachutes need drag to inflate and slow down their cargo, whereas rorquals require drag to inflate the buccal cavity.
The realization that rorqual lunge feeding involves incredibly high amounts of drag led us to a most unlikely collaboration with Jean Potvin, a parachute physicist at Saint Louis University in Missouri. Together we developed a new, more detailed model of rorqual lunge feeding inspired by decades of parachute-inflation studies. For a given morphology and initial lunge speed, the model predicted what decrease in velocity to expect for a passively engulfing whale as it experiences drag. By comparing the model output to the empirical tag data, we could explicitly test particular engulfment mechanisms. The first question we asked was: Is a lunge-feeding whale just like an inflating parachute? If this were the case, a rorqual would inflate passively, and the flow-induced pressure that expands the buccal cavity would be met with little resistance because of the extremely compliant properties of the VGB.

Our simulation of passive engulfment in fin whales resulted in a poor match with the tag data because the body was simply not slowing down rapidly enough. In other words, there wasn’t enough drag to account for the rapid deceleration that we had observed in the tagged whales. This also meant that water was going into the mouth far too rapidly and, as a consequence, the buccal cavity reached maximum capacity halfway through the lunge (at about the point when the mouth was open to maximum gape). Maximum filling of the buccal cavity would occur because at some point the VGB cannot extend anymore. At that point in time, the entire engulfed mass would have to be immediately accelerated up to the instantaneous speed of the whale (2 meters per second), which would impose unrealistic forces on the walls of the buccal cavity. If the VGB was not strong enough to accommodate these excessively large forces, passive engulfment would cause catastrophic blow-out of the buccal cavity. If the VGB was strong enough to withstand these forces, the engulfed mass would rebound off the buccal-cavity wall and eject back out of the mouth before the jaws closed. In either scenario passive engulfment does not seem to be a feasible mechanism for fin whales. However, such a mechanism might still be possible for lunges involving lower gape angles and smaller engulfed volumes.
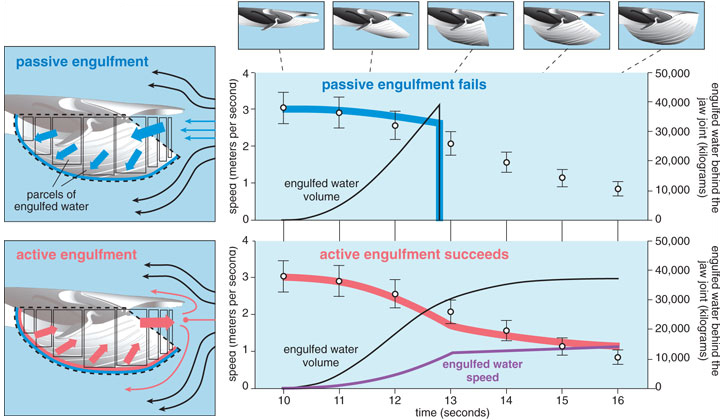
If passive engulfment is not possible, how do rorquals execute a lunge successfully? There are two key anatomical characteristics of the VGB that suggested a very different engulfment mechanism. First, we realized that there were several layers of well- developed muscle that adjoin tightly to the grooved blubber. Second, a study by Merijn de Bakker and his colleagues at Leiden University revealed that there were specialized nerves sensitive to mechanical stress, called mechanoreceptors, embedded within both the muscle and blubber layers of the VGB. These receptors were concentrated within each groove, which is precisely the region of the tissue that would stretch during engulfment. These two lines of evidence suggested that rorquals may be able to gauge the magnitude of the engulfed water mass from the amount of stretch sensed by the tissue and then generate enough force to slowly push the water forward. Such a mechanism is possible if the VGB muscles actively resist lengthening as they are stretched by the incoming flow. By virtue of Newton’s third law of motion, demanding equal action and reaction, the whale imparts its momentum to the engulfed water during this “collision”; the whale slows down as the engulfed water, which was initially at rest, speeds up, and eventually both of their speeds become more similar.
When we simulated this type of active engulfment, we found a good match to the velocity profile generated by the digital-tag data. The model output supported our hypothesis of active inflation in rorquals, a very different mechanism than what is observed in parachutes. But why would rorquals push water forward, out of the mouth, when they are trying to engulf it? Indeed, this shove from inside the buccal cavity generates even more drag compared to the case where water is just going around the body and the mouth, which is why the active engulfment simulation better matched the tag data.
Although it seems counterintuitive, pushing water forward during a lunge has some advantages. Gradually pushing water forward over the course of a lunge distributes the drag forces over a longer period. By smoothing out these forces over lengthier time scales, the peak drag forces experienced by the engulfment apparatus are effectively lower.
Another benefit associated with active engulfment is that it may increase the energetic and mechanical efficiency of filtration by the baleen. If the water is slowly pushed forward, the entirety of the engulfed water mass no longer has to be accelerated from rest. Moreover, because the trajectory of the engulfed water mass inside the buccal cavity is largely parallel to the filter surface of the baleen, rorquals could employ cross-flow filtration; this highly efficient filtration mechanism washes material perpendicularly across the filter surface to prevent clogging. It is used on an industrial scale (for example, in water purification, beer and wine production, and biotechnology processes) and has also been observed in suspension-filter-feeding fish. If such a mechanism exists in rorquals, as opposed to dead-end filtration where the filtrate gets stuck in the filter itself, it could be very effective at keeping small zooplankton from embedding in the baleen fringes. And further, if krill were to cake the baleen, how would a rorqual scrape it off with such a floppy, weakly muscularized tongue? Maybe one day technology will enable us to visualize the flow inside the mouth of a filtering rorqual and resolve the debate.
The high drag that is required for engulfment has major consequences for rorqual foraging ecology and evolutionary morphology. Not only must rorquals expend significant amounts of energy to accelerate the engulfed water mass, but the high drag also robs the whale of its kinetic energy, bringing the body to a near halt. As a consequence, the body must be reaccelerated from rest in order to execute the subsequent lunge. While holding its breath at the bottom of a dive, the whale must lunge over and over again, and this represents a high energetic cost. Thus, rorquals rapidly deplete their oxygen stores when foraging at depth and must quickly return to the surface to recover. The feeding costs related to high drag during lunge feeding effectively limit the amount of time a large rorqual can spend foraging at depth to about 15 minutes or so per dive. This short timeframe is unexpected because rorquals are so large, and in nearly all other air-breathing vertebrates, diving time usually scales up with increased size, due to a more efficient metabolism.
The severely limited diving performance of rorquals was first documented nearly a decade ago by Donald Croll and colleagues at the University of California, Santa Cruz. By attaching simple time-depth recorders to the backs of surfacing blue and fin whales, the researchers discovered that the whales’ foraging dives were much shorter than expected for their size. Furthermore, foraging dives that involved more lunges at depth resulted in more surface recovery time after each dive. Using these data, Croll’s research group was the first to hypothesize that, due to drag, there was a high energetic cost for each lunge. This hypothesis has been supported by several studies since then, not only for fin and blue whales, but for humpback whales as well.
Because maximum dive time is limited by these high foraging costs, rorquals are particularly dependent on dense aggregations of prey. In addition, it is predicted that a rorqual is morphologically designed to engulf as much water as possible per lunge, which may be why the buccal cavity extends halfway down the body to the belly button and why the jaws make up nearly a quarter of the body length. But why isn’t the engulfment apparatus even larger? What are the limits to engulfment capacity and how does it change with body size? These questions led me to a long- forgotten morphometric data set from the whaling literature, which allowed me to examine the consequences of scale and morphology on lunge- feeding performance.
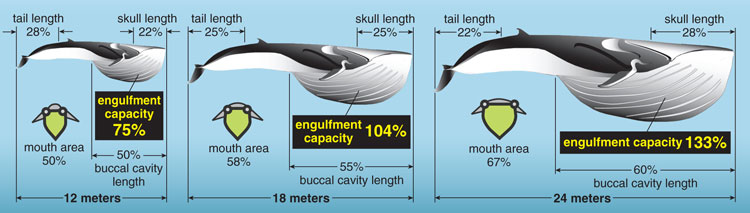
In an attempt to manage the whaling industry in the 1920s, the British government launched a series of expeditions called the Discovery Investigations in order to learn more about the natural history and biology of large whales in the Southern Ocean. One particular study focused on the body proportions of the two largest rorqual species, fin and blue whales. These species are not only some of the largest animals of all time, but what is often underappreciated is that they also exhibit a wide range in body size. For example, the length at weaning for fin and blue whales is approximately 12 meters and 16 meters, respectively, whereas the maximum size recorded for each species is 24 meters and 28 meters. These expeditions recorded morphometric data, some of which was related to the engulfment apparatus, for hundreds of fin and blue whales over this entire body-size range.
Tom Dunne
The authors of this study discovered a peculiar pattern related to body size: Larger whales had larger jaws and buccal cavities relative to body size. At the same time, the size of the posterior part of the body (the region from the dorsal fin back towards the tail fluke, or caudal peduncle) became relatively smaller. The researchers gave no possible explanations for these bizarre patterns of relative growth (also called allometry), probably because the data were collected before we knew how important morphology is in determining lunge-feeding performance. My colleagues and I amassed their complete data set for fin whales in order to estimate engulfment capacity as a function of body size. As we expected, the relative size of the engulfed water mass increased with body size, and this was directly due to the allometry of the engulfment apparatus.
But why did larger whales have relatively smaller caudal peduncles? We hypothesized that this relative shrinking of the tail could represent the cost of devoting all growth-related resources to the anterior region of the body. As rorquals grow, they become morphologically optimized to increase engulfment capacity. The skull becomes relatively longer and wider with body size, and therefore the area of the mouth that is devoted to engulfment is also relatively greater. In addition, the length of the ventral groove blubber system is also relatively longer in bigger whales, and this effectively increases the relative capacity of the buccal cavity. Given that many other large rorquals also exhibit the same patterns of relative growth, these allometric patterns may represent an adaptation (or exaptation) related to lunge-feeding performance.
The relatively smaller tail should not negatively affect swimming performance in larger rorquals because the actual fluke—the propulsion surface that generates the lift used for thrust—is generally proportional to body size. However, the enhanced engulfment capacity in larger whales does not come without a cost. The active nature of engulfment means that relatively larger water masses must be accelerated forward. Thus, larger rorquals will have to expend relatively more energy to successfully execute a lunge. Considering that high feeding costs limit dive time relative to other diving animals, such rapidly increasing costs for a lunge may limit diving capacity in larger rorquals even more. Such a consequence could be detrimental because sufficiently dense prey patches tend to be very deep. Theoretically, the rate of energy expenditure to feed will increase more rapidly with body size than the rate of energy gained from lunge feeding.
If this scenario is extrapolated to a hypothetical megarorqual that is much larger than a blue whale, we find that the whale would not be able to support its metabolism by lunge feeding. Similar problems associated with large body size were predicted by R. McNeil Alexander for baleen whales that were geometrically similar to one another (all body lengths being proportional to body size). Although rorqual allometry enhances engulfment capacity for a single lunge, the cost associated with it could limit access to food in the deep ocean. From this line of reasoning, we have speculated that the allometric scaling of lunge-feeding energetics has imposed an upper limit on body size in rorquals. It is interesting to think about why an animal isn’t, or wasn’t, larger than a blue whale, and clearly more studies are needed to explore this hypothesis and others related to limits on big body size. Evolution may have driven the size of these largest of marine mammals to their current scale, but physiological constraints related to filter feeding may also have imposed an upper bound past which they can grow no farther.
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.