The Biology of What Is Not There
By Robert Dorit
Is it only natural selection that guides the shapes seen in nature?
Is it only natural selection that guides the shapes seen in nature?

DOI: 10.1511/2011.88.20
Understanding the living world seems challenge enough for biologists. Technological advances have produced a cascade of data—from detailed genome sequences to the sophisticated satellite imagery that documents the planet’s ecosystems—but our ability to make sense of these data still lags far behind their acquisition. With such a backlog, the idea that we might want to think about objects that are not real seems, frankly, capricious.
Yet without thinking about life-forms that never were, we cannot fully understand the life forms that do exist. Questions about absence lie at the very core of evolutionary biology: Is the living world we behold the only possible outcome of the evolutionary forces that produced it? Or can we imagine, instead, different unfoldings, of which this is but one? The one actual unfurling of the tree of life, of course, places restrictions on our capacity to address this question. I would argue that there are nonetheless ways of posing such queries that may prove productive.
The most accessible example of how to examine the shapes of the possible comes from work on shell forms carried out in the 1960s by American paleontologist David Raup and his collaborators (see the first figure). Shell shapes are beautiful; they are also geometrically well behaved and can be described relatively easily in mathematical terms. The mathematical model of shell shape, at its most basic, includes the rate at which a shell grows around its central axis, the rate at which it descends down that same axis and the rate at which the shell opening expands as its architect grows. With these three parameters we can depict a three-dimensional shape space: Any point in that space defines a single shell shape that may or may not occur in the living world. Real shell-bearing organisms are varied, abundant both in the current biosphere and in the fossil record, and their shapes can be plotted onto the shape space we have defined. When we do so, the pattern is striking. Certain regions of the cube, shown in color, are densely occupied, but most of the cube is uninhabited.
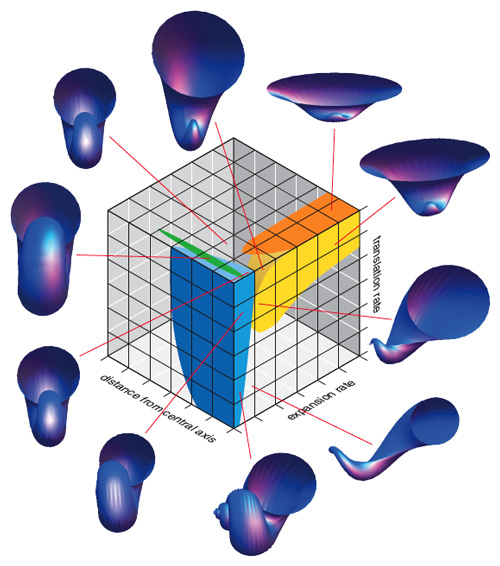
Illustration by Barbara Aulicino and Robert L. Dorit. Adapted from D. M. Raup, 1966, Journal of Paleontology 40:1178; shell shapes drawn in Mathematica.
The challenge of understanding the distribution of biological objects in shape space thus consists of two separate, but interrelated, problems. The first of these problems involves the definition of the space of possibilities. For snail shells, we are fortunate, because the shape is mathematically tractable (a logarithmic spiral is a reasonable first approximation). The shape also involves a limited number of variables (in this case, three, which allows us to depict the space as a three-dimensional cube). For other biological shapes at other scales, defining the shape space may be considerably more challenging. How, for instance, do we define the space of all possible protein or RNA shapes? What mathematical expression will capture all of the possible architectures of tree shape? Not only are these spaces likely to be of a higher dimensionality, making them harder to depict, but the underlying mathematical function that can generate the shapes is likely to be far more complex.
The second problem with understanding shape distributions involves mapping the real objects of the world onto the shape space that we have constructed—and then accounting for the distribution of these realized forms. And it is here that we find an astonishingly consistent result. In every case studied, the distribution of realized shapes is nonisotropic: Some parts of the cube are densely populated with realized shapes, whereas others are virtually, if not entirely, empty. Such patterns in biology demand an explanation. What is this strange occupancy of shape space at all scales telling us about the forces that give form to the living world?
The temptation to attribute the occupancy of shape space to the action of natural selection is almost irresistible. In this optimalist light, the occupancy problem is easily dismissed: What is there is what works; what is not, doesn’t. Yet this easy solution may be based on a set of problematic assumptions. To be sure, the objects of the real world—shell shapes in our example—do function effectively in their environment, or natural selection would have made short work of them. The nautilus shell is a stunning example of how propulsion and buoyancy can be elegantly balanced, and biologists and naval engineers alike justly admire its shape. The barnacle shell has indeed evolved a shape that enables its tenant to survive the pounding of the waves, and the rising and falling of the tides. But the fact that natural selection acts incessantly to shape the natural world does not mean that anything that we do not see has been tested by natural selection and found wanting. What that formulation assumes is that every corner of shape space is accessible, that every conceivable shape in our cube has in fact been tried—which is to assume too much.
Evolutionary theory, especially in its Anglo-American formulation, has traditionally favored the idea of natural selection as the driving force that shapes living form. Natural selection is indeed a powerful chisel, but a complete theory of evolution also needs to take into account the material being chiseled. The occupancy riddle will not be solved until we think about how organisms are actually built, and until we give history its proper due as an architect of form.
Constructionist explanations for the occupancy of shape space acknowledge that not all corners of shape space are equally accessible. Under this rubric, the occupancy of shape space derives (at least in part) from the consequences of how biological forms are constructed. Organisms have ontogenies, and the way they develop from a fertilized single cell into a final adult form has implications for the resulting shape. Thus, to stay with our shell-shape example, it is unlikely, if not impossible, for the opening of the shell (where new material is deposited) to decrease in size as the animal matures. Organisms tend to get bigger as they mature. Even though it is possible to model a logarithmic spiral whose leading edge grows and then shrinks, that excursion in shape space appears to be inaccessible to real organisms. Importantly, this inaccessibility is not due to the fact that such a shape would not function and thus would be eliminated by natural selection. Instead, we do not see it as a realized shape because, given the rules that govern shell construction, it occupies forbidden territory. Given how shapes are made, certain among them cannot even show up to participate in the struggle for existence.
Proteins too have ontogenies, dictated by folding rules. And similar forbidden zones in shape space exist at the molecular level. Knots, for example, are notoriously scarce in proteins, for reasons that flow both from the chemical character of the amino-acid components of proteins and from the mechanisms that govern protein folding. (In the interest of full disclosure, I should note that until fairly recently we thought knots to be a virtually impossible geometry for real proteins to adopt. We were wrong. They are rare, but not impossible.)
In our search to account for the occupancy of shape space, we have much to gain by paying closer attention to the rules and mechanisms that generate form. Simultaneous progress in computational methods and developmental biology repeatedly leads to the same conclusion: Simple rules can give rise to enormously complex forms. A graphic example, first described by British physicist and mathematician Stephen Wolfram, is shown in the second figure. In this computer simulation, a simple set of generating rules (such as “branch out into 3 [or 2 or 4], increase the branching angle by 15 degrees, repeat”) gives rise to an array of leaflike forms. These forms are striking in their variety. Note, too, that every shape is discrete and does not appear to blend with an adjacent shape: The generating rules themselves populate shape space in characteristic ways, overstuffing certain parts of it while leaving others nearly deserted. By attending to the construction of biological forms, we can begin to appreciate just how much pattern and structure can arise before natural selection even has a hand in the process.

Image adapted from Stephen Wolfram, A New Kind of Science, 2002, Wolfram Media Inc., p. 402. http://www.wolfram.com
Provocative as they are, however, these relatively simple simulations need to be interpreted with caution: They are not meant to simulate the actual biological mechanisms of leaf development. We have yet to elucidate fully the actual dynamics that determine leaf shape. Similarly, we need to remember that the developmental process—the biological counterpart of the computer program that created these leaf shapes—itself evolves. Indeed, the evolution of developmental programs has resulted in the opening up of regions of shape space that might previously have been inaccessible. For instance, take the Cambrian explosion some 600 million years ago. Changes in the rules of construction, coupled with changes in the geochemistry of the oceans, suddenly allowed certain groups of marine organisms to make hard shells. Whole new dimensions of shape space abruptly opened, and the diversity of organisms on this planet was forever changed.
Although the constructionist perspective enhances our ability to account for the distribution of biological objects in shape space, it lacks an acknowledgment of the role that history plays in the filling of shape space. At its most basic, history matters because evolution often works by composing variants on a theme. As a result, once a functional shape evolves, the adjacent shape space is most likely the first to be fully explored. This tendency to remain in the shape neighborhood of one’s ancestors is further enforced if the existing shape is surrounded by less-functional alternatives. Evolution will not cross through less-fit alternatives even if better-functioning alternatives lie within view.
The extent to which history controls the distribution of realized shapes also depends on just how easily one shape can be transformed to the next. In our shell example, we can safely claim that cone shells, in terms of transformation, are conservative. They give rise to other cone shells, both from one generation to the next and over evolutionary time. The corner of the tree of life represented by the genus Conus is bushy indeed, with over 3,000 named species, each of them crowded into a distinctive zone in shell space. But for shapes at other scales—the shape of folded RNAs, for instance, or the shape of proteins—a few changes in the sequence may suffice to cause a flip from one location in shape space to a completely new location.
Perhaps if every lineage had world enough and time, if the tree of life had an infinity to explore shape space, it would eventually discover every successful form that could be built given constructionist constraints. But history dictates that because the evolutionary life of most lineages is brief, many paths and shapes remain unexplored.
Having defined the universe of the possible, we will have to populate it with the actual. We will need statistical approaches to determine whether there are over- and under-populated zones beyond what we would expect from sampling alone. We will need to flesh out the consequences of the ways in which living form is built and the constraints imposed by the materials of life. We will need to elucidate the role of time and history in shaping shape. And only then will we be able to invoke the sculpting power of natural selection. Yet daunting as the occupancy problem is, the nonisotropic distribution of realized forms appears both universal and independent of scale. Such regularity in biology is strangely beguiling.
When you next look out at the stars, notice how some parts of the night sky are teeming with stars, whereas others seem comparatively dark. This is no optical illusion. At all scales, and for all of the classes of objects that astronomers can identify—stars, galaxies and constellations—the universe, too, is nonisotropic. The variability of the heavens, like the variety of living things, underlies much of their beauty.
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.