Tying Water into Knots
By Fenella Saunders
A single ring is easy—how about a chain or a trefoil?
A single ring is easy—how about a chain or a trefoil?

DOI: 10.1511/2013.102.192
William Irvine was a little discouraged. The University of Chicago physicist had a bit of a hobby in trying to make special vortex rings. A vortex is a spinning current, such as a tornado. A vortex ring is like a tornado flipped on its side with its ends joined—a common example is a smoke ring. For about a century, researchers have been trying to make vortex rings that linked together, without success. Irvine had taken up the challenge. He had attempted the traditional approach of colliding rings together, but they pulled apart. “Because the idea has been there for so long and nobody seemed to have done it, you worry that it’s not doable at all,” he says. But then he took inspiration from dolphins, which regularly blow perfect bubble rings. “They don’t do linked ones, but the rings that they make have a certain robustness to them,” Irvine says. So he kept at it. He and his postdoctoral student Dustin Kleckner figured out that shaped holes produced shaped rings well. So why not create a hole whose edge looks like a knot?
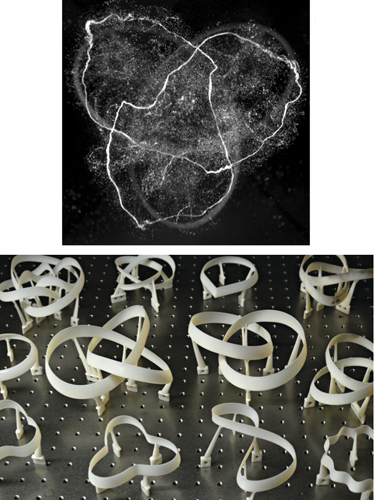
Images courtesy of Dustin Kleckner and William T. M. Irvine.
Irvine and Kleckner used a 3D printer to make a series of hydrofoils—structures contoured like an airplane wing, with a rounded front and a tapered back edge, but used in the water—that looked like linked rings or trefoil knots (see image above, bottom). They placed the hydrofoils in water that was entrained with microscopic bubbles, allowing the bubbles to coat the hydrofoil surface. Then they quickly accelerated the hydrofoils, leaving behind a vortex ring in the shape of the structure, which the bubbles traced (see image above, top). They were able to image the ring using a high-speed camera and a laser beam spread out into a sheet, which illuminated the bubbles in slices. The light slices were then stacked up by a computer, in a method similar to a type of medical imaging called computed tomography.
Irvine compares the vortex generating process to an airplane on takeoff. “A wing always creates a flow around itself that is faster over the top than the bottom and circulates around. If you have short wings, the vortex tries to continue coming off the edges and creates a tip vortex. But when you accelerate from a stand-still, it can’t create circulation from nothing, so it has to be balanced by an opposing vortex that is left behind.” That remaining vortex is the one Irvine and Kleckner can image.
Single vortex rings are very stable, but the knotted rings start to stretch out. This activity would seem to defy rules about the conservation of energy, so the rings have to basically change shape to get around this point. They reconnect with themselves and come out as two separate loops. (See movies here.)
There are a number of physical processes where knots may come into play: plasma loops in the Sun’s corona, reconnections in the Earth’s magnetosphere, cosmic strings, superfluids (which have zero viscosity) of ultracold liquids and gases. Although Irvine’s bubble-coated knots are not replicas of these phenomena, new properties could be discovered by bringing these largely unobservable processes down to a laboratory scale. “The physics is analogous not in a trivial way, but also not in a precise way,” Irvine says. “There are a lot of processes where the basic rules of the game involve things like vortices and flow, and they can do all the things that you see in this experiment. They can knot and also reconnect.”
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.