American Scientist

The Earth is not at the center of the universe, a conclusion we owe to the model of the universe created by 15th-century mathematician and astronomer Nicolaus Copernicus. The inference that we are therefore cosmically ordinary is sometimes called the principle of Copernican mediocrity. As 20th-century astronomer Carl Sagan put it, “We live on an insignificant planet, of a humdrum star, lost in a galaxy, tucked away in some forgotten corner of a universe.”

Modern science has, like Copernicus, revolutionized the way we conceive of the universe, and its findings are typically used to reaffirm Copernican mediocrity. Successes from cosmology to genomics have even infused many scientists with enough hubris to boast of our insignificance. “We are so insignificant that I can’t believe the whole universe exists for our benefit,” says physicist Stephen Hawking. His belief is not uncommon and often derives from a worldview that presupposes such insignificance, with the further implication, ostensibly implied by Darwin’s theory of natural selection, that humanity is the meaningless product of evolutionary processes.

It behooves us to beware of presuppositions, especially as 21st-century science, from physics to biology, expands the ways we understand the world. The assumption of mediocrity can be just as misleading as the earlier belief of superiority. Even the historical paradigm of Copernicus toppling the Earth from its pedestal is deceptive. Historian Dennis R. Danielson emphasizes that Copernicus and his contemporaries did not actually think that the Sun-centric system pushed humanity into insignificance. On the contrary, the prevailing Greek and Christian views held that the Earth was located, as the 15th-century Italian philosopher Giovanni Pico put it, “in the excrementary and filthy parts of the lower world,” where gross, imperfect, mortal beings reside. By putting the Sun at the center, Copernicus effectively elevated humanity to a place closer to the heavens. In the post- Newtonian world, however, the center came to be seen as the place of primacy, and a Sun-centric system appeared to demote Earth to mediocrity.

In particular, two dramatic recent developments in modern astronomy—the discovery of planets around other stars and the formulation of inflationary Big Bang cosmology—suggest we may not be so ordinary after all. It could be time to reexamine the notion of our mediocrity and, if we might be special in some way, consider the ethical challenges surrounding the welfare of our planet.

A Fertile Planet in a Hostile Universe

It took intelligent life roughly 4 billion years to develop on Earth. We don’t know the range of nurturing conditions that allowed intelligence to thrive, but we do know that our planet is unique within the Solar System. Its salubrious environment should not be taken for granted. The cosmos is vast, however, and hosts a diverse array of worlds whose properties and capacity to host life we have now begun to study. If we really are ordinary beings, then at a minimum intelligent life should be commonly found on other worlds. But, as the physicist Enrico Fermi famously noted, if aliens are common in the universe, where are they?

By putting the Sun at the center, Copernicus elevated humanity closer to the heavens. In the post-Newtonian world, however, the center came to be seen as the place of primacy, and a Sun-centric system demoted Earth to mediocrity.”

• Facebook
• Twitter

Only life capable of conscious, independent thought and an ability to communicate between stars is under consideration; if only alien bacteria exist, then we are certainly not a mediocre species. The discovery of primitive life forms elsewhere in the universe would help us reconstruct how intelligence on Earth evolved, but unless a species can communicate with us, we will still be unique and alone, with no one to teach or learn from, no one to help us solve our problems, or—in the fanciful extrapolations of filmmakers—no one to battle with. To guess the number of possible extraterrestrial civilizations, scientists try to identify all the varied steps needed for life to arise, evolve, and mature to intelligence, and then assign a probability to each step. This calculation is known as the Drake equation, named after American astronomer Frank Drake. It is a set of multiplicative factors used to track the various phenomena thought to be necessary to yield intelligent life (see the figure below, and the author’s article in the July–August 2011 issue).

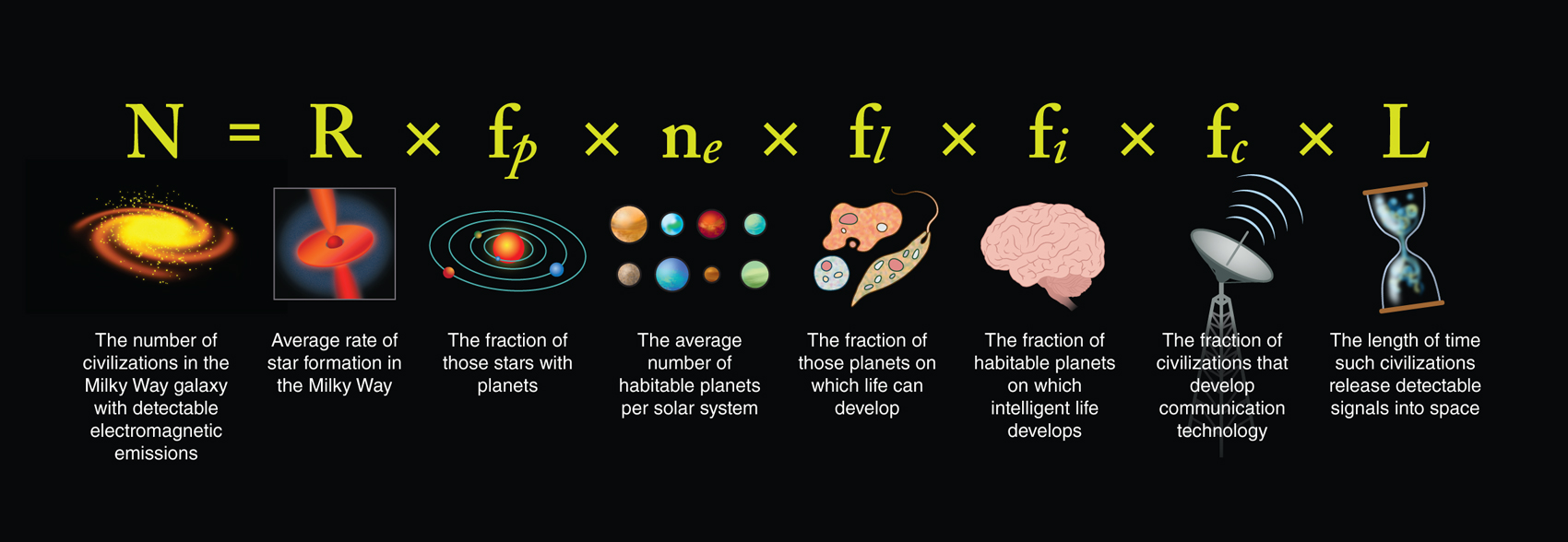
Breakthroughs in exoplanet detection address one key term in the Drake equation, the frequency of planets capable of nurturing extraterrestrial intelligence (ETI). Natural philosophers since the ancient Greeks have expected planets, and life on them, to be commonplace. Percival Lowell, an astronomer famous for his claim that there were artificial canals on Mars, wrote in his 1908 book Mars as the Abode of Life, “From all we have learned of its constitution on the one hand or of its distribution on the other we know life to be as inevitable a phase of planetary evolution as is quartz or feldspar or nitrogenous soil. Each and all of them are only manifestations of chemical affinity.” Today, every schoolchild knows that Mars has no artificial canals, and no aliens either. Lowell’s rhetorical confidence was based on presuppositions about life that no one would make today. Other optimistic assumptions have been made, however. Just a few decades ago textbooks taught that practically all moderate-mass stars hosted exoplanetary systems like our Solar System with an Earth-like planet capable of bearing intelligent species. As astronomers Donald Goldsmith and Tobias Owen put it in their 1993 textbook, The Search for Life in the Universe, “Nothing in our theories for the origin and evolution of our Sun is unique to the Solar System... The chances seem good that one of these inner planets will orbit its star at the right distance [to host life]...We say one in every two to be conservative.”

So far, more than 3,600 confirmed exoplanets have been detected. The NASA Kepler mission alone, launched in 2009, has identified more than 2,300 of them. Many of these exoplanets have had their mass, radius, and other properties measured. NASA’s Transiting Exoplanet Survey Satellite (TESS), scheduled to launch in 2017, will find many more. The exciting discovery is not that exoplanets exist; it is that they are so varied.

To guess the number of possible extraterrestrial civilizations, scientists try to identify all the varied steps needed for life to arise, evolve, and mature to intelligence, and then assign a probability to each step.

• Facebook
• Twitter

In assessing whether a planet can nurture life, the usual starting assumption is that it needs liquid water and therefore should orbit its star in the habitable zone, the so-called Goldilocks distance (not too hot, not too cold) at which the planet’s surface temperature allows water to be liquid. This distance can be estimated from the planet’s orbital parameters and its star’s temperature. So far, dozens of exoplanets have been found in their habitable zones. Astronomers extrapolating from the statistics of exoplanets discovered to date have concluded that, at least for some classes of stars, there is likely to be an exoplanet in its habitable zone.

Five dramatic, recently discovered exoplanets—called Proxima Centauri b, TRAPPIST-1e, TRAPPIST-1f, TRAPPIST-1g, and LHS 1140b—are orbiting dwarf stars (a class of stars fainter than the Sun) whose surface temperatures could permit liquid water to exist. There are, however, significant limitations for life on these planets. Planets orbiting small stars have habitable zones that lie very close to their stars because of the cool temperatures of those stars. Even though it is in the habitable zone, a planet in this close region tends to have one side perpetually facing the star—a situation that is called gravitationally locked— leaving half the planet in the dark and half constantly illuminated. This class of cool, small stars, known as M-dwarfs, have an interior circulation that is almost entirely convective, transporting upward hot gas from the deep interior; in contrast, the Sun only has convection in its surface layers. This type of circulation in M-dwarfs leads to coronal flares, x-ray emission, and strong stellar winds, all of which might be hazardous to life on a nearby planet in the habitable zone. For example, the planet orbiting the cool star Proxima Centauri, the closest star to the Sun, has an orbital period of 11.2 days and is close enough to be in the habitable zone, making it a prime target in the search for life. But the star’s active flares, winds, and x-ray radiation may well have stripped away any ocean or atmosphere on the planet.

The habitable zone requirement is only one of many conditions necessary for an exoplanet to host intelligent life. In Rare Earth: Why Complex Life Is Uncommon in the Universe, paleontologist Peter D. Ward and astronomer Donald Brownlee show why even simple life forms need much more than just liquid water to exist. The right ingredients are also needed, yet the chemical elements are not uniformly abundant throughout the universe. Also essential is an environment that remains stable for billions of years. Other factors—such as orbital eccentricity, which is calculated by comparing the farthest distance of the planet’s orbit from the center of the star with the closest distance of the orbit from that center—also affect suitability for life. Eccentricity determines the annual variations the planet receives in stellar illumination, as well as its susceptibility to gravitational orbital perturbations and disruption by other planets whose orbits might cross nearby. With an eccentricity of approximately 0.017, the Earth’s elliptical orbit is nearly circular. Only 5.3 percent of exoplanets currently listed by the Extrasolar Planets Encyclopaedia, an online database developed by an international consortium of astrophysics institutions, have an orbital eccentricity less than or equal to that of Earth.

The results reinforce that an enormous variety of systems exist, consisting of a diverse range of often bizarre environments that is considerably broader than was imagined before the first ones were discovered. As the MIT exoplanet scientist Sara Seager put it in her 2010 book, “It seems that less than 10 to 20 percent of Sun-like stars could host Solar System copies. Instead, astronomers have found that exoplanets and exoplanetary systems are incredibly varied, with planets of nearly all conceivable masses and sizes as well as orbital separations from their host star.” Scientists and journalists regularly describe new exoplanets as being potentially habitable, but in this early stage of the enterprise, such descriptions often mean that the planet is located within a star’s habitable zone and probably has a rocky composition. In the next decade, with the advent of NASA’s James Webb Space Telescope and large ground-based telescopes, astronomers expect to be able to better study the atmospheres potentially surrounding some of these candidates, whose chemistry could reveal potential for life.

So far the focus has been on the exoplanet term in the Drake equation estimates for extraterrestrial intelligence. However, the equation’s most uncertain terms are not astronomical but its three biological ones: the probability that life develops on a suitable planet, that it evolves to be intelligent, and that it survives a long time. The formation of life, even in a perfect laboratory setting, and its evolution are the subjects of a vast and sophisticated literature; there is plenty of speculation about whether a civilization can survive for a long time as well. Perhaps here it is enough to note that geneticists have concluded that the evolution of DNA on Earth was circuitous and probably included many fortuitous accidents. Evolutionary biologist Stephen Jay Gould argued that evolution itself, at least on Earth, followed a very unlikely path, with large brains by no means a guaranteed outcome. Although the same physical processes operate everywhere, some sequences of events— including biological ones—could be astronomically less likely to happen than others. The evolution of intelligence could certainly be such a sequence.

Communicating with Aliens

It does not matter whether aliens thrive in the distant reaches of space. What matters is whether we know of their existence. Because most of our galaxy, not to mention other galaxies, is too far away for us to be able to image alien artifacts directly or to obtain other direct evidence of intelligent activity, the best method would be to look for radio signals. Until such signals are detected, we are just guessing about the existence of aliens. To focus the discussion and facilitate quantitative analyses, consider only the volume of space that we can probe in 100 generations, a time frame that is practically forever in a subjective sense. This is, of course, an arbitrary timescale. If we consider a smaller volume—say, one that’s accessible within only a single generation—the chances of our finding aliens go down by a factor of a million, because the number of stars is proportional to the volume of space and scales with time (or distance) cubed—but we will have a yes-or-no answer 100 times sooner. One generation is about 25 years, and because at least one round trip of messaging is necessary, 100 generations of time corresponds to a distance of about 1,250 light-years from Earth. In this region of space there are about 30 million stars of all types. If the chances for extraterrestrial intelligence developing around a planet were just 1 in 30 million, we would probably be alone in this cosmic neighborhood. The Search for Extraterrestrial Intelligence (SETI) program that Frank Drake helped establish takes the position of its Bernard M. Oliver Chair for SETI Research, Jill Tarter, who asserted in Science in 1983 that “the only significant test of the existence of extraterrestrial intelligence is an experimental one.” But the enormous limitation imposed by the finite speed of light means that even if there were a network of advanced civilizations living on the other side of our galaxy, they would be much too far away from Earth to communicate with us on human timescales. Furthermore, any signals not pointed towards us would probably not be detected.

When SETI started more than 50 years ago, it used relatively primitive technology and probably could not have spotted an Earth twin if it were 1,250 light-years away. Today, the program boasts much better search technology. According to the SETI “Breakthrough Listen” website, the institute could detect a civilization around any of the 1,000 nearest stars if it transmitted towards us even with only the power of common aircraft radar. So far, we haven’t detected anything, but in much sooner than 100 generations we will probably be able to reach some statistically significant conclusions about results—including null results.

Even if the Milky Way galaxy has millions of water-bearing Earth-size planets, and even if the formation of life were inevitable on every planet in the universe with liquid water, the previous arguments suggest that we and our descendants for at least 100 generations are probably living in solitude. Of course we can expand the volume of our search to improve the chances of finding extraterrestrial intelligence, but then we will have to wait even longer than 100 generations to find out. The Misanthropic Principle expresses the idea that the many possible environments in our cosmos are so varied and uncooperative, or hostile, either always or at times during the long gestation and maturation times apparently needed for intelligence, that it is unlikely for intelligent life to evolve and thrive. Life on Earth may not be ordinary. We may be isolated and truly alone.

Cosmic Fine Tuning

In thinking about mediocrity, with its connotation of being not just statistically average but also insignificant, there is a second principle to consider: The physical constants of the cosmos seem to be remarkably finely tuned to facilitate hosting intelligent life. Although any kind of intelligent life is implied, not just human life, this observation is almost always referred to as the Anthropic Principle.

We live on a planet with liquid water orbiting in the Sun’s habitable zone, one that possesses many other hospitable features, from a favorable chemical composition to tectonic plates. No other place in our Solar System is even close to being like it. But the universe is a big place, and our galaxy alone has nearly a trillion stars. It is possible that a paradise like Earth will randomly develop somewhere in the universe. In this way of thinking, we are not lucky. We are just in the place where we can be.

The habitable zone requirement is only the first of many conditions necessary for an exoplanet to host intelligent life. The proper abundance of heavy elements and an environment that remains stable for billions of years are also necessary.

• Facebook
• Twitter

If, however, the fundamental constants of the universe took values much different from the ones they have— constants such as the speed of light or the strengths of the four physical forces (gravitational, electromagnetic, strong, and weak)—we would not be here. The most extreme example of fine-tuning is the expanding universe in the inflationary Big Bang description of creation. Physicists estimate that if the balance between cosmic effects were different by only one part in 10¹²⁰, we would not exist (although there is disagreement about exactly how fine-tuned the constants really are; Fred Adams of the University of Michigan, for example, has recently calculated some much less restrictive scenarios). The Anthropic Principle has been contemplated for decades since theoretical physicist Paul Dirac first called attention to the curious balance between large cosmic numbers. A universe fined-tuned to nurture intelligent life is the second piece of evidence for the end of our Copernican mediocrity.

Why is the universe so suitable for intelligent life? It could just be dumb luck. Or, as commonly proffered by theoretically minded scientists, there are an infinite number of universes, also called a multiverse, spanning all logical possibilities. We live in the universe we can, in an argument similar to the preceding one about the Earth just being the one planet out of many where we can exist. The third answer touches on philosophy and quantum mechanics and is much more uncertain, controversial, and provocative. The traditional interpretation of quantum mechanics describes matter as being composed of wave functions of probability that only become real entities when measured by an observer. The quantum mechanical pioneer John Wheeler even championed the notion that the universe had to evolve conscious beings in order to become real. This notion—sometimes called the Participatory Anthropic Principle—is still included in modern texts.

It seems to be a cop out to argue that we are lucky, and as a physicist trained to give preference to simple solutions, I find the multiverse explanation to be too exorbitant a solution. The quantum mechanical explanation is uncomfortably mysterious, but quantum mechanics has other mysteries too, so of the three solutions, it has the most potential. Still, the basic point is troubling, especially if one believes in a reductionist worldview that presupposes our insignificance—troubling because it suggests that something steers the universe toward intelligence, and humans are representatives of that teleological endpoint. If we might be the only such intelligent beings around (or the only ones that we will know about for millennia or longer), then we are more than just mediocre, we are special. Our 21st-century perspective is very different from the 16th-century one of Copernicus and his colleagues. We know about and can appreciate the immensity of space and time, the complexities of genetics and evolution, and the power of statistics. Even though the Earth is not at the center of the universe, its luxuriant environment could nonetheless make it a rare oasis. Perhaps we can appreciate that humanity, too, could be unusual, even special and not mediocre, at least as far as we are likely to know for a very long time.

The End of Copernican Mediocrity

The Misanthropic Principle raises epistemological and ethical dilemmas. The epistemological quandary is simple: Not knowing about the existence of extraterrestrial intelligence does not mean it does not exist somewhere out there. But until we hear a clear signal from beyond, or until science provides some conclusive argument, we are ignorant about putative aliens.

The second dilemma is ethical: The Earth is under stress, and humanity confronts misery. It has taken 13.8 billion years of cosmic history to develop the rich biosphere that we enjoy and sometimes take for granted. If our world is just an evolved collection of atoms, then perhaps its future health and welfare are not a great concern; in a cosmos abundant in life, it is possible some alien civilizations will survive even if the Earth’s does not. But if the human race—as far as we are likely to know for millennia—is singular, then we must consider the possibility that neither our planet nor ourselves are products of common happenstance. This thought adds urgency to the cause of protecting our rare planet and its precious inhabitants.

Once the ideas of Copernicus took root, and people realized that the cosmos was not geocentric, they began to think about their world, humanity, and themselves in a new light. Building on the rapid advances of science after Newton, they concluded that because the Earth seemed to be ordinary, humanity too was ordinary—mediocre. Modern scientific evidence questioning Copernican mediocrity should initiate a similar process of self-reappraisal. We seem to be unusual—although it’s unlikely we’ll know how unusual for a very long time. It is possible that we are just an accident, but conscious life does appear to be a remarkable and unanticipated achievement of the universe, with attributes that are not predicted for an ensemble of atoms. The Anthropic Principle, at least in some interpretations, intimates that some necessary feature of nature endowed the cosmos with this capacity, making it fundamental to the Big Bang and steering it over eons of evolution to produce conscious beings. We are representatives of that teleological end point.

Writing about the impact of the discovery of exoplanets, in 2010 Seager and astronomer Jack J. Lissauer made the claim that “we will at last complete the Copernican Revolution…. We are on the verge of, if not in the very midst of, the greatest change in perspective of our place in the universe since the time of Copernicus.” Perhaps their claim will prove true. But if honestly considered, that change of perspective is much more likely to be in the direction opposite to the one that these authors imagine: toward reclaiming our exceptional status.

The case for the end of mediocrity necessarily rests on incomplete data, statistics, and an admission that there are many things that we still do not understand.

• Facebook
• Twitter

The case for the end of mediocrity necessarily rests on incomplete data, statistics, and an admission that there are many things that we still do not understand. We might have to wait in ignorance for millennia before we have more complete stellar surveys indicating whether other civilizations are likely to exist. Even so, as we wait for more information about aliens or quantum physics, we should be able to acknowledge that the story is subtle and that there is compelling evidence that humanity is precious. The Earth, even if it is not unique, is for all intents and purposes a special place. The implication of the Anthropic Principle is that it might matter. The implication of the Misanthropic Principle is that we have to care for our planet and one another by ourselves—without help from alien insights or technologies. Modern science has prompted this reevaluation, but addressing it will require the best of all our human abilities.