Multiscale Modeling in Biology
By Santiago Schnell, Ramon Grima, Philip Maini
New insights into cancer illustrate how mathematical tools are enhancing the understanding of life from the smallest scale to the grandest
New insights into cancer illustrate how mathematical tools are enhancing the understanding of life from the smallest scale to the grandest

DOI: 10.1511/2007.64.134
The 1966 science-fiction film Fantastic Voyage captured the public imagination with a clever idea: What fantastic things might we see and do if we could miniaturize ourselves and travel through the bloodstream as corpuscles do? (This being Hollywood, the answer was that we'd save a fellow scientist from evildoers.)

20th Century Fox/The Kobal Collection
A generation later, many wonder why we'd go to the trouble of shrinking ourselves. Now we can easily "see" into blood vessels, into cells themselves, with nanosize detectors, DNA assays, digital imaging tools and advanced microscopes. We have only to turn on the television to take a digitally simulated voyage deep into the body of a crime victim. And scientists have the tools to examine life at almost any scale imaginable—to scan the solar system for biomolecules, monitor changes in global vegetation from satellites, watch blood flow inside the brain or locate a point mutation in a chromosome.
But that's the problem with biology. Life has so many scales, each rich and complex, that progress has required the field to be sliced up. Some scientists are molecular biologists, others cellular, organismic or population biologists; still others study broad issues emerging from the perspectives of evolution, ecology or bioinformatics. Biology at each level incorporates information from strata above and below. With tools and resources ample enough to parse whole genomes, our view of life is no longer limited by our instruments.
But information can easily outrace the theory needed to understand it. As each layer of life becomes more transparent, what is revealed is more complexity than could have been imagined. Consider the brain, astoundingly complex from its convoluted outer folds right down to the intricate chemistry and nanosecond networking capabilities of its neurons. Ponder malaria, a disease involving the complex life cycles, behavior and genetics of host, pathogen and vector, not to mention climate and evolutionary factors, predators, coinfection and the like. Or, finally, cancer, a destructive disorder arising over time and space from the complex genetics and environmental interactions of animal cells.
Firmly rooted in observation and experiment, biology for decades had little use for mathematical modeling, which was, in any event, a slow business until computers made it possible to simulate large complex systems of nonlinear equations. Today biologists and mathematicians desperately need each other—not just to find structure in the vast quantities of data flowing from experiment but also to integrate this information into models that explain at multiple scales of time and space how life works. Trees branch, fish grow scales, bacterial colonies form dendritic patterns, birds flock, tumors invade organs, grasses colonize a bare riverbank. Much of life is emergent, a complex system growing out of the interaction of simple elements. New tools are helping us see the regulatory and adaptive properties that characterize all biological phenomena. With the computing power to harness some of the data now available, and with insights offered from old and new mathematics, modelers are making progress on many fronts.
Mathematical models of biology today rest firmly on time-tested and classical ideas. Imagine, for example, a bacterial colony in which each cell divides every hour. Until it begins to hit resource limitations, the population doubles every hour, a process that leads to exponential growth of the colony. Such a process is mathematically described by the exponential function, first introduced by the 18th-century mathematician Leonhard Euler, whose tercentenary will be celebrated on April 15.
Euler, well known for his major contributions to physics and engineering, could not have known that his function would describe the growth and decay of any population, or that it would someday be used to study the degradation of proteins and other biomolecules. But Euler's contribution to biology is even broader: Oscillatory processes such as circadian rhythms, which are generally described in terms of sinusoidal functions, can be very conveniently manipulated using exponential functions. Euler made significant theoretical contributions to other core concepts in mathematical biology, including partial differential equations and the topology of networks.
Four centuries before Euler was born, the mathematician Leonardo of Pisa had been modeling a hypothetical population of fast-breeding rabbits when he discovered his remarkable sequence, the Fibonacci numbers. And of course Euler has had many famous scientific descendants. Thomas Malthus relied on an exponential-growth model to make his famous prediction about human population growth. Soon Malthus's intuition yielded to a somewhat more sophisticated model of populations, which predicted that populations of predators and prey in a resource-limited environment would oscillate. This model, using the equations of biologist Vito Volterra and chemist Alfred Lotka, has played a central role in our growing understanding of ecological dynamics.
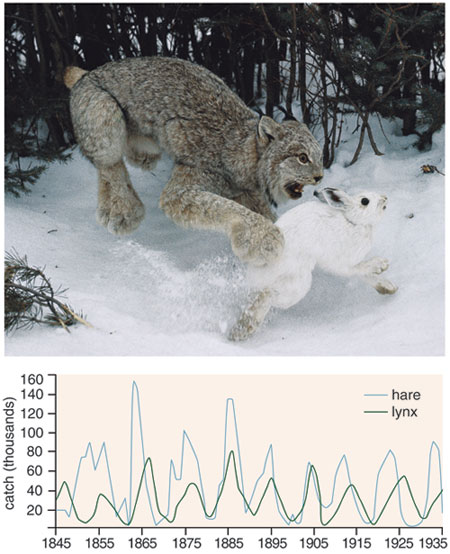
Photograph by Ed Cesar/Photo Researchers, Inc. Graph adapted from Eugene Odum's Fundamentals of Ecology, 1953, by Stephanie Freese.
The Lotka-Volterra equations, developed in the 1920s, stand as a famous example of theoretical collusion between the sciences. Equations that Lotka had used to describe a theoretical chemical reaction that oscillated indefinitely turned out to model fluctuations in fish populations in the Adriatic Sea, the predator and prey populations substituting for concentrations of two chemicals. When Lotka-Volterra equations are applied in two dimensions to populations distributed across a landscape, patchy spatial patterns appear. Today's computer-equipped ecology students routinely plug field data into lattice-style simulations and watch complex dynamics emerge.
Chemistry was also the source of another essential modeling concept in biology, that of the reaction-diffusion system. The first of this broad class of naturally occurring processes was identified in 1906 by chemist Robert Luther, who found that autocatalytic chemical reactions may exhibit wavelike phenomena in the presence of diffusion. The reaction in these systems is provided by autocatalysis. Shortly after this discovery, R. A. Fisher—one of a growing number of modelers working in genetics, epidemiology and population analysis as the 20th century progressed—realized that the spread of an advantageous gene in a population could be modeled by a reaction-diffusion equation.
Photograph by Eye of Science/Photo Researchers, Inc. Illustrations by Barbara Aulicino.
The concept of pattern formation arose in mathematical biology during the same fertile period, as the naturalist D'Arcy Thompson tackled the challenge of how to account for the shape and form of organisms. Thompson discovered that new patterns in morphogenesis (the generation of form—say, the shape of a mollusk shell or the limbs and tail of a cat) could be understood as self-organizing systems.
The connections Thompson drew between biological and other phenomena inspired continued theoretical work, and in 1952 the modeling of pattern formation took an unexpected leap. Alan Turing (better known today as the father of computer science) showed using a simple mathematical model that a system of chemicals, stable in the absence of diffusion, could be driven unstable by diffusion. The result was highly counterintuitive, since diffusion generally leads to a stable equilibrium. Turing suggested that the chemical pattern set up by the instability could serve as a pre-pattern for a cellular response. If one of the chemicals is a growth hormone—he labeled this a morphogen—the spatial pre-pattern set up by the reaction-diffusion process would lead to differential growth. This could possibly explain how a spherical fertilized egg begins to form an asymmetrical animal body.

Images courtesy of Rafael Barrio; from Aragon et al. 1998.
The utility of Turing's idea began to become evident when Hans Meinhardt and Alfred Gierer came up with a type of reaction-diffusion system that would undergo the Turing instability and produce a pattern. This system, described in 1972, was made up of a pair of reacting chemicals labeled activator and inhibitor. The first activated the production of the second; the inhibitor in turn would inhibit the growth of the autocatalytic activator. Pattern formation is possible if the activator in this system diffuses much more slowly than the inhibitor, and if it has a shorter half-life. This leads to an important principle in patterning: activation at short range coupled with inhibition at long range. Biologists wondered whether Turing models might explain the spots on leopards and fish, the stripes on zebras or the complex patterning on seashells.
The field of mathematical biology can finally, with the turn of this century, be said to have matured. It is a much broader field than can be discerned from these examples, chosen for their relevance to the current work we will discuss. Many mathematical biologists today are intellectual descendants of Nicolas Rashevsky, who in 1947 formed the first organized group working in mathematical biology. Rashevsky's contributions were largely forgotten during the latter half of the 20th century, when mainstream biology remained largely qualitative. But that was then. Now much of the action in the field is in silico, in the fully quantitative fields of computational and systems biology.
For those curious about animal patterning: Yes, the pigment patterns that produce the leopard's spots and the complex patterns on many seashells have been nicely modeled as activator-inhibitor systems. We can mathematically build a fine spotted cat. But more important, we can mathematically model a tumor.
Seeing life at the cellular level remained a sci-fi fantasy for a surprisingly long time. As recently as the 1980s, model-building was done on a continuum. The behavior of single cells was hard to quantify, and most mathematical biologists were mathematical physicists working in fluid dynamics. Now that we can study cells in action, we can build models at the cellular level and validate them with experimental observations. But this is hardly the only reason to focus intently on the cell.
The discovery of the cell as the microscopic unit of life changed the way life itself is understood. The bodies of living things are composed of cells, and cells in turn are made up of multiple interacting pieces and parts. The plant and animal worlds can be studied as hierarchies: atom/ion, molecule, macromolecule, organelle, cell, tissue, organ, individual, population. Information in biological systems moves both up and down these scales. This feedback is a general feature of self-organizing systems, and its analysis continues to provide novel mathematical challenges. Occupying the center, the cell provides a focal plane from which one can scale up and down. Because a cell is the minimal unit of life, it also represents the minimum level of cooperation for a functioning living unit.
Biological modeling is thus anchored in the cell as a scale factor. Subcellular processes generally happen on a much faster time scale than those above the cellular level, so that spatial and temporal scales tend to vary together. Almost as important, the myriad of microscopic interactions involving cells are the underlying cause of the order and the complex patterns we see in the macroscopic world.
Whether they are members of a community or components of a multi-cellular organism, cells interact continuously with one another and with their local environment. To talk to its neighbors, a cell mainly uses chemical signals, sensed by receptors distributed across its surface. These chemoreceptors activate or modulate biochemical pathways inside the cell to control activities such as the cell's movement.
Cells in a multicellular organism typically exist in an aqueous fluid medium. Signaling molecules exchanged through this medium diffuse and decay as they are transported along the flow patterns generated by the movement of the cells and other nearby objects.
In describing just these few facts, we have already assembled a model of biophysical phenomena whose mathematical description would require a large number of parameters. Would such a model be of practical use? Probably not. A model incorporating these facts would be highly dependent on what type of organism is being modeled; it would likely shed little light on general principles and would creak under the weight of its parameters.
Practicalities are not the only concerns. Constructing a model is something of an art. Several models might be consistent with the data at hand; they might even yield the same mathematical representation. So the first role of a model is to test verbal descriptions arising from biology. If the model produces a result that is clearly wrong, it may be that the biological hypothesis is wrong. At a minimum, modeling can refine intuition. But a rigorously developed model coupled with experiment has the potential to accomplish far more.
So where to begin? The common approach is to construct a simplified model that retains enough biology to be meaningful but has a much smaller number of parameters. An advantage of such models is that they can usually be applied to understand more than one biological system.
The signaling, motile cells mentioned above provide a classic example. Cell movement can be modeled as a group of related processes. A simple model can be constructed by defining a mathematical function that describes the relation of the input and the output—in this case, the way the velocity of a cell depends on the chemical gradient the cell senses. This function encapsulates how the cell surface senses signals, the intracellular processes by which the signals are transduced and how the machinery for movement is activated. Of course, this function cannot be determined exactly, so instead the modeler chooses a function that is known to approximately capture the underlying biology.
More realistic models of cellular movement and interaction require the use of subcellular models, which take into account chemical kinetics and the tightly packed and heterogeneous environment of the cellular cytoplasm. As one of us (Schnell) has shown, this is quite a different matter from modeling chemical activity in the homogeneous environment of a laboratory test tube. While coupling the input and output of a cell, the resulting function also couples the subcellular and supercellular regimes, and thus such a model can be used to investigate the large-scale, often visible patterns we see in nature.
Whether on one scale or many, then, modeling can serve two purposes. When the details of the biology of a system are known, a mathematical model can be used in place of the biological system, providing a way to carry out virtual experiments. In this case the model does not add to our understanding of the system; it simply replicates the system. Where the fine detail is not known, modeling serves as a tool for testing hypotheses and generating predictions. In this case, the modeling enhances understanding of the system but does not replace it. Increased understanding can arise only from simplifying the model. Therefore we need a suite of models, each designed to address a specific biological question.
Nature is awash in patterns that arise as organisms grow, develop and interact with their environment. The human brain is closely attuned to the beauty of these patterns—from butterfly wings to the coloration of flowers—and generations of scientists have been inspired, like D'Arcy Thompson, to look for their precursors and the underlying processes that give rise to nature's intricacy and order.
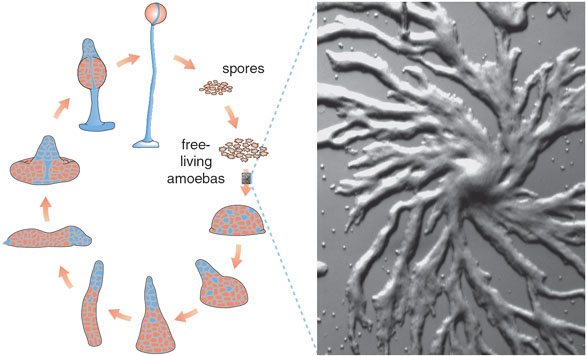
Illustration by Elyse Carter. Aggregation image courtesy of Rick Firtel's laboratory at the University of California, San Diego.
The organism that has produced the gold-standard model of pattern formation is not, though, a lovely flower or butterfly, but rather the lowly slime mold, Dictyostelium discoideum. "Dicty," as biologists in the field call it, is easy to culture and grow and accessible to genetic manipulation, and its functional and behavioral repertoire encompasses many aspects of biology that are important to human health and development. But what makes Dicty most interesting to model builders is its life cycle.
Dicty is a single-celled amoeboid organism about 10 micrometers (millionths of a meter) in diameter. Its food consists of bacteria, which leave trails of folic acid as they move about. Dicty is one of many microorganisms that move along sensed chemical gradients, a phenomenon known as chemotaxis. The slime mold finds its food by following folic-acid trails; it also secretes a substance that signals other Dicty cells to move away, presumably to leave each individual plenty of room to feed.
But when the food supply becomes scarce, Dicty cells reverse course and come together, aggregating to form a "slug" containing as many as 100,000 cells. As the slug takes shape, cells differentiate into two types, prestalk cells on one end and prespore cells on the other. About 20 hours after the start of aggregation, the slug forms a fruiting body, resting on one end while the prestalk cells migrate through the prespore region to form a stalk and push the developing spores upward. The spores are eventually carried by wind and other elements to another location, where they develop into new amoebas and begin the cycle again.
This is a remarkable and pictorially stunning story. A starving Dictyostelium colony aggregates by forming spiraling streams that slowly merge into a central mound, a pattern reminiscent of spiral galaxies. At this stage, Dicty cells secrete cyclic adenosine monophosphate or cAMP, a nucleotide best known as a "second messenger" in mammalian physiology. Through chemotaxis, cAMP drives the aggregation process: Cells can be seen to extend pseudopodia in the direction of increasing local cAMP concentrations.
Once the role of cAMP signaling in chemotaxis was elucidated, physicist and molecular biologist Evelyn Fox Keller and the late Lee Segel, an applied mathematician, began working at the Sloan-Kettering Institute to understand the dynamics underlying the spiral patterns and the aggregation process, which previously had been thought to come from some sort of community organization induced by signals from a few "pacemaker" cells. In other words, a few elite cells had been thought to rally the rest of the cells to secrete cAMP, leading to mass aggregation via chemotaxis. There was no experimental basis for this hypothesis at the time, and indeed the "pacemaker" cells could not be found.
Keller and Segel explained this pattern-formation process in a novel way. Extending to a cell-chemical system the idea that pattern could emerge through self-organization, they wrote down a model of chemotactic cell movement and signaling, incorporating aspects of reaction, diffusion and advective processes. With this model they showed that aggregation indeed results from an instability brought about by a tug-of-war between chemotaxis and diffusion—and proved that no "pacemaker" cells were needed.
This example illustrates that it is the integration of processes that leads to biological structure and function. Traditional biological reductionism cannot uncover the insight that is gained by mathematical modeling of how processes interact. At the same time, without reductionist approaches to determine what the individual elements of a system are, mathematical modeling risks being no more than building castles in the air. Molecular biology took Humpty Dumpty apart; mathematical modeling is required to put him back together again.
The Keller-Segel model consists of two coupled partial differential equations. The first describes the cells' bulk collective movement in the absence and presence of chemotactic stimuli. It models cells in analogy with charged Brownian particles in an electric field. Such particles perform a random walk biased in the direction of the field. In this case the particles are the cells, and the field is a chemical field; the Brownian motion (diffusion) qualitatively captures the cells' haphazard movement, and the biased random walk is a good analogy for chemotaxis. The second equation is a reaction-diffusion equation describing temporal changes in the cAMP concentration owing to the chemical's diffusion, decay and production by the cells.
Advances in biotechnology have made it possible to build more-sophisticated mathematical models describing how cells internalize and respond to the cAMP signals. A central component in these models is a Keller-Segel type of chemotactic response.
The Keller-Segel model has been modified and applied to many types of pattern formation that involve migrating cells: the process of angiogenesis during tumor growth, the formation of plaques in Alzheimer's disease and the elimination of foreign bodies by white blood cells. It remains the foundation of modeling at the supercellular level.
If cancer could be described with a pair of beautiful equations, medicine might be well on the way to finding a cure. But the malignant cell does not yield its secrets so readily. Cancer progression involves events taking place and interacting with one another on a wide range of length and time scales.
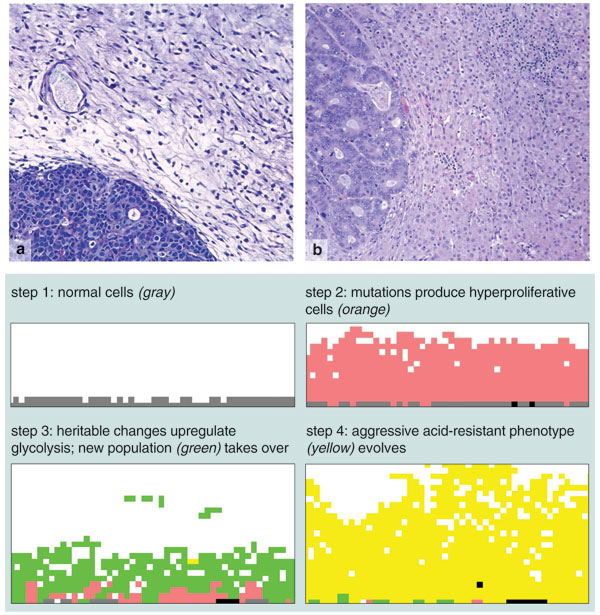
Images courtesy of Robert Gatenby, University of Arizona. Illustrations by Rosalind Reid.
Cancer usually begins with a series of genetic mutations. A scientist modeling cancer needs to know how mutations affect cells and how many mutations are needed before a cell escapes the normal controls on proliferation and death—and then how the mutant cell population begins to grow and escape additional anti-proliferative signals at a larger scale. As it grows, the mass of cells must overcome physical constraints; the cells will start to run out of oxygen, activating biochemical pathways that trigger the release of growth factors that hijack the body's blood supply. In this next stage, angiogenesis, blood-vessel linings break down, endothelial cells migrate toward the tumor, and blood vessels re-form, providing the tumor its own blood supply, access to nutrients and a pathway for invading other parts of the body.
In building a cancer model, it is tempting to simply include everything at every level. The resulting computations, unfortunately, might take longer to run than we have time left on the planet. The model would be burdened with a huge number of unknown parameters; we would simply have replaced a biological system we cannot understand with a computational system we do not understand.
Should we even try a mathematical approach? Of course we must; the potential benefits are enormous. Most drug treatments for cancer are designed to attack one aspect of the disease—say, angiogenesis. A multiscale model would allow us to explore the effects of combination therapies, approaches that attempt to stop cancer in its tracks by barricading multiple pathways. Most present models, focusing on processes at a single scale, cannot provide this comprehensive view.
The experience to date suggests two approaches to modeling a problem as complicated and multidimensional as cancer. One is to build a series of models that are essentially cartoons describing what is known at each level using the simplest equations possible. In physics, simple models have proved very successful; likewise the construction of simple models has been a fruitful tool for elucidating complex phenomena in biology. Such simplifications make computations tractable, but it's extremely difficult to know that you haven't, in building each model, made simplifying assumptions that threw out the key process.
Another approach is to follow in the footsteps of Turing, Keller and Segel: Ask a single question that suggests an entirely new model.
Robert Gatenby, a physician and mathematical biologist now at the University of Arizona, and Temple University physicist Edward Gawlinski have been asking just such a question about cancer. In recent work, Gatenby and Gawlinski stripped the cancer-modeling problem down to this question: "How can one population overcome another population?" In the context of cancer, this question has just three possible answers: Either you reproduce more, or you kill the other population, or both.
How can a population of mutant cells overcome a population of normal cells? The answer is not obvious. Under normal circumstances the pH in the body is such that it favors normal tissue slightly over cancerous tissue. In addition, cancerous cells tend to undergo anaerobic metabolism, which is almost 20 times less efficient than aerobic metabolism. (For this reason normal cells use aerobic metabolism, except under extreme circumstances.) Based on these simple facts, it would seem that the ability of cancer cells to compete effectively with normal cells violates the principles of evolutionary fitness. In Darwinian terms, cancer cells should not survive the selection pressures at work in the body.
Something else must be happening, and so Gatenby and Gawlinski have looked for sources of selective advantage. They noted that one byproduct of anaerobic metabolism is lactic acid. By producing lactic acid, cancer cells may change the pH of their environment so that it is poorly tolerated by normal cells. Could this convey an advantage large enough to give victory to cancer cells in a competition with normal cells?
To answer this question, Gatenby and Gawlinski wrote down a model to describe the spatiotemporal evolution of the two cell populations and lactic acid. In their model, the cancerous cells produce lactic acid, which in turn increases the death rate of normal cells. Under normal circumstances, normal cells "win," but the lactic acid effect gives the advantage to the tumor cells. Such simulations are effectively versions of a Lotka-Volterra model with cells standing in for predators and prey.
Gatenby and Gawlinski's model has already produced some provocative results. In certain parameter regimes, the stable steady state is one in which one population survives and drives the other to extinction—something known in ecology as the principle of competitive exclusion. In this case, getting rid of the dominant population (the cancer cells) is possible only if you remove all of that population; if you leave even a tiny fraction of it, the population will recover. Therefore the only effective way to remove the dominant population is to change the parameters so that you move to a regime where the dominant state is different. Put another way, the competitive model says that certain cancers cannot be cured by simply cutting them out, but could be cured by a combination of surgical removal and a treatment that will make the normal cells better competitors.
When one adds spatial diffusion to such a model, the solution takes the form of a traveling wave, just what Fisher saw when modeling the movement of an advantageous gene through a population: That is, a population moves through space with a profile that does not change in time.
With two competing populations (here, normal cells and cancer cells), the model produces two traveling waves, the dominant population advancing and the inferior population retreating. Typically populations in reaction-diffusion models overlap. However, the movement rules adopted by Gatenby and Gawlinski produced a different phenomenon—a gap between the advancing wave of cancer cells and the retreating normal cells. The fact that a so-called hypocellular gap is often found around tumors suggested that the modeling approach is on the right track. Further work involving one of us (Maini) has determined regions in parameter space where a cancer wave will not invade.
Gatenby is now exploring the nature of the observed gap in experiments. The model poses a specific challenge to experimentalists: Can they modify the parameters of the biological system so that it occupies the same range as the model system? Such manipulations would test the validity of the model. We are also, with a combination of modeling and experiment, exploring the idea that as a tumor population progresses, mutations are selected that enable malignant cells to survive in an ever more competitive and hostile environment.
If you simply want to determine whether modeling can help answer a question about the effectiveness of a treatment, a useful approach is to construct a supermodel from smaller submodels—models treating different scales and phenomena—to create a coherent abstraction of reality. This line of research, more closely related to engineering, has many practical applications.
One of us (Schnell) has been engaged in a cancer-modeling project based on the genetic and molecular features of the evolution of colorectal cancer. In building this model, Schnell and his coworkers have attempted to couple cellular and genetic factors while also accounting for the environmental factors regulating tumor growth.
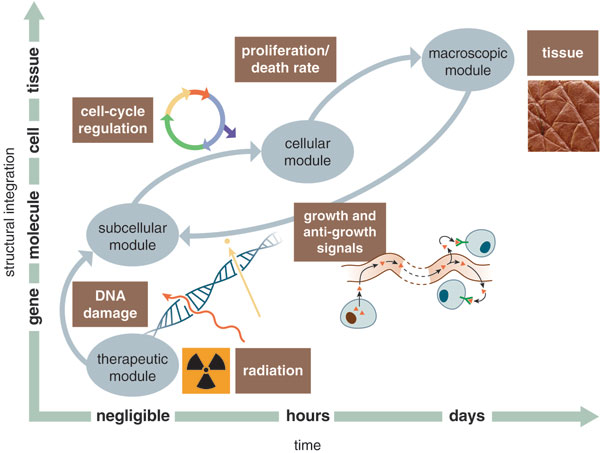
Illustration by Barbara Aulicino. Photograph by Eye of Science/Photo Researchers, Inc.
We now have a good deal of information about the genetic mutations underlying colon cancer and how activation of the mutated genes is affected by conditions of oxygen starvation (hypoxia) and overcrowding. We can model the life cycle of the cell—quiescence, division, death—and how it is influenced by these environmental changes.
Colon cancer is often treated with radiation because cancer cells are always proliferating more rapidly than other cells, and breaking double strands of DNA with radiation can kill cells that are undergoing division. Since it is known that radiation is most effective during a specific phase of the cell cycle, the team built a model to predict what proportion of the cells would be sensitive at different stages of tumor evolution.
We created a simulated tissue seeded with a number of small tumors. In this model, radiation doses are effective when administered before hypoxia and overpopulation begin to affect the cells, but radiation administered after a tumor reaches an oxygen-starved condition has little effect because most of the cells have become quiescent.
At the moment, this model does not make any predictions that doctors can use, but we hope that it can provide a tool for experimentation. Radiation is administered now using extensions of a 20-year-old model that assumes that tumor sensitivity and population growth are constant during radiotherapy. We now have the computational power and the genetic knowledge to incorporate a more up-to-date understanding of tumor dynamics.
We've presented here just a snapshot or two of modeling at work. A few further examples will convey the dynamic nature of the research going on around us and the rapid pace of change in our field.
An interesting aspect of current work is that both cancer-modeling approaches end up collapsing subcellular, cellular and supercellular processes into a simulation of a particular early stage of tumor growth that plays out in two dimensions (as shown in Figure 6). This is a type of simulation called a cellular automaton, built by assigning a set of rules governing the behavior of the cells on an artificial spatial grid.
Cellular automata have drawbacks and limitations: Interactions among cells on a uniform two-dimensional grid are a rather poor approximation of life. And cellular automata do not easily lend themselves to analytic calculations. More realistic grid-free approaches do exist, but they are currently not as popular as their grid-bound cousins.
Statistical physics provides additional useful frameworks: Many-body theory (the theory governing the interactions of multiple physical entities in a space), widely used in condensed-matter and quantum physics, provides techniques for building microscopic models of the random mutual interactions of many particles. One of us (Grima) has recently used this methodology, with cells standing in for particles, to bridge models at the opposite ends of the multiscale spectrum in biology.
At one end—the microscopic—models describe individual cell movement and interaction; a grid-free approach describing the position and velocity of individual chemotactic cells and molecules is such a model. At the other end—the macroscopic—models describe the dynamics of whole populations of cells. An example here is the Keller-Segel model, describing changes in the average concentrations of cells and substances. It turns out that the macroscopic model of slime-mold aggregation can be derived from the microscopic model only when the concentrations of cells and chemicals are particularly large and when the interactions between cells are weak to moderate. Otherwise a macroscopic model can fail to predict the correct behavior altogether. This result reinforces the fact that a model's validity is determined not only by the scale at which it appears to describe phenomena but also by other assumptions, which usually require derivation from finer-scale models. Determining a model's range of validity is crucial for successful modeling of any biological system.
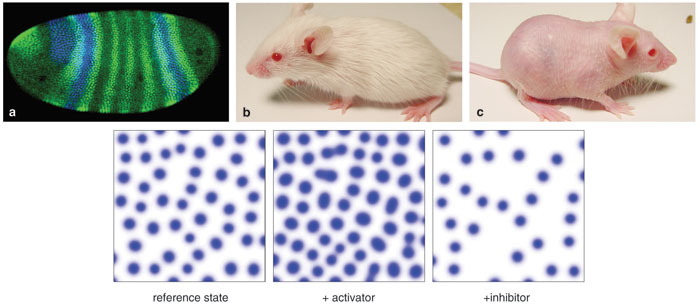
Drosophila laser-scanning confocal microscope image courtesy of Jim Langeland, Steve Paddock and Sean Carroll, Howard Hughes Medical Institute, University of Wisconsin–Madison. Additional images from Sick et al. 2006, reprinted with permission from the American Association for the Advancement of Science. Illustrations by Rosalind Reid.
The history of mathematical modeling in biology is one of spectacular successes and equally spectacular failures—sometimes involving the same approach. In some cases, modeling failures have revealed that the biological hypothesis underlying the model is incomplete. Turing's elegant work appeared to suffer a mortal blow when it was found that one of its most common applications—those spots and stripes—was flawed. In the early development of the fruit fly Drosophila, a series of seven stripes appear, expressing the so-called pair-rule genes. These stripes looked like an ideal application of the Turing model until biologists discovered that they could genetically knock out each expression stripe, leaving the others untouched. Each, then, comes about independently, a pattern that has been shown to arise from a number of simple gradient patterns influencing the expression of proteins in a cascading fashion.
But the Turing model has just recovered with a dramatic success—work published in Science in December 2006, confirming that hair-follicle patterns can be modeled as a reaction-diffusion process with short-range activation and long-range inhibition. Stefanie Sick at the Max Planck Institute of Immunology and her colleagues were able to manipulate a pair of mouse genes to show the mechanism at work.
It is an exciting time to be a mathematical biologist, or a practitioner of systems biology, as the reborn field has come to be known. The use of mathematical ideas, models and techniques is rapidly growing and increasingly important throughout the biosciences. The development of new programs has eliminated the well-demarcated divide between theory and experiment. The culture of biology is changing with a growing awareness that, as a colleague recently put it, "to think is to model." But verbal modeling does not allow us to compute the complex nonlinear and feedback interactions that characterize biological systems; for that we need mathematics. Before the rapid development of molecular biology, the field was largely qualitative; today no aspect of biology can afford to disregard quantitative measurement and analysis as too boring, time-consuming or difficult. Theorists and experimenters are now even working in the same buildings.
Understanding biological systems presents not only a scientific challenge, but also a social one in the monochrome, discipline-bound academic environment in which much of this research is being carried out. A diversity of epistemological approaches and a breaking of boundaries will be needed for the spectacular successes of modeling in biology to continue.
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.