Secrets in the Shell
By Roberto Ballarini, Arthur H. Heuer
The body armor of the queen conch is much tougher than comparable synthetic materials. What secrets does it hold?
The body armor of the queen conch is much tougher than comparable synthetic materials. What secrets does it hold?

DOI: 10.1511/2007.67.422
Queen conch (Strombus gigas) make tasty fritters, seviche or chowder, but before you can start cooking you have to extract the meat from the shell. This is not easy. Conch fishers suggest striking the shell between the third and fourth whorl on the turret with the sharp tip of another conch.
If you don't have another conch, you are advised to use "a hammer, hatchet, or better yet a machete," according to one guide. Whatever you do, it must be done expeditiously, or the conch will slime you in self-defense. Some would-be conch gastronomes, finding it all too much, just toss the whole creature in boiling water or a campfire and then pull the dead animal out of its shell with a fork or a stick.

Macduff Everton/Corbis
Strombus gigas means "giant spiral shell," an apt name for an animal whose magnificent defensive adaptation so frustrates lovers of seviche. Juvenile conchs, whose shells are still relatively weak, hide in the sand, emerging furtively at night to avoid the spiny lobster, blue crab, horse conch and 20 other predators that have a taste for mollusk meat. But by the time the conch is three years old, its shell is thick enough that it can graze amid beds of sea grass with little fear of molestation. True, a loggerhead turtle might crush the shell in its massive jaws or an octopus penetrate the shell with its barbed tongue and slip the conch a neurotoxin, but few of its predators are so equipped. The shell, though not impregnable, does such a good job of protecting its inhabitant that, once well-housed, a conch may live for 20 or more years.
Its success is the result of eons of attempts to make body armor that can resist the snap of a jaw or the scissoring of a claw. This endless adaptive tinkering has produced a material remarkable above all else for its toughness. The toughness arises not from the substance of the shell, which is made mostly of calcium carbonate (both ordinary chalk and the crumbly stuff found in over-the-counter antacids are 100 percent calcium carbonate), but rather from the "microarchitecture" of the shell, which involves crystallites of calcium carbonate sheathed in protein and bundled into criss-crossing beams. This microarchitecture assembles itself as the shell grows and can repair itself if the shell is damaged. However interesting in its own right, conch shell also suggests new ways to improve the properties of synthetic materials ranging from artificial bone to high-temperature ceramic composites.
Natural history is replete with solutions to the problem of making a structural material out of calcium-containing minerals, solutions invented and tested by the gradual trial-and-error process of evolution. The shells of turtles, bivalves, snails and other sea creatures solve this problem in a variety of ways, but all are composite materials (as are mammalian hard tissues such as teeth and bone).
Stephanie Freese
Composites achieve superior performance by combining materials that have complementary properties, such as mud and straw. Dried mud alone is weak in tension but strong in compression. Straw, on the other hand, is strong in tension but weak in compression. However, mud bricks made by mixing straw into the mud have a good combination of properties and are good building materials.
Shell is a composite of calcium carbonate and protein. Sheets of hard but brittle calcium carbonate are separated by thin layers of protein, a much softer and more pliant material. The calcium carbonate gives the shell stiffness and strength, and the protein between these mineral sheets not only provides some compliance, but also enables the shell to develop energy-dissipating microcracks that make it much harder to break. Properties superior to those of either material emerge from combining their different responses to mechanical loads.
The calcium carbonate produced by organisms can come in any of three crystalline forms—calcite, aragonite and vaterite. These polymorphs have slightly different atomic arrangements and can produce crystals with different external forms, depending on the environment in which they grow. Most turtle shells are vateritic and less mineralized than mollusk shells, but this form is otherwise rare. The mollusks, whose shells can be as heavily mineralized as tooth enamel, are split fairly evenly between aragonitic and calcitic forms of calcium carbonate. For example, abalone shell contains both calcite and aragonite, but conch shell is pure aragonite.
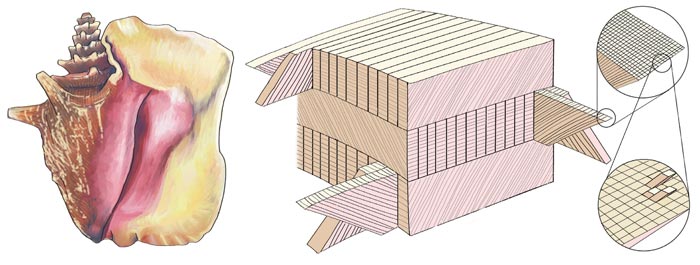
Another variable in shell design is microarchitecture. Shell structures at the microscopic level were first categorized by Danish scientist O. B. Boggild in 1930, but only a few examples—the nacreous and prismatic microstructures of abalone shells and the crossed-lamellar microstructure of conch shells—have been studied in depth using modern techniques. Nacre, or mother-of-pearl, is made of many thin sheets of calcium carbonate interleaved with layers of organic "glue," arranged like bricks in a wall. By contrast, the crossed-lamellar structure consists of criss-crossed sheets of calcium carbonate separated by protein layers, and is akin to plywood, a familiar wood/adhesive composite. As in plywood, the orientation of each sheet is at right angles to the ones above and below it.
The basic building block of the crossed-lamellar shell is a tiny plank of crystalline aragonite encased in a protein sheath. These crystallites are bundled into sheets called lamellae, and the lamellae are stacked together to form layers. The crucial characteristics of this architecture are that it includes elements with many different length scales and that, at each length scale, each structural element is rotated 90 degrees from the neighboring elements. In terms of its superior attributes, the crossed-lamellar structure represents the pinnacle of molluscan evolution, and most of the largest mollusk shells have this architectural motif.
Conch shell is at least 1,000 times tougher than mineral aragonite but only slightly stronger. "Strength" and "toughness" are used interchangeably in colloquial English, but they mean very different things to a materials engineer. The strength of a material is a measure of the force per unit area it can resist, be it stretched, compressed or flexed. Toughness is a measure of the amount of energy, or work, required to break the material into two pieces. So if the shell is tough, a predator must work very hard to break the shell and get the animal. Clearly, the conch needs to maximize the toughness of its shell; strength is somewhat secondary. The shell is unlikely to be pulled apart or squashed, but the conch must constantly beware of a sharp-toothed bite.

Photomicrographs courtesy of the authors.
The toughness of the shell arises from the composite nature of its microarchitecture. Although the protein layers are relatively weak and compliant, they play a critical role in lending the overall structure its characteristic toughness. When force is first applied to the shell, the protein-containing regions between aragonite crystals develop very useful, noncatastrophic microcracks. Such microcracking toughens the structure by dissipating the energy of mechanical forces. The cross-lamellar architecture itself provides a second energy-dissipating mechanism. Because alternating sheets of lamellae are at right angles to each other, cracks can only propagate through the material by following a tortuous zig-zag path, which requires much more energy to achieve a complete fracture.

Photograph at left © Jurgen Freund/naturepl.com. Photograph at right © Doug Perrine/SeaPics.com.
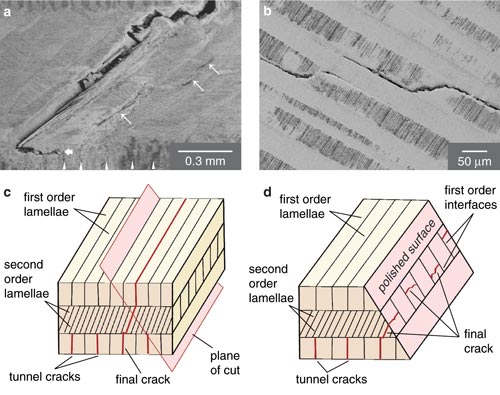
The inner layer of a conch shell exploits the first energy-dissipating mechanism to perfection. As force is applied to the shell ("loading it" in the parlance of engineers), more and more microcracks begin to open along the weak, vertical interfaces in this layer. These microcracks "tunnel" along the inner layer, meaning they travel along the axis of that lamellar sheet. However, because the orientation of the middle layer is in a different plane, the cracks can't spread. Instead, they are arrested at the interface between the inner and middle layers of the shell. This architecture allows "graceful" failure by making it difficult for a single crack to propagate completely through the shell.
According to a theoretical model we have developed, the inner layer will form many energy-dissipating microcracks as long as the middle layer of the shell is at least two times tougher than the protein interfaces. By testing conch-shell specimens, we determined that the ratio of fracture toughness between the inner and middle layers was usually about four. Given this ratio, our calculations revealed that the cracking of the inner layer alone was increasing the work required to fracture the shell by a factor of about 20 compared with abiogenic (mineral) aragonite.
If a predator bites down hard, however, one or more of the inner-layer cracks will eventually start to grow through the middle layer along a 45-degree interface between layers. Within the middle layer, however, the crack in one sheet of aragonite is impeded by the over- and underlying sheets, whose "grain" runs perpendicular to the axis of cracking. In order for the crack to spread, the adjacent sheet must deform against its neighbors to strain the aragonite beams of which the sheet is made. During the mechanical loading, lamellae with the favorable orientation also begin to microcrack, but the interleaving sheets with the unfavorable orientation remain intact. They thus "bridge" the crack and hold the shell together until the strain builds to the point that failure can occur. The structure is similar to reinforced concrete in some ways, except that brittle aragonite stands in for strong, ductile steel.
Photomicrographs courtesy of the authors. Diagrams adapted by Stephanie Freese.
This obstacle course of perpendicular sheets in the middle layer of the shell dissipates even more strain energy than the tunnel cracking of the inner layer. By polishing away the outer layer of slabs of shell, we were able to test the load-displacement properties of the middle layer specifically. We then used those data to develop a computer model that predicts how cracks spread in the middle layer. Our computational model suggests that together, the tunnel cracking and crack-bridging mechanisms increase the work of fracture about 330 times—in other words, it takes at least 330 times more work for a loggerhead turtle to break a conch shell than it would to break a similar structure made of mineral aragonite. Other experiments suggest that the work of fracture of the conch shell is closer to 1,000 times higher than that of mineral aragonite, raising the possibility that additional energy-dissipation mechanisms are still to be identified.
How exactly does the queen conch manage to create the exquisite structure of its shell? The secrets of shell deposition are just beginning to yield to inquiring bio-mineralogists, materials scientists and molecular biologists, but it is already clear that the process is complex. This is hardly surprising. Any adequate theory must be able to explain how the growth of the calcium carbonate crystals is initiated, what determines the type of calcium carbonate crystal that forms and how the crystal orientation and direction of growth are controlled.

Drawing adapted by Stephanie Freese. Photomicrographs courtesy of the authors.
The shell is synthesized by a specialized tissue called the mantle, a snug covering that encloses the head and foot of the snail like a fleshy sock. Shell growth occurs in two stages. In the first stage, a thin, transparent sheet of protein called the periostracum emerges from a fold in the mantle that is close to the shell opening and curls out and around to the outside of the shell. This living "drapery" creates a pouch at the edge of the shell called the extrapallial space, so named because it is below the pallial line where the mantle attaches to the shell. New shell is deposited in this protected microenvironment. The cells of the mantle epithelium secrete proteins into the extrapallial space, together with the calcium and bicarbonate ions that will combine to form calcium carbonate.
The research group led by one of us (Heuer) has gained some insight into shell development through experiments on wound repair. In these studies, we manually stimulated juvenile conchs to make the mantle withdraw from a region of shell, drilled a 4-millimeter-wide hole, taking care to avoid the edges of the shell, then covered the wound with a thin (0.2 millimeter) plastic lid to limit the loss of nutrients. As the hard tissue regenerated over the next week and a half, we studied its progress using a scanning electron microscope.
The initial stage of wound repair involved deposition of a transparent membrane; the first crystals deposited on the plastic lid are shown in Figure 6b (the arrow shows some organic matrix, the protein glue that holds the crystals together). Similar crystal aggregates embedded in the organic membrane on the mantle side (rather than the lid side) of the regenerated tissue are shown in Figure 6c. Only later, about eight days after the hole was drilled, did the conch begin to lay down the orderly structure of normal shell. In a sense, the disordered layers served as a scab, a temporary scaffolding formed to allow the slower but more permanent repair process to commence.
A cross section of the regenerated hard tissue, as seen in Figure 6d, reveals that a layer of vertical crystallite precedes the development of the crossed-lamellar structure. This sequence is exactly what happens during normal shell formation, in which a layer of vertical crystals forms on the periostracum before the crossed-lamellar microarchitecture begins to form. Figure 6e shows the inner layer surface of the fully healed wound after 10 days. The comparable but better-developed texture of "wild" shell is shown in Figure 6f.
The geometry of pearlescent nacre is simpler than that of the crossed-lamellar architecture of the conch shell, and its deposition has been studied in abalone shell in the laboratory of Daniel E. Morse at the University of California, Santa Barbara, for more than 10 years. Abalone nacre has much the same structure as a brick wall, but one with very thin bricks. All nacreous structures shimmer with color because the calcium carbonate bricks are comparable in thickness to the wavelengths of visible light, which they thus diffract and scatter.

Diagrams adapted by Stephanie Freese. Photomicrograph b courtesy of the authors. Photomicrograph c courtesy of D. E. Morse
For many years, scientists thought nacre was made the way we would make a brick wall: The mollusk would secrete a layer of protein, analogous to a mason's cement, which would somehow promote the crystallization of calcium carbonate. Then the animal would lay down another layer of protein that would cap the crystal. A new layer of crystalline minerals would form on the new protein, and so on. But this isn't the way it turned out at all.
Morse's team was surprised to find that the actual mechanism is different and much more interesting. They found that mineral crystals do grow on a nucleating layer of protein, but their growth is guided by the secretion of 20 to 30 additional proteins. At the molecular scale, these proteins interact with the growing crystal and determine the form of calcium carbonate and the orientation of the crystal axes (the direction in which the microcrystals are growing). In abalone, as in conch, the first crystals to form on the periostracum are vertically aligned, resulting in a so-called prismatic structure. But these first crystals are the calcite form of calcium carbonate. Further growth of the shell occurs by the formation of aragonitic nacre.
Using an atomic-force microscope, the team was able to directly observe changes in the atomic lattice—the basic arrangement of atoms in the crystal—when they introduced certain soluble proteins. These proteins triggered the abrupt shift from the calcite polymorph to the aragonite polymorph.
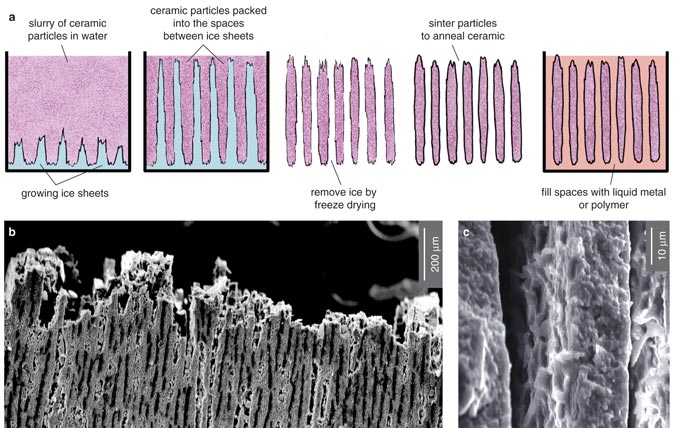
Illustration by Christopher Brodie and Stephanie Freese. Photomicrographs courtesy of E. Saiz.
At the same time as it is releasing these soluble proteins, the mantle also secretes insoluble proteins that become a permanent organic framework containing voids into which the crystals will grow. These proteins assemble themselves into thin walls and chambers that are pocked with small pores. As the crystals form in this labyrinth, instead of each mineral block being capped by a layer of protein (the bricklayer model), the crystals grow continually through the tiny pores, each some tens to hundreds of nanometers wide, from one void in the protein matrix to the next.
The remarkable chemistry that creates this organic matrix gives this type of shell its strength. Just as a brick wall is structurally robust because courses of bricks are offset from one another, nacre obtains its impressive load-bearing ability because each layer of crystals is offset from the next. But in abalone shell, unlike human-built walls, the offset arises because the pores in the protein sheets are randomly spaced and do not align with those in neighboring sheets. The disconnect between the well-executed result and the chaotic means by which it is achieved suggests just how different nature's manufacturing technology can be from our own.
Certainly it seems daunting to duplicate the natural process of shell deposition, with its long list of crystal-modulating proteins. Scientists have tried instead to reproduce the microarchitecture of nacre by simpler means—bioinspiration as opposed to biomimicry. But early attempts produced too few layers or layers that were too thick, and there were problems as well with the bond between the stiffer layers and the organic adhesive.
Adapted from White et al. by Stephanie Freese. Photomicrograph courtesy of N. R. Sottos, reprinted with permission from Macmillan Publishers Ltd: Nature.
Recently, scientists at Lawrence Berkeley National Laboratory created layered ceramic composites similar to nacre using a clever method that solves some of these problems. The scientists took their inspiration from a unique phenomenon that can happen when the sea freezes. As salt water becomes solid, the growing ice crystals sometimes form tiny treelike, or dendritic, plates. The salt that is expelled from the ice crystals becomes trapped within channels between the plates. The investigators, led by Antoni P. Tomasia, saw that they could exploit this natural process to make a variety of "ice-templated" ceramic composites with the microarchitecture of nacre.
The team mixed water and ceramic powders and then froze the slurry from the bottom up. The temperature gradient caused the water to form broad, flat crystals perpendicular to the freezing front. As the ice crystals grew, the ceramic and polymer were concentrated in the spaces between them. Later, the scientists freeze-dried the material to remove the water, sintered (heat-cured) the ceramics and then filled the voids with a second material, such as liquid metal or a polymer. In one example, they made synthetic bone composites by freezing a slurry of hydroxyapatite powder (hydroxyapatite is the mineral component of bone) and filling the voids with epoxy. Another experiment created a composite made of 45 percent aluminum oxide and 55 percent aluminum-silicon alloy. The resulting material had a strength-toughness combination superior to ceramic-metal composites made by other techniques.
The Lawrence Berkeley composites are much more finely layered than previous synthetic composites. By increasing the rate at which the water froze, the team found it could make the layers only 1 micrometer thick, which is comparable to the approximately 0.5-micrometer-thick lamellae in natural nacre. Moreover, the composites had other features that probably contribute to nacre's favorable mechanical properties, such as surface roughness comparable to that found in wild nacre—an attribute that helps the layers of the composite stick together. By borrowing a simpler, self-organizing phenomenon, the Lawrence Berkeley team was able to create the microstructure of nacre without duplicating nature's methods.
As discussed earlier, the self-assembly inherent in shell development leads to remarkable self-healing powers. Self-healing is as desirable a material property as self-assembly—how wonderful would it be to have self-healing potholes?—but equally difficult (if not more so) to achieve. A self-healing material must somehow sense it is damaged, attract healing supplies to the damaged area and initiate repairs that match the structure of the existing material. These are demanding specifications, but materials scientists are taking their first steps in this direction.
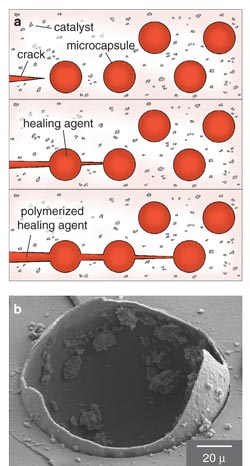
A team led by Scott R. White and Nancy R. Sottos of the University of Illinois at Urbana-Champaign devised a self-healing thermosetting polymer. Thermosetting polymers, a class of brittle materials widely used in microelectronic components and as aerospace materials, develop dangerous microcracks when subjected to repeated cycles of temperature and mechanical stress. To make self-healing composites, White, Sottos and their colleagues added to the composite material microcapsules filled with a healing agent (a polymer precursor) and veined the material with a polymerizing catalyst. When a crack ruptured one of the capsules, the precursor flowed into the crack, encountered the catalyst and glued the crack surfaces together. Remarkably, the healed composite retained nearly 75 percent of the original material's toughness.
Based on this success, it is possible that this approach to healing cracks in materials could eventually be replaced by a system that mimics biological structures by sensing and locating the damage, carrying some sort of healing agent to the damaged site and performing a healing procedure. Or perhaps an even more effective method awaits discovery. Certainly nature has important lessons for improving modern technology. But this should be accomplished through bioinspiration rather than slavish copying. Examples abound, but an obvious one is a hallmark of the modern age. We doubt that airplanes would have been developed had people not observed birds, but airplanes do not have flapping wings!
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.