Laser-Sharp Vision
By Catherine Clabby
A logjam, an interdisciplinary quest, and relentless refinement lead to a novel way to look at the world.
A logjam, an interdisciplinary quest, and relentless refinement lead to a novel way to look at the world.

DOI: 10.1511/2014.106.18
Penn State undergraduate Benjamin Hall started cutting slices of corn roots with a pulsing laser in 2012, thinking he was just helping streamline the tedious job of preparing plant samples for study. Little did he know he was pioneering a whole new imaging technique.
The corn-slicing project originated with a problem faced by Jonathan Lynch, a plant biologist on campus. Lynch is hunting for strains of corn that grow well in drought and substandard soils, traits that could help feed a growing global population in a warming world. To identify the most promising strains, Lynch’s laboratory studies, among other things, variation in structures inside corn roots. But prepping roots for microscopic study is labor intensive. One person can create only 30 to 40 sections a day. Lynch’s lab faced a backlog of more than 20,000 roots.

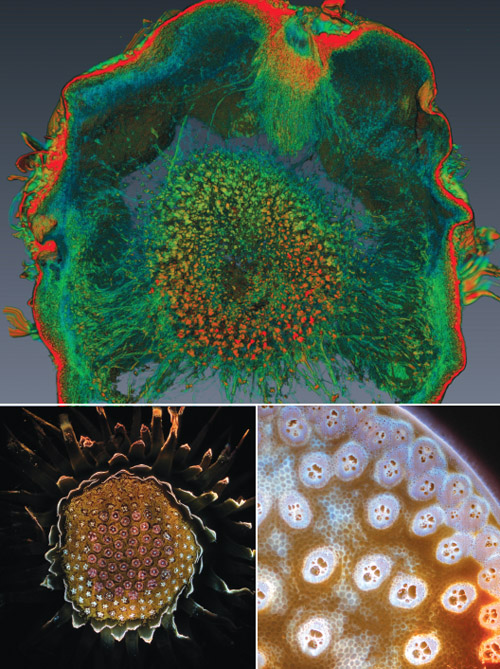
Image courtesy of Benjamin Hall.
At the Applied Research Laboratory at Penn State, Ted Reutzel runs a department that uses lasers to alter materials. When Lynch’s son inquired there if a laser could speed up Lynch’s slicing process, Reutzel handed the problem to Hall, an extremely curious student employee who is driven to solve puzzles. Following Reutzel’s advice, Hall explored what he could do with Penn State’s Q-switched ultraviolet laser—a device that can produce 10,000-watt light pulses just billionths of a second long.
Within a few days, Hall was wielding the laser to cut 11 root slices per second, each a consistent 0.1 millimeters thick. That was a major improvement, but the process of preparing the slices for inspection was still time-consuming. He still needed to collect the slices carefully, pack them up, and transport them to Lynch’s laboratory across campus. Once there, the pieces had to be mounted on microscope slides one by one for viewing and imaging, eating up more time.
Lynch immediately saw big promise in the laser technique for himself and for other plant biologists with sample backlogs. Lynch, Reutzel, and Hall obtained a $10,000 grant from the National Science Foundation’s Research Experience for Undergraduates to finance further development of the new sectioning system. “Initially we were just replacing the knife,” Hall says. “Then I spent many weeks playing around with this stuff in a constant effort to reduce the amount of work.”
Images courtesy of Benjamin Hall.
Hall started photographing the samples himself. A camera fitted with a high-magnification lens snapped away as the laser incrementally vaporized each root. In time he produced a series of digital cross-section views. Seen through a conventional, bottom-lit microscope slide, the colors of the plant slices were washed out. With the new imaging setup, the ultraviolet laser light caused tissues in the root to fluoresce in distinctly different colors, creating multihued and sharp images. The collaborators had made another step forward.
Looking for further efficiencies, Hall continued to automate the process. He placed roots on a movable platform so that after each laser blast, the sample’s surface moved to the same spot where it had been imaged previously. Then he switched from still images to digital movies that continually recorded the process. Using free software he downloaded from a National Institutes of Health website, Hall edited each movie into a series of still images that could then be stacked together into a three-dimensional reconstruction.
The technique displays more in the samples than can be observed through a conventional microscope. The three-dimensional views of the roots made internal structures, such as the water-conducting xylem vessels, clearly visible. On top of that, a much-needed increase in how quickly samples can be studied was attained. That is vital for Lynch, whose laboratory must observe large numbers of individual plant samples to hunt down which corn strains truly have drought-resistant traits. “People have been sectioning things by hand for a very long time,” Lynch says. “That was the bottleneck.”
The Penn State approach is broadly analogous to computerized tomography, or a CT scan. With CT scans, a series of X-ray views are taken from many different angles and then combined, with software, to create 3D images of bones and soft tissues inside a body. CT systems render images based on density variations that X rays capture in the sample under study. One limitation is that different materials with similar densities can be difficult to distinguish. The Penn State imaging technique can capture more detail than CT scanning. It destroys the samples it records, however, making it incompatible with studies of rare fossils, archaeological relics, forensic items, or live specimens.
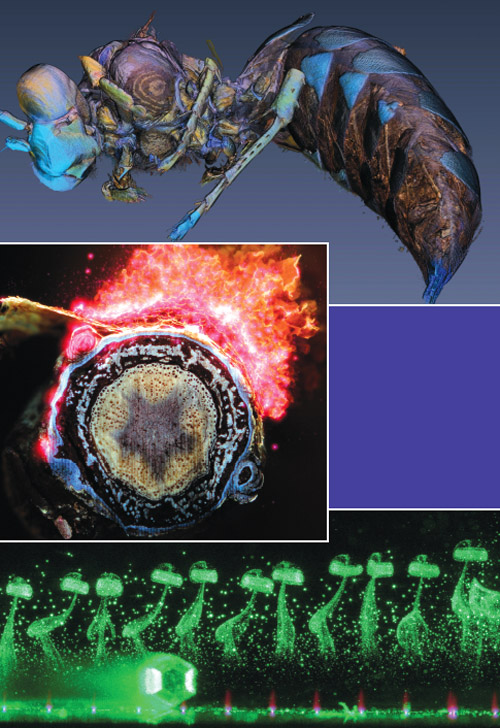
Images courtesy of Benjamin Hall.
Lynch and Hall are currently collaborating on a scientific paper describing the imaging technique, which Penn State is in the process of patenting. Meanwhile, Hall and former Penn State graduate student Brian Reinhardt have launched a company, Lasers for Innovative Solutions, to commercialize the technology. They will offer services to agriculture companies studying large volumes of samples to compare internal structures of different strains of plants.
Hall sees many more potential applications. The ablation technique could reveal the porosity and organic content of rock in regions where energy prospectors are using fracking (hydraulic fracturing) to extract natural gas, he says. Or it might reveal the internal circuitry in older but important electronic devices, assisting efforts to reverse engineer products for which no drawings or suppliers can be found. Hall is also enthused by the unforeseen applications he expects will emerge. The imaging technique itself, after all, is an unforeseen outcome of an interdisciplinary collaboration.
“That is one of the biggest lessons of my life,” Hall says. “It is so inspiring to be straddling the boundary of what humans know and don’t know.”
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.