Programming Your Quantum Computer
By Brian Hayes
The hardware doesn’t yet exist, but languages for quantum coding are ready to go.
The hardware doesn’t yet exist, but languages for quantum coding are ready to go.

DOI: 10.1511/2014.106.22
The year is 2024, and I have just brought home my first quantum computer. When I plug it in and switch it on, the machine comes to life with a soft, breathy whisper from the miniature cryogenic unit. A status screen tells me I have at my disposal 1,024 qubits, or quantum bits, offering far more potential for high-speed calculation than all the gigabits and terabytes of a conventional computer. So I sit down to write my first quantum program.

Photograph courtesy of the author.
And that’s where I get stuck every time I run through this daydream. I know a little about the basic principles of quantum computation, but I’ve never had a clear vision of what it would be like to write and run programs on a quantum computer. Can I express my ideas in a familiar programming language, with all the usual algorithmic idioms, such as loops and if-then-else statements? Or is the experience going to be completely new and alien—like quantum mechanics itself?
Most of what I’ve read tends to support the new-and-alien thesis. The protocol for solving a problem with a quantum computer is often described like this: Prepare a set of qubits in a suitable initial state, apply a specified series of operations, then measure the final state of the qubits. If all goes well, the measurement will yield the answer to the problem. To me, this process doesn’t sound like computer programming; it sounds like running a physics experiment. I yearn for some other way of describing the computation, closer to my accustomed habits of thought.
Evidently I am not alone in this sentiment. Several high-level programming languages for quantum computers have been developed, even though the computers themselves don’t yet exist. I have been exploring two of these languages, QCL and Quipper, which are surprisingly rich and full-featured. The languages provide a glimpse of how programming might be done when my kiloqubit computer finally arrives.
My complaint that quantum computation seems too much like a laboratory experiment is a little unfair. Classical computing has the same complexion if you examine it closely enough. Adding a column of numbers in a spreadsheet could be described as preparing a set of bits in the appropriate initial state, applying the summation operator, and measuring the final state of the bits. But no one thinks of the process in those primitive terms.
Computer science has evolved a hierarchy of conceptual layers that hide the details of layers below them. At the bottom are physical entities such as transistors and electronic circuitry. Next come logic gates (AND, OR, etc.), which operate on symbols ( true and false, 0 and 1) rather than voltages and currents. The gates are assembled into registers, adders, and the like; then an instruction set defines commands for manipulating data within these components. Finally, the details of the instruction set are hidden by the constructs of a higher-level programming language: procedures, iterations, arrays, lists, and so on.
Creating complex software would be beyond human abilities without the abstraction barriers that separate these layers. It’s just not possible to think about the design of a large program in terms of electric currents flowing through billions of transistors. As Alfred North Whitehead wrote, “Civilisation advances by extending the number of important operations which we can perform without thinking about them.”
But the barriers are seldom perfect. Modern processor chips have multiple cores that execute streams of instructions in parallel; a programmer cannot take full advantage of that parallelism without thinking about lower-level details. Thus civilisation retreats a little. Quantum computing, too, will surely trespass on some abstraction barriers.
Abstraction barriers break down because computers are not abstractions. A computing machine is a physical object, which has to obey the laws of nature as well as any rules of logic or mathematics that the designer wants to impose. You can’t entirely ignore the physical substrate—and that goes double for a quantum computer.
The bits of a classical computer are just binary digits, with a value of either 0 or 1. Almost any device with two distinct states can serve to represent a classical bit: a switch, a valve, a magnet, a coin. Qubits, partaking of the quantum mystique, can occupy a superposition of 0 and 1 states. What does that mean? It’s not that the qubit can have an intermediate value, such as 0.63; when the state of the qubit is measured, the result is always 0 or 1. But in the course of a computation a qubit can act as if it were a mixture of states—say, 63 percent 0 and 37 percent 1. Only a few physical systems exhibit superposition clearly enough to function as qubits. Examples include photons with two directions of polarization, atomic nuclei with two spin orientations, and superconducting loops with clockwise and counterclockwise electric currents.
Another key aspect of qubit behavior is interference, a phenomenon well known in the physics of waves. When two waves overlap, they can either reinforce each other (if the peaks and valleys of the undulations coincide) or they can cancel (if the waves are out of phase). Mathematically, the intensity of the combined waves at any point is given by the square of the sum of the individual wave amplitudes. When the two amplitudes have the same sign, the interference is constructive; when one amplitude is positive and the other negative, the resulting destructive interference yields an intensity less than that of either wave alone.
Like waves, the 0 and 1 states of a qubit have amplitudes that can be either positive or negative. (Actually, the amplitudes are complex numbers, with real and imaginary parts, but that complication can be ignored here.) Depending on the signs of the amplitudes, quantum interference can either increase or decrease the probability that a specific state will be observed when the qubit is measured.
Interference plays a role in all the interesting algorithms for quantum computers—that is, the algorithms that might enable such a machine to outperform a classical computer. The general idea is to arrange the evolution of the quantum system so that wrong answers are suppressed by destructive interference and right answers are enhanced by constructive interference. In this way the algorithms exploit a form of parallelism that’s unique to quantum systems. In effect, a collection of n qubits can explore all of its 2 n possible configurations at once; a classical system might have to look at the 2 n bit patterns one at a time.
One last aspect of quantum weirdness is entanglement. When two or more qubits interact, they may form a fused state that cannot be teased apart to show the contributions of individual qubits. In other words, you cannot poke around inside a quantum register and alter one qubit while leaving the rest undisturbed. Entanglement is a prerequisite for at least some of the important quantum algorithms.
Among those algorithms, the best known is a procedure for finding the factors of integers, devised in 1994 by Peter W. Shor, now at MIT. When factoring an n-digit number, the fastest known classical algorithms take an amount of time that grows exponentially with n; Shor’s algorithm works in time proportional to n3. For large enough n, the quantum algorithm is far faster.
The prospect of greater computing power in quantum systems is intriguing, but it comes with some awkward constraints. To begin with, every function computed by a quantum system must be fully reversible. If the machine grinds up input A to produce output B, then it must have a way to reconstruct A when given B. A corollary is that every function must have the same number of inputs and outputs. In one stroke, this rule outlaws most of arithmetic as conventionally practiced. The usual addition algorithm, for example, is not reversible. You can add 3 and 4 to get 7, but you can’t “unadd” 7 to recover the original inputs 3 and 4. To add reversibly, you must avoid erasures, preserving enough information to retrace your steps. Reversible methods exist for all computable functions, but they require some mental adjustments in one’s approach to problem solving.
Another no-no in quantum computing is copying a qubit. (This principle is called the no-cloning theorem.) Nor can you arbitrarily set or reset qubits in the middle of a computation. Attempting to do so would destroy the quantum superposition.
Any quantum program must have a stovepipe architecture: Information flows straight through.
Taken together, the restrictions on qubit operations imply that any quantum program must have a stovepipe architecture. Reversible quantum logic gates are lined up in sequence, and information flows straight through them from one end to the other. Of particular importance, the program structure can have no loops, where control is transferred backward to an earlier point so that a sequence of instructions is traversed multiple times.
Loops and conditional branching are indispensable tools in classical computer programming. How can we possibly get along without them? Anyone building a pure quantum computer will have to confront this difficult question. As a practical matter, however, the answer is: Don’t build a pure quantum computer. Build a classical computer with a quantum subsystem, then create appropriate software for each part. The quantum programming languages QCL and Quipper both acknowledge this reality, though in different ways.
QCL, or Quantum Computation Language, is the invention of Bernhard Ömer of the Vienna University of Technology. He began the project in 1998 and continues to extend and refine it. Ömer’s interpreter for the language (http://www.itp.tuwien.ac.at/~oemer/qcl.html) includes an emulator that runs quantum programs on classical hardware. Of course the emulator can’t provide the speedup of quantum parallelism; on the other hand, it offers the programmer some helpful facilities—such as commands for inspecting the internal state of qubits—that are impossible with real quantum hardware.
QCL borrows the syntax of languages such as C and Java, which are sometimes described as “imperative” languages because they rely on direct commands to set and reset the values of variables. As noted, such commands are generally forbidden within a quantum computation, and so major parts of a QCL program run only on classical hardware. The quantum system serves as an “oracle,” answering questions that can be posed in a format suitable for qubit computations. Each query to the oracle must have the requisite stovepipe architecture, but it can be embedded in a loop in the outer, classical context. During each iteration, the quantum part of the computation starts fresh and runs to completion.

Illustration by Brian Hayes.
An annotated snippet of code written in QCL is shown in the illustration at right. The procedure shown, which is taken from a 2000 paper by Ömer, calculates the discrete Fourier transform, a crucial step in Shor’s factoring algorithm. Fourier analysis resolves a waveform into its constituent frequencies. In Shor’s algorithm a number to be factored is viewed as a wavelike, periodic signal. If N has the factors u and v, then N consists of u repetitions of v or v repetitions of u. Shor’s algorithm uses quantum parallelism to search for the period of such repetitions, although the process is not as simple and direct as this account might suggest. The QCL program has a classical control structure, with two nested loops, and a quantum section that performs the actual Fourier transform.
The language called Quipper was developed in the past few years by Peter Selinger of Dalhousie University in Canada, with four colleagues. An implementation is available at http://www.mathstat.dal.ca/~selinger/quipper/.
Quipper is intended for the same kinds of programming tasks as QCL, but it has a different structure and appearance. The language is implemented as an extension of the programming language Haskell (named for the logician Haskell B. Curry), which adopts a functional rather than imperative mode of expression. That is, the language is modeled on the semantics of mathematical functions, which map inputs to outputs but have no side effects on the state of other variables. A functional style of programming seems more closely attuned to the constraints of quantum computing, although Haskell does not enforce the quantum rule that a variable can be assigned a value only once.
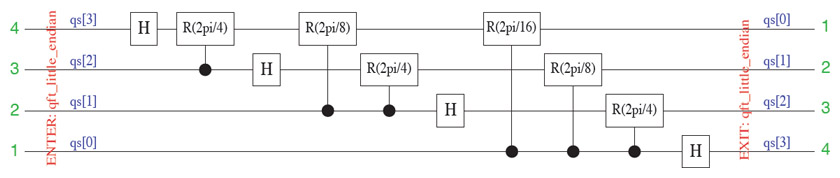
The Quipper system is a compiler rather than an interpreter; it translates a complete program all in one go rather than executing statements one by one. The output of the compiler consists of quantum circuits: networks of interconnected, reversible logic gates. A circuit can take the form of a wiring diagram, such as the one above, but it also constitutes a sequence of instructions ready to be executed by suitable quantum hardware or a simulator.
I find it mildly ironic that these avant-garde computers have brought us back to the idea of seeing programs as circuits, in which signals flow through long chains of gates. In the 1940s the ENIAC computer was programmed in a similar way, by plugging wires into panels. But Selinger points out there’s an important difference: We now have tools (such as QCL and Quipper) that generate the circuits automatically from a high-level source text.
Selinger and his colleagues set out to produce a practical, “scalable” system, suitable for more than just toy examples. They give solutions to seven benchmark problems, measuring the performance of their quantum programs in terms of the number of qubits needed and the number of gates in the circuits. They are able to handle large problem instances. One program requires 4,676 qubits and 30,189,977,982,990 gates. (They chose not to draw the circuit diagram with 30 trillion gates.)
Languages such as QCL and Quipper may well solve the problem of how to write programs for quantum computers. There remains the question of what programs to write. Stephen Jordan of the National Institutes of Standards and Technology maintains a “Quantum Algorithm Zoo” ( http://math.nist.gov/quantum/zoo/); it lists 50 problems that have interesting quantum solutions. That is not a large number, although some of the individual problems could have many applications. One example that covers a broad spectrum is the use of quantum computation to simulate quantum physics. This is where the whole field began, with a suggestion 30 years ago by Richard Feynman.
Of course all these questions remain academic until reliable, full-scale quantum computers become available. A company called D-Wave offers machines with up to 512 superconducting qubits, but the architecture of that device is not suited to running the kinds of programs generated by QCL and Quipper; indeed, there’s controversy over whether the D-Wave machine should be called a quantum computer at all. For technologies that can implement quantum circuits with controlled interference and entanglement, the state of the art is roughly a dozen qubits. With those resources, Shor’s algorithm can factor the number 21. Much work remains to be done before my kiloqubit laptop arrives in 2024.
©Brian Hayes
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.