This Article From Issue
January-February 2019
Volume 107, Number 1
When European soldiers, priests, tradesmen, and settlers first arrived in the New World at the end of the 15th century, they often expressed surprise about the large number of settlements they encountered.
From the point of view of many scholars nowadays, it’s unfortunate that these first Europeans do not seem to have made any reliable or comprehensive estimates of how many people were living in the settlements they encountered or even in entire regions they traversed; at least, no estimates have ever been found. To this day, archaeologists continue to struggle with estimating the number and distribution of indigenous people who were living in these lands before the era of European colonization.
Information of this kind would be extremely valuable for historians, archaeologists, and anthropologists studying the pre-Columbian human populations of the Americas. For example, certain areas of the Yucatán peninsula have yielded evidence that the ancient Maya invested great resources to make wetlands appropriate for growing corn, squash, and avocados. This finding, in turn, enables researchers to begin to form hypotheses about how and when agriculture was practiced at a given settlement. The inhabitants of this area were modifying the wetlands for agriculture, a feat that speaks highly of their hydrology and engineering skills as well as their degree of social organization. Moreover, they were doing so at a scale that allowed for the subsistence not only of the nearby settlements but also of tens of thousands of people who lived hundreds of kilometers away, a fact which provides additional evidence of extensive transport networks and complex systems of commerce and exchange.
Two approaches are commonly used to estimate historical variations in the precolonial population of the New World, but both approaches depend on incomplete and imperfect data. One approach consists of finding the earliest available population estimates from fragmented census documents and informal accounts, and then working backward in time using estimated rates of birth and mortality. A second approach uses archaeological data to estimate the populations of ancient hamlets, villages, towns, and cities, working with an assumed number of residents per structure.
Attempts to work back in time from population estimates made hundreds of years later cannot be trusted, because differences of only a few percentage points in assumed mortality rates result in estimates of the total population that differ by tens of millions. As a further complicating factor, a series of epidemics swept through the indigenous population of central Mexico, and perhaps through populations in other areas of the New World, in the century after the arrival of Europeans. The historical records that have survived from that time suggest that the population of central Mexico may have been reduced from about 25 million to 700,000 within a single century after the arrival of the Europeans. This figure is contentious, however, because archaeologists have no consensus on a starting point—that is, the size of the population at the start of the epidemics. Some experts consider it unlikely that the indigenous population of central Mexico was as high as 25 million in the year 1500 or so, whereas others argue that it may have been closer to 40 million. It has become common for researchers who differ markedly in such estimates to be tagged as either high counters or low counters. The low counters challenge the contention that tens of millions of indigenous people were living in the New World when the Europeans arrived, asking, “Where are the remains of the cities that would have been required to house so many people?” High counters offer two possible answers: that the extent and the population density of the known ancient settlements (including the surrounding suburbs and farmlands) may have been larger than heretofore realized, and that there may be ruins of additional settlements yet to be found.
If there are such undiscovered sites, or “lost cities,” as they are popularly termed, it may seem that locating and mapping their remains would be a comparatively simple matter in the Space Age. After all, NASA and military agencies routinely launch satellites containing high-resolution digital cameras with a wide range of wavelength sensitivities, as well as radar (radio detecting and ranging) and lidar (light detection and ranging) instruments. The satellites then use the round-trip travel times of short pulses of electromagnetic radiation (radio waves and laser beams) to compute vectors (direction and distance) from a transmitter to reflecting surfaces and create three-dimensional maps of the Earth’s surface.
Linear features, such as ancient roadways, walls, and irrigation canals that cut across the natural terrain, stand out particularly well.
The challenge is more complicated than it may seem, however. Satellite-based sensors can provide accurate images of today’s urban and unforested areas but can tell us little about the populations of centuries ago, because the patterns of land use and population distribution have changed extensively. And even the most advanced satellite-based observations haven’t enabled archaeologists to peer through the heavy vegetation in rain forests or jungles, because they suffer from the relatively large distances (tens to hundreds of kilometers) between the sensors and the surface to be mapped, as well as from the high along-track velocities of low orbit satellites. The large distances result in weak returns (reflections) from the surface of the Earth, and the high velocities make it extremely difficult to obtain coverage of the surface that is dense enough to derive bare-earth images with meter-level resolutions.
Photogrammetric mapping techniques, based on aerial photographic surveys, offer another possible approach. However, because they rely on solar illumination, they can’t provide information on terrain that is hidden beneath, or in the shadows of, dense forests.
One technique that successfully avoids all these pitfalls is airborne lidar. Recent advances in the technology of aerial surveying, together with the increasing use of airborne lidar, are leading to significant revisions in archaeologists’ thinking about the population and the social and political structures in the pre-contact Americas.
At the core of an airborne lidar system are one or more lasers that emit pulses of light with a typical duration of a few nanoseconds (10-9 seconds), at repetition rates that range from tens to hundreds of thousands of pulses per second. The laser pulses are distributed in two dimensions over the area of interest. The first dimension is along the flight line of the aircraft; the second is across the flight line and is obtained using an optical scanner (most often an oscillating mirror or rotating polygon). The motion of the aircraft, in combination with the optical scanning, distributes the laser pulses over a strip or swath of terrain. As the laser pulses travel away from the aircraft, some or all of them encounter vegetation, human-built structures, or the ground, reflecting photons back to the sensor. The reflected photons are registered by a photodetector, and a timing device determines the two-way flight times between the sensor and the reflecting surfaces. Dividing the flight time by two and multiplying by the speed of light yields the slant range, the straight-line distance from the transmitter reference point to the reflecting surface.
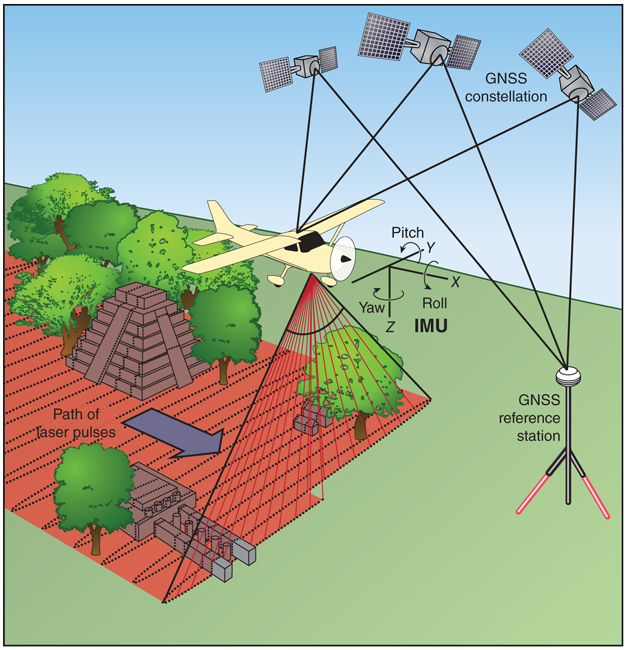
To determine coordinates for each laser return, in addition to the slant range and scanner angle at the time each pulse is transmitted, it is also necessary to know the geocentric position (X,Y,Z) and orientation (roll, pitch, and yaw) of the aircraft. This information is produced by an integrated navigation system that processes observations from global navigation satellite systems (GNSS) and from an inertial measurement unit. Once the three-dimensional positions of all the laser reflections are computed, they form what is collectively known as a point cloud. The point cloud is then analyzed by means of computer algorithms designed to determine whether the surface that produced each data point was likely to have been a human-made structure, vegetation, or the ground.
For archaeological purposes, the signals returned from vegetation are often removed from the point cloud. Those returned from the ground and from human-built structures are then used to create digital elevation models (DEMs), which are 3D grids whose coordinates represent a map of the surface beneath the forest. DEMs are a resource for professionals in several different fields—not just archaeology, but also geology, hydrology, and ecology— who use them to produce shaded relief drawings, contour maps, and other specialized types of images. Thus, airborne lidar observations can serve many purposes, with the important caveat that they provide information only on those features that have a surface signature. They cannot reveal features that are buried or those that don’t present any topographic relief or a significant difference in reflectivity from surrounding surfaces.
The new data led the archaeologists to conclude that the population of Caracol was once at least 150 percent greater than their previous estimates.
In light fixed-wing aircraft flying at low altitudes (300 to 1,000 meters above local ground level) and at relatively slow ground speeds (60 to 80 meters per second), lidar systems emitting hundreds of thousands of laser pulses per second, with electronics that can record several returns per laser pulse, have proven highly successful for archaeological mapping. Even in the dense rain forests of Central America, airborne lidar sensors have succeeded in recording sufficient reflections from the remains of ancient buildings, roadways, walls, water reservoirs, and agricultural terraces to enable analysts to create shaded relief images of the underlying terrain and structures. Those images had spatial resolutions better than one meter, typically 10 to 20 times better than the best resolutions achieved with space-based systems.
Many human-made structures can easily be recognized in the lidar data even by inexperienced viewers, either because they have regular geometric shapes, such as squares, rectangles, circles, or straight lines, or because they are themselves arranged in geometric patterns. Linear features, such as ancient roadways, walls, and irrigation canals that cut across the natural terrain, stand out particularly well. What is sometimes more difficult, even for an experienced analyst who knows the morphology of cultural and geological features of the study area, is to determine on the basis of lidar images alone whether an isolated mound is a natural feature of the terrain or the remains of an earthen pyramid. Fortunately, in such cases, the lidar observations also provide the exact coordinates of such features, thereby enabling archaeologists to navigate to them using a GNSS receiver for in-field verification.
During the past decade the National Center for Airborne Laser Mapping (NCALM), with support from the National Science Foundation, has completed more than 20 projects of archaeological interest in Mexico, Belize, Guatemala, and Honduras. The total area mapped extends over 6,500 square kilometers. Most of this work has focused on a region known to scholars as the Maya lowlands, which include the Yucatán peninsula, northern Guatemala, and Belize. The Maya culture, predominant in this region, is known for its majestic settlements composed of stepped pyramids, buildings, and temples made from masterfully cut and carved limestone. Other regions surveyed include cities of the Purépecha culture in the highlands of Michoacán Mexico, with their buildings made of volcanic rock; the masonry (raw or cut sandstone and mortar) pueblos of the Chaco culture of the American Southwest; and previously uncharted areas in the Mosquitia jungle of Honduras, where a lesser-known cultural group, most likely ancestors of the Pech, created earthen mounds that served as platforms for public buildings, temples, and homes generally constructed of wood and thatch.
In the Maya region, most of the larger ancient settlements have been known and studied by archaeologists for decades. Those easily reached from modern resort areas, such as Cancún, Puerto Morelos, Playa del Carmen, Tulum, and Cozumel, have been visited by hundreds of thousands of tourists from all over the world. Even so, the images derived from lidar point clouds have consistently shown larger extents to many of the settlements than had been recognized, along with thousands of previously unknown structures, roadways, irrigation canals, and other defensive or agricultural earthworks.

NCALM conducted the first airborne lidar survey primarily for archaeological prospection in the Maya area in 2009, covering an area of about 210 square kilometers. Centered on the Maya city of Caracol, in what is now western Belize, the survey revealed large numbers of previously unknown remains of buildings, causeways, water reservoirs, and agricultural terraces scattered well beyond the expectations of the archaeologists who had been working in the area for decades. The original survey area was enlarged by an additional 1,057 square kilometers in 2013. Arlen and Diane Chase, then at the University of Central Florida and now at the University of Nevada, Las Vegas, led the archaeology science team. They said afterward that the use of airborne lidar “has transformed our understanding of regional archaeology in the Maya area.” Indeed, the new data led the archaeologists to conclude that the population within a 100-kilometer radius of Caracol circa 650 CE might well have totaled as many as 140,000 inhabitants, a figure at least 150 percent greater than their previous estimates.

Another large-scale survey was performed by NCALM in 2015 in the Petén region of Guatemala, which encompasses about 480 square kilometers centered on the Maya city of El Ceibal. This region includes areas of protected forest, modern agricultural areas, grasslands, and both ancient and modern settlements. When the archaeologists viewed the geodetic images derived from the new airborne lidar observations, they were amazed to see previously unknown ancient ruins scattered across the entire region. A quick count identified more than 15,000 ancient structures, including pyramids, platforms, temples, walls, and urban and rural house sites.
The research team, led by Takeshi Inomata from the University of Arizona, has used lidar and excavation data to estimate that in the 480-square-kilometer area around El Ceibal, in the period between 600 CE and 950 CE, the population peaked at somewhere between 33,000 and 52,000 people. The density of the population, as measured in inhabitants per square kilometer, appears to have ranged from 780 to 1,200 at the urban center of El Ceibal and from 2.4 to 3.7 on the outskirts of the city. A surprising find among the lidar observations is the remains of what looks like a single sizable pyramid, 10 meters in height, in an area that was already familiar to the archaeologists; indeed, the site lies within an easy hike of half a kilometer or so from the side of a road that they take regularly to reach the hearth in the ceremonial center of El Ceibal.
In 2016, a survey of 2,100 square kilometers just north of El Ceibal revealed 61,480 human-built structures, a large number of them previously unknown to modern science, as well as vast areas of modified terrain that may have been used for agriculture, and extensive earthworks that were probably used either as defensive features or for water management. The survey also revealed many previously unknown large-scale settlements with ceremonial architecture. Researchers working with the Pacunam Lidar Initiative (PLI), as this project is known, estimate that between 600 CE and 850 CE, the population in the central Maya lowlands may have reached 7 million to 11 million people. The PLI archaeologists base their estimate both on the number of structures revealed by the lidar data and on the estimated amount of land that may have been used for agriculture, taking into consideration the traditional farming practices of the area, average yields, and basic caloric requirements. The estimate is somewhat conservative, falling within a range of others made for this area and time period, but the PLI team places additional confidence in it because the lidar data provides a level of detail that was not available before.
Five hundred kilometers southeast of the Maya region, a different jungle hides the ruins of a less well-known culture that has not been fully identified. Many experts believe that the inhabitants were the ancestors of a current ethnic group who identify themselves as the Pech. In 2012, NCALM carried out a survey of three areas in the remote Mosquitia region of Honduras to assist private explorers who were searching for the so-called Ciudad Blanca (“White City”) that was rumored to have existed there. In one valley alone, the lidar data revealed evidence of 19 settlements, the largest of which covered more than two square kilometers. This settlement lies along a stream and includes rectilinear mounds up to 60 meters long, 10 meters wide, and 5 meters tall, arranged in perpendicular patterns that form the shape of a plaza or city square. On-the-ground verification of the main settlements, conducted three years later, revealed that the mounds were made of compacted earth. It’s not possible to determine whether this or any other particular settlement is the legendary Ciudad Blanca, but the lidar data demonstrate that these earthen-mound settlements were widespread throughout the Mosquitia region. However, because this form of construction would have required a great deal of organization and labor for the transportation of materials, farming, and irrigation, the existence of earthen-mound settlements allows researchers to infer that the area had both significantly large populations and elaborate social-political systems.
Earthen mounds and their regular arrangement into settlements similar to those in the Honduran Mosquitia are actually widespread throughout the Western Hemisphere, from the banks of the Mississippi River in North America to the banks of the Amazon in South America. A number of ancient mounds have become relatively well known, either singly or in groups, such as Serpent Mound in Ohio, Poverty Point in Louisiana, Spiro Mounds in Oklahoma, Manitou Mounds in Ontario, Canada, and a complex of mounds in the Upano River Valley of Ecuador. However, many Americans live within a few miles of mounds that conceal the remains of ancient cities, burial grounds, and in some cases garbage dumps built by Native Americans, and assume that they are natural features of the landscape. In The Mound-Builders, published in 1930, Henry Clyde Shetrone estimated that the number of ancient human-built mounds scattered across 20 states exceeded 100,000.

The ancient city of Cahokia, built by people referred to as the Mississippians near the present-day city of St. Louis, Missouri, was once a center of business and trade rivaling the leading cities of Europe at that time. More than 120 mounds of various sizes remain today, and the area is open for viewing by the public. A stepped construction comprised of four terraces, known as Monks Mound, is the largest human-built mound that has ever been identified in the United States. Measuring approximately 300 meters in length, 200 meters in width, and 30 meters in height, this earthwork has a volume of more than 600,000 cubic meters. As attested by construction projects of this magnitude, the population of Cahokia must have been sizable at its peak: Estimates range from 6,000 to more than 40,000, with the high point coming between 1050 CE and 1150 CE, well before the arrival of Europeans in the area.
All the sites described above illustrate both how much we know and how much more we still need to learn about the geographical distribution of the people who lived in the Americas prior to the arrival of the Europeans in the 15th century. Airborne mapping lidar is a valuable tool in this process of discovery, but, as with any tool, users must keep in mind its limitations. When it comes to estimating populations on the basis of structure counts derived from lidar (or other remote sensing methods), the first and most obvious limitation is that much of the evidence of early settlements has already been destroyed by modern settlements and infrastructure; thus, there is a risk of underestimating the former populations. In areas where forests have stopped the clock and ancient settlements may seem to be frozen as they were at the time of their abandonment, lidar may be able to pick up only the remains of the larger ceremonial or governmental structures. However, smaller structures, such as the foundations of small residential buildings, may now be unrecognizable because they are buried by sediment or because they have suffered from erosion and weathering over the centuries. But a larger problem is that the structures that can be detected by archaeologists in lidar data or through field surveys may not have all been occupied at the same time, and researchers must allow for this possibility in order to avoid overestimates. Determining which structures were being used at a given time is a long and tedious process that requires traditional archaeological fieldwork such as the excavation, recovery, and dating of stone carvings, pottery, construction materials, and perhaps even the remains of the humans who once lived there. Archaeological science, like any other science, is constantly refining its practices and state of knowledge. Therefore, archaeologists have been refining the multiple factors and considerations that go into deriving these population estimates so as to avoid overestimation and underestimation. Constantly, the archaeological community conducts studies aimed at refining values for factors such as the probable number of persons that inhabited or could be associated with different types of structures, the number of structures that remain hidden in proportion to those that we are able to detect with lidar or by other means, the ratio of structures that are occupied to those that are unoccupied for a given time period, and so forth.
What the archaeological community has learned in a new era of exploration using airborne lidar in Mexico and Central America is that unknown settlements are being identified in almost every area mapped, and that the sites that were previously known are now proving to be larger and more complex than originally thought. Likewise, the investments made in infrastructure for agriculture, water management, transportation, and defense are larger than previously identified or imagined. All these new insights are leading to revised hypotheses not only about population values but also on agricultural and land modification practices, trade, warfare, political control, and social interaction.
Given that there are still vast tracts of land covered by jungle about which little is known of the inhabitants prior to the arrival of European explorers—the Mosquitia in Honduras and Nicaragua, the Darien in Panama and northern Colombia, and the high cloud forest of the Andes, and the largest tropical forest of all, the Amazon, to name just a few—it is not difficult to imagine that lidar may reveal new evidence of large ancient settlements, which will continually and dramatically increase the population estimates of pre-contact America.
The major efforts the archaeological community has expended so far, employing lidar to map archeological areas in Mexico and upper Central America, have revealed less than 5 percent of the area covered by dense forest in that region. Mapping the remaining 95 percent may seem like an impossible challenge. Fortunately, however, newer airborne lidar technologies now available could complete that task in perhaps a decade or so if sufficient financial support were available. A greater challenge would be the raising of an army of archaeologists ready to analyze, interpret, and field-validate all the remotely collected data. We hope the resources will be found to expeditiously collect the necessary airborne lidar observations and produce the bare-earth images that will enable archaeologists to reduce the uncertainties in estimates of the pre- Columbian population, to the point that there will no longer be high counters and low counters in our community. Even if that feat proves impossible, the use of airborne lidar observations is certain to result in fascinating discoveries about the people who inhabited the Western Hemisphere centuries before the arrival of Europeans.
- Canuto, M. A., et al. 2018. Ancient lowland Maya complexity as revealed by airborne laser scanning of northern Guatemala. Science 361:1313–1314.
- Carter, W. E., R. L. Shrestha, and J. C. Fernandez-Diaz. 2016. Archaeology from the air. American Scientist 104:28–35.
- Chase, A. F., D. Z. Chase, J. J. Awe, and J. F. Weishampel. 2014. The use of LiDAR in understanding the ancient Maya landscape. Advances in Archaeological Practice 2(3):208–221.
- Chase, A. F., D. Z. Chase, and J. F. Weishampel. 2010. Lasers in the jungle. Archaeology 63(4):27–29.
- Fisher, C. T., A. S. Cohen, J. C. Fernandez-Diaz, and S. J. Leisz. 2017. The application of airborne mapping LiDAR for the documentation of ancient cities and regions in tropical regions. Quaternary International 448 (suppl. C):129–138.
- Inomata, T., et al. 2018. Archaeological application of airborne LiDAR to examine social changes in the Ceibal region of the Maya lowlands. PLoS One 13(2):e0191619.
- Mann, C. 2011. 1491: New Revelations of the Americas Before Columbus. New York: Vantage Books.













American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.