The Curse of E=mc2
By Tony Rothman
The most famous equation has a history that goes far beyond Albert Einstein, and a meaning that is far less straightforward than is commonly believed.
The most famous equation has a history that goes far beyond Albert Einstein, and a meaning that is far less straightforward than is commonly believed.

Hollywood stars, one imagines, receive at breakfast each morning cartons overflowing with letters from adoring fans—or, more likely these days, collections of emails, Facebook posts, and Instagram comments—sorted by personal assistants into relevant categories: “gushing praise”; “everlasting devotion”; “marriage proposals”; and “autographed photo request (price list sent).”
Physicists occasionally get mail, too. The most popular topics are “Einstein was wrong”; “Einstein was a fraud”; “Attached find my unified field theory correcting Einstein.” Sometimes UPS delivers the proposals as entire crates of self-published books on why relativity is incorrect. Those of us who receive such submissions tend to file them under “Prophets and Cosmic Visionaries” or “Delete,” or we may silently excuse ourselves by forwarding the submissions of one author to another, and vice versa, allowing them to debate matters intelligently among themselves. Letters from prophets invariably conclude with, “I expect your positive evaluation within three days.”
Einstein’s defenders are as zealous as his deniers. The smallest publication by a physicist that touches upon relativity invariably elicits responses of the form, “You claim Einstein made a mistake. In fact, Einstein was anointed by God, and you are an idiot.” It is sometimes the case that such letters are signed by colleagues.
To the public, if not to scientists themselves, the focal point of Einstein fixation is E=mc2. No other equation in the history of the world has a more compact and ironclad biography or a more succinct meaning: In 1905, several months after completing his special theory of relativity, Albert Einstein perceived that mass and energy were equivalent and proved that the energy content of any body is equal to its mass times the speed of light squared, E=mc2. Thus the story of the equation has come to symbolize Einstein’s entire body of work, if not all of modern physics, and has firmly embedded itself into pop culture.
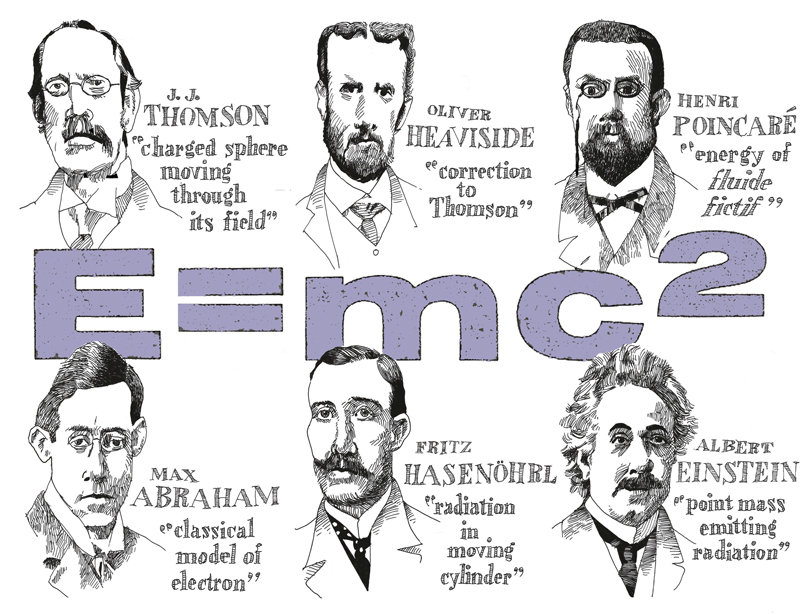
Illustration by Tom Dunne.
But as is generally the case with isolated-genius science stories, this one is a fairy tale, or at least it veers strongly in that direction. Einstein was not the first physicist to suggest that energy behaves as if it possesses mass, and if he was indeed the first to write down the correct general expression, a professor grading the 1905 paper in which he gave his derivation of the mass–energy relationship would deduct points for unjustified and incorrect assumptions. Indeed, Einstein wrote half a dozen further papers to patch up his argument, never succeeding. Debate continues today over the proper approach to establishing the relationship, over whether relativity is necessary, and even over whether the equation is correct in all circumstances.
The mail being inexorable, a physicist well knows what he is in for if he ignores Will Rogers’s immortal adage, “Anyone who speaks aloud of E=mc2 is a blockhead.” But let us go ahead and be a fool, or a blockhead, and outline the history and conflicts surrounding E=mc2, attempting to steer between extremists on the left and the right. Bear in mind that, mathematical proofs notwithstanding, physics is ultimately an experimental science and the correctness of any proposal is decided by trial and error. E=mc2 is by now used daily in situations ranging from subatomic physics to bomb simulations to black hole accretion disks, and no one seriously doubts that it will endure forever as one of the foundations of our description of nature.
With the advent of James Clerk Maxwell’s theory of electromagnetism in the 1860s, natural philosophers were faced with two towering, competing worldviews: Newtonian mechanics, which had dominated scientific thinking for two centuries, and the Scottish physicist’s nascent theory. The former interpreted nature in terms of particles and forces. The latter described the behavior of waves and fields, in particular electromagnetic fields that propagated as light waves. Which was the more fundamental?
The answer was not obvious. Maxwell himself had developed electromagnetism with analogies to Newtonian hydrodynamics. He imagined space to be filled with fluids that contained vortices and elastic stresses that transmitted radiation from one place to another. His successors pushed such analogies to extremes, enlisting vortex springs and even vortex sponges embedded into seemingly empty space to explain wave propagation. From that viewpoint, Newtonian mechanics was surely the more fundamental theory. On the other hand, a philosopher who viewed the world as composed of charged particles each carrying its own electric and magnetic fields might well regard electromagnetism as the basis of nature.
There was a widespread idea that mass was a property “induced” by the interaction of charges and fields.
Toward the close of the 19th century, probably more physicists were Maxwellians than Newtonians. As Austrian physicist Ludwig Boltzmann remarked in 1897, “The advantage of deriving the whole science of mechanics from conceptions, which anyhow are indispensable for the explanation of electromagnetism, would be as important as if conversely electromagnetic phenomena were explained on the basis of mechanics. May the former succeed.”
A cornerstone of the belief that all mechanical phenomena could be reduced to electromagnetism was the idea that mass itself was a property “induced” by the interaction of charges and fields. The first attempt to demonstrate that claim was made in 1881 by a 25-year-old J. J. Thomson, the British physicist who later achieved renown as one of the discoverers of the electron.
Thomson reasoned along the following lines. When you drop an inflatable beach ball to the sand, you see that it falls much more slowly than it would were gravity the only culprit at work. You might think that the drag produced by the air on the ball accounts for the discrepancy, but this is far from the whole story. Even if the ball were perfectly smooth, with zero drag, it would still have to push the air ahead of it out of the way. The mass of that air must somehow figure in the ball’s inhibited motion.
How much air is being pushed? It turns out that for air flowing without turbulence around a perfectly smooth ball, you have to add exactly one-half the mass of the displaced air to the mass of the ball. You can imagine the beach ball pushing a virtual ball ahead of it whose mass is one-half the mass of the air contained in the real ball. Because the drag on the ball itself is zero, the slowed falling of the ball must be a purely inertial effect: Due to its motion, the ball behaves as if its mass has increased, and hence its acceleration has decreased. The effect of this additional, or induced mass becomes significant when the density of the surrounding fluid is comparable to the density of the accelerating object. For example, the density of water is comparable to the overall density of a ship, and the water must be pushed out of the way as the ship plows forth, so nautical engineers are well aware of the induced-mass phenomenon.
By analogy, Thomson imagined a charged sphere moving through space. Because the sphere is charged, it carries an electric field, and because it is moving, it generates a magnetic field. Thomson argued that this self-generated magnetic field must impede the charge’s motion just as the air impedes a falling ball. If it accelerated the charge, the charge’s energy and velocity would increase, further increasing the magnetic field, further accelerating the charge . . . ad infinitum. Perpetual motion machines are forbidden in physics, so the magnetic field must act to decelerate the charge. Because there is no friction in this system, the sphere must slow down as if its mass were increasing, like the beach ball moving through the air. Thomson’s calculations showed that the sphere’s mass should increase by what amounted to (8/15)E/c2, where E represents the electric field energy. For Earth, Thomson estimated the induced mass to be “about 650 tons . . . quite insignificant when compared with the mass of the earth.”
Couched as it was in slightly hypothetical language, it’s not entirely clear how seriously Thomson took his result, but the multifaceted English physicist and electrical engineer Oliver Heaviside certainly did. Heaviside apparently believed that induced mass was a genuine physical phenomenon, writing in an 1889 paper of the “electric force of inertia.” His version of Thomson’s calculation gave for the sphere's mass (4/3)E/c2 [see box below]. If one accepts the line of reasoning, then Thomson and Heaviside had established by then that mass can be associated with the energy of the electromagnetic field.
Any account of the early history of relativity inevitably runs into the universal French mathematician, engineer, physicist, and philosopher Henri Poincaré, who in particular contributed penetrating thoughts concerning the inertia of energy. Since Newton’s day, physicists had asserted that nature obeys conservation of momentum. In other words, an isolated system’s total momentum (the sum of all the particle masses multiplied by their velocities) always remains constant. Energy, of course, is also conserved for material systems, and in 1884 John H. Poynting extended this idea with a famous theorem that expressed the law of energy conservation for the electromagnetic field. Poincaré realized that Poynting’s theorem had an important implication: that the electromagnetic field also carries momentum.
In 1900, Poincaré published a paper in which he proposed that the field and particle momenta should be conserved together, which was problematic, because the momentum of particles was happily conserved on its own. Nevertheless, by enlisting Poynting’s theorem, Poincaré could achieve his goal of a unified conservation law if he regarded electromagnetic energy as a fluid traveling through space with a density such that E=mc2. That did the trick, as long as the electromagnetic energy density remained constant. As there was no obvious reason for this to be the case, he regarded his analogy as a fluide fictif (fictious fluid), a mathematical construct allowing the system’s total momentum to be conserved.
Nevertheless, in broadening the realm of momentum conservation, Poincaré’s proposal represented a significant conceptual advance, one that his German colleague Max Abraham pushed further in his theory of the classical electron. His calculation of the electron’s mass, due to the particle’s interaction with its own electric field, again gave (4/3)E/c2 [see box below]. The persistence of the 4/3 factor, which looks decidedly weird to modern eyes, is made inestimably odder by the fact that it refuses to go away under straightforward relativistic calculations. The correct way of disposing of it is debated even today, but for the moment we gently tiptoe around the notorious 4/3 problem.
A substantially different approach to the relationship between mass and energy was taken by Fritz Hasenöhrl. Largely forgotten today, Hasenöhrl was considered one of the leading physicists in Austria of the early 20th century. Born in 1874, he studied physics under two luminaries, Franz Exner and Ludwig Boltzmann, at the University of Vienna. In 1907, after Boltzmann committed suicide, Hasenöhrl succeeded his teacher as professor of physics and soon counted quantum physics pioneer Erwin Schrödinger among his students.
In 1904, Hasenöhrl made what was to become the most publicized pre-Einsteinian attempt to establish the equivalence of mass and energy—perhaps too publicized. Years later, the physicist and virulent anti-Semite Philipp Lenard, who became Hitler’s Chief of Aryan Physics, attempted to discredit Einstein by awarding the discovery of E=mc2 to Hasenöhrl. Since then, crackpots and anti-Semites of the world have latched on to Hasenöhrl, adding their conspiracy theories to physicists’ mailboxes.
Einstein did not prove that all forms of energy possess mass, nor did he explain how mass–energy conversion comes about.
Nevertheless, credit is due the man. In a trilogy of papers published under the collective title “On the Theory of Radiation in Moving Bodies,” the final two of which appeared in Annalen der Physik in 1904 and early 1905, Hasenöhrl asked whether heat energy—blackbody radiation to physicists—emitted by the endcaps inside a moving, cylindrical cavity manifests inertia. He answered his question in the affirmative, stating that blackbody radiation has “an apparent mass equal to (8/3)E/c2,” which in his final paper he corrected to (4/3)E/c2 [see box below]. The similarity of his result to Abraham’s is not surprising, given that the underlying physics in both analyses is Maxwell’s theory. However, Abraham was considering an electron, whereas Hasenöhrl was considering heat radiation contained in a moving cylinder. In the former, the relevant energy is that of the electron’s field; in the latter, it is the thermal energy of the heat.
It should be emphasized that Hasenöhrl was working from a Newtonian worldview, in which scientists imagined that light could travel at varying speeds through the universal medium of the light-bearing ether, and that different clocks always measured the same time when their springs were functioning. Moreover, the cylinders of Hasenöhrl’s thought experiments are macroscopic objects, making the problem far more difficult than those involving idealized point masses. And although Hasenöhrl’s first experiment was modeled on a cavity moving at constant velocity, he made his own life infinitely more miserable by next considering cavities undergoing acceleration, for which he also found m=(4/3)E/c2. Despite the handicaps, Max Planck and Wolfgang Pauli—two other leading figures in the development of quantum physics—acknowledged Hasenöhrl as the first to point out that blackbody radiation possesses inertia.
With Hasenöhrl’s publications, the stage was set for Albert Einstein. Compared to his colleague’s trilogy, Einstein’s paper, “Does the Inertia of a Body Depend on Its Energy Content?” received by Annalen der Physik in September 1905, is a masterwork of simplicity, only three pages long. After summarizing his new theory of relativity, in which the speed of light is constant, Einstein wisely considers the simplified case of the classic introductory physics mass: a block. He imagines that the block, sitting contentedly at rest, suddenly emits two equal bursts of light in opposite directions. He then assumes that the block’s mass must decrease after this emission of radiation. The question is, how much?
Einstein answers by asking how the situation appears to an observer who is moving at some velocity v with respect to the block. To that observer, it is the block that is moving—at the same speed but in the opposite direction. Before the burst of radiation, the moving block has an energy of motion, kinetic energy, given by the standard formula (1/2)mv2. After the bursts of radiation, this energy must change [see box below]. Einstein equates the change in kinetic energy to his recently derived formula for the energy E inherent in a beam of light. In a few short lines, he reaches the conclusion now chiseled in eternity, E=Δmc2, where Δm represents the change in mass.
However, in 1905, Einstein did not know the relativistically correct expression for kinetic energy, which was proposed by Polish-German mathematician Hermann Minkowski only in 1908. Einstein thus resorted to the Newtonian equation for kinetic energy, essentially approximating away the relativistic bits of his calculation to arrive at an answer that is attainable using Newton’s and Maxwell’s physics. Arguably, the quintessential equation of relativity contains no relativity. And by the way, E=mc2 never appears in the paper. Einstein writes, “If a body gives off the energy L in the form of radiation, its mass diminishes by L/c2.” He didn’t write the equation in its famous form until his 1912 “Manuscript on Special Relativity.”
On the one hand, Einstein’s conception of mass–energy equivalence was a definite conceptual leap from the Maxwellians: No longer was mass tied to a charge’s motion through an electromagnetic field. On the other hand, contrary to popular belief, Einstein did not prove that all forms of energy possess mass. That’s what he conjectured at the close of his paper. In his calculation, mass is converted specifically into light (electromagnetic radiation), which is only one form of energy. As heat is also a form of electromagnetic radiation, in that respect it is not obvious that Einstein’s result was more general than Hasenöhrl’s. Moreover, Einstein never explains how mass–energy conversion comes about; if it cannot take place, then the famous result holds no content. Nevertheless, the conjecture that mass should change under emission of any sort of energy was probably Einstein’s greatest contribution to the problem. Neither the Maxwellians nor Hasenöhrl had considered such a possibility.
Einstein was well aware of the deficiencies of his proof of mass–energy equivalence, and over the next 40 years he wrote six further papers attempting to correct it. Physicist Hans Ohanian at the University of Vermont persuasively argues that they all contain errors. It was not until 1911 that German physicist Max von Laue, using mathematical methods unfamiliar to Einstein in 1905, showed that if E=mc2 holds for an idealized point mass, such as a basic physics block, then it also holds for an extended, static system as long as the system is “closed,” meaning that no external forces act upon it. In 1918, German mathematician Felix Klein extended Laue’s result to systems that weren’t static but changed with time. With the Laue–Klein theorem, most physicists came to accept that E=mc2 had been satisfactorily established, at least theoretically.
Inevitably one wonders whether Einstein knew about Hasenöhrl’s work. Lacking a time machine, we cannot definitively answer this question. Without ever explicitly mentioning Hasenöhrl, Einstein always insisted on his priority regarding the discovery of mass–energy equivalence. Still, it is hard to believe he was unaware of a series of award-winning papers published by a prominent colleague in the leading German physics journal, to which he himself had been contributing since 1901. It seems likely that Einstein saw Hasenöhrl’s papers and they inspired him to do better; the similarity of their thought experiments only strengthens that suspicion.
At some point, Einstein certainly became aware of Hasenöhrl, as evidenced by a famous photo of the first Solvay Conference, held in Brussels in 1911. There seem to have been no hard feelings, at least on Hasenöhrl’s part. According to Hasenöhrl’s student Hans Thirring, after the debut of special relativity, Hasenöhrl became one of its first exponents. Tragically, Hasenöhrl never got to tell his side of the story. At the outbreak of World War I, he enlisted in the Austro-Hungarian army and was killed during the Isonzo campaign in what is now Slovenia, in 1915.
While the Laue–Klein theorem put E=mc2 on a firmer theoretical footing, experiments involving the particles and energies released during the radioactive decay of atomic nuclei were starting to lend empirical confirmation to Einstein’s prediction. James Chadwick’s 1932 discovery of the neutron, whose mass was consistent with that predicted by E=mc2, was a significant signpost along this road. Within a few more years, mass–energy equivalence became regarded as an experimentally confirmed law of nature. But it was undoubtedly the atomic bomb, whose enormous destructive power is a direct result of the conversion of mass into energy, which welded Einstein’s name to E=mc2 once and for all.
Yet our tale is hardly done. You have undoubtedly been wondering where Hasenöhrl went wrong, and how to get rid of the damned 4/3 that figures in his cylinders and Abraham’s electrons. Insofar as quantum field theory—a framework for understanding the interaction of light and elementary particles—was developed largely to deal with the pathologies inherent in Abraham’s model of the electron, the problem actually becomes central to 20th-century physics. You may have also been wondering why Abraham’s electron doesn’t fly apart under the mutual repulsion of its negatively charged parts. Poincaré wondered the same thing, and suggested that the tiny ball could be glued together by elastic forces, which oppose the pressure arising from the electrical repulsion.

Photograph by Benjamin Couprie, 1911 / Wikimedia Commons
Hasenöhrl’s thought experiments manifest a similar dilemma. Hasenöhrl imagined his radiation to be confined in a cylinder, which must manifest stresses to counteract the radiation’s pressure, just as the elastic stresses in a balloon confine the air inside. Such stresses possess energy, and if one accounts for that energy properly using the Laue–Klein theorem (which deals with extended systems), the result should come out to a clean E=mc2. At least, that is, according to physics folklore, which turns out to be . . . folklore. Laue and Klein had assumed that no external forces act on the system, but Hasenöhrl explicitly enlisted external forces to hold the endcaps of his cylinder in position, like the fingers of God, and therefore the Laue–Klein theorem is not applicable.
What, then, explains the 4/3 factor? Because the endcaps in Hasenöhrl’s cylinder are radiating heat, they must be losing mass—something that Hasenöhrl failed to realize. He calculated only the apparent mass inherent in a parcel of radiation, never considering the conversion of mass into energy. If you take the mass loss into account, you do get a result consistent with relativity. Success? Not so fast. Believe it or not, you still apparently get m=(4/3)E/c2. But once again, Hasenöhrl’s cylinders do not represent a closed system, and so it is not a foregone conclusion that the final result must be E=mc2. If Einstein could have performed a complete relativistic analysis in 1905, he would have had to concede that Hasenöhrl’s result was compatible with his new theory of special relativity.

Image (left) from HathiTrust Digital Library. Photograph (right) by Lynne Sladky / Associated Press / AP Images
Einstein would, but Enrico Fermi wouldn’t. Indeed, the Italian physicist would reject everything just said as complete nonsense. In one of his earliest papers, Fermi attempted to eliminate the vexing 4/3 from Abraham’s electron and, with his colleague Aldo Pontremoli, subsequently applied the procedure to Hasenöhrl’s cavity as well. Fermi’s point was, firstly, that Poincaré’s stresses, designed to glue the electron together, are entirely fictitious, invented merely to solve the problem. Secondly, Fermi understood that time may be universal in Newton’s world, but in Einstein’s world it is not. If, to someone riding astride Hasenöhrl’s cavity, two forces are applied at the same time to the cylinder ends, then relativity implies that someone who sees the cavity moving also sees the forces applied at different instants. During the interval between those moments, the velocity or radiation pressure, for example, may have changed. Therefore, the two observers are essentially describing two different physical systems. The Laue–Klein theorem cannot provide the proper basis for resolving the paradox, because it adds up all the energy contributions across the cylinder at a single instant of time, and the contributions at that instant don’t correspond to those in another observer’s reference frame.
By correctly transforming the times between reference frames, Fermi and Pontremoli claimed to rid the world of 4/3 and restore E=mc2. Unfortunately, even in those days authors apparently cited papers they hadn’t read. Their solution required that the system be accelerating, which was simply not the case in Hasenöhrl’s initial thought experiment. Furthermore, to make the difficult problem of accelerating extended systems tractable, Fermi and Pontremoli (like Hasenöhrl) made simplifying assumptions, in particular that the system is accelerating slowly. Not all objects are accelerating slowly, however, so their proofs are hardly universal. What’s more, the Italians left completely unexplained why the electron doesn’t fly apart, consigning the resolution of that problem to quantum field theory, in which the electron is merely assumed to be stable.
Thus swords clang into the sunset. Yes, it’s true: To this day, there is no universally accepted resolution to the 4/3 problem, and when it’s not completely forgotten, papers debating the subject now and again continue to appear in technical journals. Members of Fermi’s corps attack the Poincaré-Laue-Klein camp because their methods seem to violate the spirit and letter of relativity. The Poincaré-Lauists counterattack by pointing out that Fermi-ists simply do not explain why Abraham’s electron is stable, or that while performing relativistic transformations between reference frames, they pay no attention to how a cavity physically confines the radiation inside it.
The vituperative exchanges amply confirm the sage warning to those who dare speak of E=mc2. One reason why the 4/3 problem triggers such intense emotions is that it touches not only on the foundations of physics, but also on what all physicists think they understand in the marrow of their bones. When someone proposes an amendment to that understanding, the first reaction is that whoever has suggested it must be a fool or a buffoon. What’s more, the mathematics of special relativity may be well suited to idealized blocks traveling at constant velocity, but it is not as well suited to problems involving extended objects and accelerations, where 4/3 rears its head. As a result, considerable effort is required to attach a physical picture to the equations, which are always smarter than we are.

Ace Magazines
The moral is that history is richer than its sound bites and the theory of relativity is richer than its classroom reductions. It is much more complicated, certainly, than relativity extremists seem to believe. Focusing on icons may shine a spotlight on one scientific superstar or one notable equation, but tracing the development of an idea illuminates a far more satisfying landscape—one that inspires participation rather than worship, and one that perhaps even sparks a new thought or two of your own. As commonly taught today, relativity is a world of a few basic equations applied to pat scenarios. It is a world where, simply and obviously, E=mc2. But the early years of relativity were an unfamiliar borderland where accelerating cylinders and spinning wheels stretched intuition, leading to paradoxes that forced physicists to ask even whether special relativity was the best theory to handle such conundrums.
Today’s physicists would do well, from time to time, to go back to basics and walk the same terrain as relativity’s early investigators. There they would soon encounter a famous puzzle only slightly less perplexing than the 4/3 problem. According to the basic precepts of relativity, someone watching a spinning wheel will see its circumference shrink, but not its radial spokes. If the wheel is perfectly rigid, then, it must snap, no? Is there such a thing as a perfectly rigid object in special relativity? Or, if the circumference of the wheel has shrunk, does that mean that the ratio of the circumference to the diameter of a circle is no longer π? In that case, have we crossed from the territory of special relativity to Einstein’s theory of gravity, general relativity, whose province is non-Euclidean geometry? Do accelerating cylinders and spinning wheels produce artificial gravity, or in fact have they produced the real thing? With respect to what is the cylinder accelerating?
These should be legitimate questions to ponder in academic offices, not just in random letters. In filing away problems such as Hasenöhrl’s cylinder as quaint artifacts, or forgetting them entirely, both history and physics have become the poorer.
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.