American Scientist

The British philosopher Bertrand Russell once said that "it must have required many ages to discover that a brace of pheasants and a couple of days were both instances of the number two." That discovery, however, was made not by the brace of pheasants, but the philosopher himself, presumably as an adult human being. And what of the pheasants? Are they capable of understanding that as a pair they represent the number two?

Birding wisdom holds that to watch most birds without disturbing them, it is best to hide behind a blind. If the bird sees you enter, however, you're not much better off because it is now aware of the blind. One way around this problem is for two people to enter the blind together. Some time later, one person leaves and the bird, apparently assuming the coast is clear, goes back to business as usual. Why? Because most birds observed in this situation are incapable of computing a simple subtraction: 2 - 1 = 1!

It would seem that, if birds are any indication, animals are far from the most astute of mathematicians. But we do know that animals must have at least limited numerical capabilities. Species with widely different life cycles, ecologies and mating systems have been known to engage in varied forms of mental calculus designed to maximize energetic intake: They calculate average rates of return in food patches, use information about search costs and search speed to assess optimal rates of return, obey Bayes's theorem (a calculation of the probability of future returns based on prior experience) and hide seeds over a broad swath of turf, returning months later to retrieve their stash. These calculations show that animals are indeed equipped with some form of powerful "number-crunching" device.

When facing competition within and between groups, social animals often adhere to the dictum "there is strength in numbers." In chimpanzees, for example, attacking and killing a member of another community occurs only if the intruder is alone and there are at least three adult males in the attacking party. Within social groups, individuals may form coalitions of two or more members to increase their relative dominance over a third individual. In bottlenose dolphins, such coalitions can reach exceptional levels of sophistication. Two to three males in one coalition join up with a second coalition to defeat a third. Occasionally, a large group of 14 male dolphins forms a team that readily overpowers smaller groups. And for what? A single, sexually receptive female. It remains to be seen, however, whether a group's superiority arises from overall numerical superiority or from some other, as yet undiscovered factor. For example, what if the total number of individuals in the two united coalitions is four and the number of individuals in the single coalition is five? Here, two coalitions are greater than one, but five is greater than four. If dolphins are truly counting the number of individuals, then such differences matter.

It is clear that animals have need for certain basic arithmetic calculations. We know little, however, about how they represent those calculations, and the corresponding numbers, in their heads. There are two popular experimental designs from which we hope to gain insight into the conceptual representation of numbers in both animals and people: those that explore spontaneous representations of number and those that involve training.

Magic with Numbers

One recent approach to understanding animal cognition takes advantage of a technique originally developed for human infants. Called the expectancy-violation technique, it uses the twisted logic of a magic show to explore spontaneous representation in animals. Here's the basic principle: Imagine a magic show in which the magician walks on stage, saws a human body in half, separates the pieces and, with a wave of the wand, brings them together again. The victim sits up, perfectly aligned and good as new. The audience stares in amazement. Why? Because adult humans know that the magician has violated a fundamental physical principle: Human bodies can't be sawed in half and then brought back together again. But would human infants watching the same show be equally amazed? Do they respond differently to "magical" deviations of physical principles than to events consistent with those principles? If so, the logic goes, then they have detected a violation and have expressed some level of understanding of physical principles.

Developmental psychologist Karen Wynn of Yale University used the expectancy-violation technique to explore whether five-month-old human infants can compute simple math problems, such as 1 + 1= 2. To remove the effects of novelty, the experimenter must first familiarize the infant with the key objects and non-magic events. In this particular study, the experimenter showed an infant either one, two or three Mickey Mouse dolls on a stage, as well as a screen that moved up and down. Test trials started once the infant was bored, looking away from the stage. In the "expected" test (1 + 1 = 2), an infant watched as an experimenter lowered one Mickey Mouse doll onto an empty stage. A screen was then placed in front of the doll. The experimenter then produced a second Mickey Mouse doll and placed it behind the screen. When the screen was removed, the infant saw the expected outcome: two Mickeys on the stage. No magic.

In the "unexpected" test, the infant watched the same sequence of actions, involving the same two Mickey Mouse dolls but with one crucial change—a bit of backstage magic. When the experimenter removed the screen, the infant saw either one doll (1 + 1 = 1) or three (1 + 1 = 3). Wynn found that five-month olds consistently look longer (about two seconds more) when the outcome is one or three Mickeys than when the outcome is two. And precisely the same kind of result emerges from an experiment involving subtraction (2 - 1 = 1) instead of addition.

Wynn concluded that infants have an innate capacity to do simple arithmetic. By simple, she meant addition and subtraction with a small number of objects. By innate, she meant that the general capacity to track objects and perform arithmetical operations on them comes standard as part of our genetic equipment.

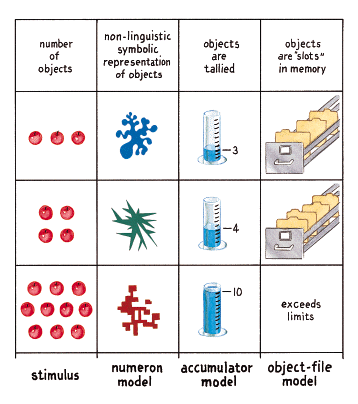
Wynn's results raise fundamental questions about the development and evolution of nonlinguistic representations. For example, what kind of representation does an infant have while watching Mickey Mouse dolls come and go? Do infants have access to nonlinguistic mental symbols—what cognitive scientists Randy Gallistel and Rochel Gelman at the University of California, Los Angeles call "numerons"—that allow them to tag individual objects as they appear and then disappear behind the screen? When an infant sees one doll, does some kind of nonlinguistic symbol light up in her brain? When a second doll is introduced, does a different symbol, one representing the number two, light up? Or maybe infants lack such symbols altogether. Perhaps they assess number by storing information about each object in their memory banks, folders within the brain's "filing cabinets" that can later be retrieved and processed. Alternatively, they might compute number by means of an internal metronome that tallies the number of objects perceived. As each object is registered, a record might accumulate, much the way mercury registers changes in temperature or sand fills a graduated cylinder. These are all possible mechanisms by which number representation might occur in human infants. And, as several experiments now show, they are possible mechanisms for non-human animals as well.

One, Two, Three, Many?

Working with some of my students, I set up a magic show for the rhesus monkeys living on the Puerto Rican island of Cayo Santiago. More than 1,000 monkeys live wild on the island; on encountering a solitary curious individual, we set up to begin a trial. We started with a virtually identical version of Wynn's 1 + 1 = 2 task for human infants. Rather than Mickey Mouse dolls, however, we used bright purple eggplants. After familiarization to the eggplants and display box, the rhesus were presented with a series of test trials. In each trial, the subject watched as an experimenter placed two eggplants behind a screen and then removed the screen. Just as the human infants had done, the rhesus tended to look longer when the test outcome was one or three eggplants than when it was the expected two. Rhesus monkeys appear to understand that 1 + 1 = 2. They also seem to understand that 2 + 1 = 3, 2 - 1 = 1, and 3 - 1 = 2—but fail, however, to understand that 2 + 2 = 4.

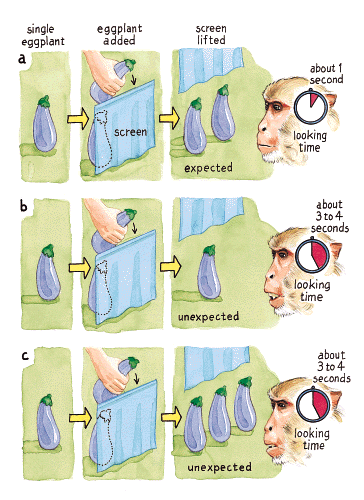
Based on studies using the expectancy-violation procedure, the limit for spontaneous number discrimination in human infants and rhesus monkeys is approximately three. Given their ability to visually discriminate small numerosities, I then asked the question, along with developmental psychologist Susan Carey and my veterinarian wife, Lilan Basse Hauser, whether infants and monkeys are capable of acting on this knowledge. We have recently completed a set of experiments on rhesus monkeys that builds on the logic of the earlier eggplant tests but requires active searching rather than mere looking.

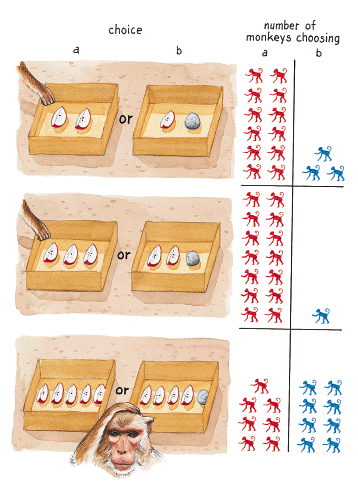
Attempting to simulate a natural foraging experiment, we offered the rhesus a choice between two food quantities. In the experiment, the monkey sat and watched as an experimenter put several pieces of apple into one box, followed by several pieces of apple into a second box. Initially, one box always received one more piece of apple than the other. As soon as both boxes were loaded with apple slices, the experimenter walked away and allowed the subject to approach. The rhesus monkeys consistently selected the box with the larger quantity of apple slices, discriminating quantities up to four versus three pieces. At five versus four pieces, however, the monkeys failed to show any systematic preference, sometimes selecting the box with five apple slices and sometimes the one with four. When the interval was increased to five versus three, the monkeys consistently selected five.

These results suggest that rhesus monkeys have a system of spontaneous quantification that translates to something like one, two, three and many. It must be remembered, however, that these experiments may be confounded by time. Simply, it takes longer to place four slices of apple into the box than it does to place three. Thus, the rhesus monkey could pick the box with more food based on the time it takes to place apple slices into the box rather than the actual number of slices. To eliminate this complicating factor, we reran the experiments controlling for time: We placed three apple slices in one box versus two apple slices and a rock in the second box. Although both the number of objects and the time required to place objects into each box were equated in the two boxes, the subjects continued consistently to select the box with more apple slices. And, as in the first condition, their ability to select the box with the larger amount of food was limited to a discrimination between four and three slices.

Studies of rhesus-monkey foraging decisions indicate that animals spontaneously, and without training, exhibit rudimentary numerical abilities. From a comparative perspective, the limit on spontaneous number estimation in rhesus monkeys based on looking and foraging is interesting because it parallels the limits of human infants. It also corresponds to the range in the syntax of natural language: Human languages tend to have words for one, two and three and use an expression such as many to denote entities greater than three. Such convergence suggests that the brain mechanism underlying spontaneous numerical estimation is shared across a diversity of animals. This hypothesis raises several crucial questions: First, are there conditions under which more sophisticated numerical capacities can be elicited in animals? And what social or ecological pressures would favor a mind capable of more precise numerical quantification? The answer to the first question is "yes," but in order to fully comprehend how and why, we must consider the second category of experimental approaches, those that involve extensive training.

In an example of a typical animal-learning experiment, rats or pigeons are placed in a Skinner box—a cage with a few lights, a food dish, several buttons and a system of wire relays—and set on a schedule of reinforcement in which every press or peck on a button yields one food pellet. With proper training, rats and pigeons easily learn this task. Now change the reinforcement schedule: For every three presses, one food pellet is delivered. The animals quickly adapt. They are even capable of grasping that to retrieve one pellet, they must press 24 times, no more, no less. Even more astonishing is this: Place a pigeon in a Skinner box with three buttons, the left of which provides food if pecked 45 times, the right if pressed 50 times. When the center button lights up, the pigeon pecks away until the experimenter turns the light off, after either 45 or 50 pecks. Next, both side buttons are illuminated. The pigeon must recall how many times it pecked before the experimenter turned the light off, and then peck the side button associated with this number. Thus, if the pigeon pecked 45 times on the center button, it must turn and peck the left button. Incredibly, pigeons solve this problem.

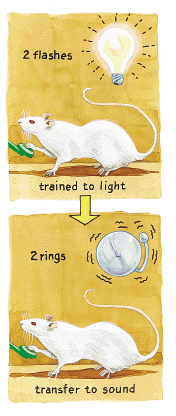
There's more. Teach rats to press one button when they see two light flashes and another button for four light flashes. No problem. Now, present either two or four sound beeps in succession. The rats immediately transfer their knowledge from the visual to the auditory modality and do so even when the duration of the flashes or tones varies. All that seems to matter is the number of cues. In this study and many others, researchers have systematically varied the length of time a cue is presented, how hard it is to depress the lever, the amount of time elapsed between presentations and the subject's hunger level. All of these factors could serve as cues for figuring out when to press and how often. Rats and pigeons nevertheless ignore these cues, using only the number of presses to maximize the amount of food obtained.

Numbers: Category vs. Concept

It is clear that animals have a number category, which, like the categories solid object and verb, is a category by virtue of the fact that it refers to specific things on the basis of their properties. In the case of number, the essential property is the countable item, action or event, independent of its physical attributes. Thus, the category seven can refer to seven dolphins, seven pecks, seven sins, seven wonders of the world, seven days or seven licks on an ice-cream cone.

But do animals have a number concept? Could the pigeons understand that to peck one less than three times for a pellet requires them to peck twice? A number concept represents a symbol that has a particular relation to other symbols within the number domain. Like nouns and verbs that hold a particular relation to each other in the structure of a sentence (the domain of grammar), number concepts have unique roles by virtue of the arithmetical operations performed upon them. Thus, the concept of seven is unique because it is a prime number, the sum of one plus six, the number of pigeons left when two leave a flock of nine, and the only integer that is less than eight and greater than six. The category/concept distinction is important because a human child pointing to a flock of pigeons and saying seven may know that there are seven pigeons, but she may not know that this represents one less than a flock of eight pigeons, six more than one pigeon, and so forth. The same argument applies to animals pressing a button seven times or touching a symbol for seven on a screen.

Recent experiments by psychologists Elizabeth Brannon and Herb Terrace of Columbia University show that captive rhesus monkeys can understand the ordinal relations among the numbers one to nine. In the first phase of their experiment, experimenters presented the subject with a touch-sensitive monitor showing four different images. Each image displayed a different number of objects, varying from one to four. If the subject touched the images according to their ordinal relations—1, 2, 3, 4—it was rewarded. To ensure that subjects were attending to number, rather than some other feature, the experimenters varied size, color, and shape of the objects within each image. For example, in one trial there might be one large blue square, two small red triangles, three horses and four tiny circles. The rhesus monkeys' performance was excellent—but only after receiving hundreds of training trials.

Next, in the critical-generalization condition, the team introduced novel numbers and number combinations to the trials. Thus, in addition to seeing images with one to four objects, the rhesus monkeys now saw images with five to nine objects. Once again, Brannon and Terrace forced the monkeys to attend to number by varying size, shape and color of the objects. Surprisingly, the rhesus maintained their high level of performance, correctly pressing the images in ordinal fashion. Whether they see 1, 4, 7, 8 or 5, 6, 7, 8, the monkeys respond correctly. Clearly, rhesus monkeys are capable of understanding the principle of ordinality for the numbers one to nine.

Given that animals have limited spontaneous numerical abilities. which with training improve dramatically, we must return to a question first posed earlier: What kind of evolutionary or ecological pressures would have favored the numerical competence found in Homo sapiens? I suggest that in nature animals confront situations where relative, rather than absolute, quantification is sufficient. In many amphibian and fish species, for example, extremely large numbers of eggs are laid and guarded, and parents are aware of neither the initial number of eggs laid nor the number that have died or been removed by predators. Many avian species have their nests parasitized by a member of another species, one example being the cuckoo. Rather than rear its own young, the cuckoo deposits its eggs in a foreign nest, allowing the host parents to incubate and feed its young. Sometimes the parasite does a one-for-one swap, knocking out the host egg and replacing it with one of its own. In other cases, eggs are added without removing a host egg, or the number of eggs added exceeds the number removed. Despite the number differences in a parasitized nest, there is no evidence that the host shifts allocation of parental care. The host parents don't seem to be counting at all! For most species, parental investment appears to be guided by approximations rather than absolute numbers.

While competing for resources, animals track only a small number of individuals: a few competitors of higher or lower rank, a coalition of two or three allies and a small number of potential mates. In a troop of 50 baboons, individuals might notice the disappearance of a troop member but are unlikely to think "Geez, we're down to 49. That puts us at a disadvantage against our neighbors who have 50." It seems highly unlikely, therefore, that animals living under natural conditions would confront ecological problems that would select for greater numerical competence. But, as has been shown, it is quite possible to elicit exceptional numerical abilities in animals through training in a laboratory environment.

Countdown to a Combinatorial System

What mechanisms evolved in our most immediate ancestors that enabled them to represent and conceptualize numbers with greater competence than their animal neighbors? At this point, we can only offer a highly speculative answer to this question.

People are endowed with two cognitive talents that animals naturally lack: first, the capacity to spontaneously assign arbitrary symbols to objects and events in the world, and second, the ability to manipulate the sequence and order of a string of those symbols to alter their meaning—a combinatorial system. The explosion in a child's numerical competence, lacking in monkeys and apes, arises from her capacity to formally manipulate symbols. As she amasses a growing lexicon and learns to manipulate words, the child acquires the ability to juggle number symbols. Some of the basic elements of the number system are in place before the elements of language have been fully mastered. For example, a child understands that any solid object or discrete action, such as a star in the sky or the bounce of a basketball, can be counted—the principle of property indifference—but non-solid objects like sand, water and pudding cannot. It is for this reason that a child knows to ask for two bowls of pudding but not for two puddings. In contrast, more abstract elements of number emerge after the child has acquired a reasonable command of words. A child may not, for instance, have developed the concepts of count sequence and cardinality, in which the last label applied to the sequence represents the total number of items counted. Consequently, after counting a plate full of cookies and saying that there are "five," she will start counting again from one when asked the total number on the plate. In this sense, a child's numerical abilities are less mature than her linguistic abilities. The pattern of development proceeds with some aspects of numerical competence emerging before linguistic competence, and others emerging afterwards.

The combinatorial engine underlying our number and language systems allows for a finite number of elements to be recombined into an infinite variety of expressions. The evolutionary origin of this capacity remains unclear. Did it evolve for number, language or both? Clearly, the number system of animals shows no sign of combinatorial power, nor do their natural communication systems show any sign of combinatorial organization. At present, therefore, research on animals does little to further our understanding of this evolutionary mystery, but developmental data on children help a bit. Because children are capable of producing sentences long before they grasp the idea of counting, it would appear that recombination occurs first in the language system and then, somewhat later, in the number system. Studies of brain-damaged patients show that some individuals may suffer linguistic deficits without significant loss of numerical competence. Conversely, other individuals might be inflicted with severe numerical deficits while maintaining functioning linguistic abilities. This suggests that separate computational systems are responsible for language and number.

What I propose is that the selective pressure responsible for the emergence of a numerical combinatorial system, one that allowed ancestral humans to enumerate at a more precise level than other animals, is the emergence of exchange systems—trading, to be precise. Whether trading spears, mongongo nuts, goats for a dowry or coins, it is essential to know how much you are getting and that it is a fair exchange. Approximations are doomed to failure in this kind of system. And although some animals do engage in reciprocal exchanges, they are not based on any kind of quantitative precision. Vampire bats regurgitate blood to those that have regurgitated to them in the past, but they don't count milliliters. Bonobo males trade access to food for sex, but they don't count the amount of food dispensed nor tally the number of resulting copulations. In all of these interactions, the system functions on the basis of approximate returns. When social exchange of material goods came onto the scene, selection favored those individuals capable of enumeration and combinatorial computation with symbols. Early humans evolved to demand precise reciprocal exchange, providing the groundwork for a multitude of extraordinary mathematical systems.

Today, while sitting in mathematics classes or perusing library bookshelves, we can study trigonometry, algebra, calculus and set theory. These systems showcase the endless creativity of the human mind and its invention of symbolic notation. We must not forget, however, that such systems stand on a foundation left behind by our animal ancestors. At present we do not understand how these two domains of knowledge affect each other during the course of evolution or that of development. Some day we will.