The New Language of Mathematics
By Daniel S. Silver
Is it possible to take all words out of mathematical expressions?
Is it possible to take all words out of mathematical expressions?

Something strange is happening in mathematics seminar rooms around the world. Words and phrases such as spider, birdtrack, amoeba, sandpile, and octopus decomposition are being heard. Drawings that resemble prehistoric petroglyphs or ancient Chinese calligraphy are being seen, and are being manipulated like the traditional numerals and symbols of algebra. It is a language that would have been alien to mathematicians of past centuries.

Robert Garrigus / Alamy Stock Photo; Wikimedia Commons
The words and symbols of mathematics are intended to stimulate thought, promote curiosity, or simply amuse. At times they ignite public imagination. Occasionally they interfere with understanding. Always they are evolving. Today, as the boundaries of mathematical inquiry expand, their evolution seems to be accelerating. The words and symbols of mathematics have helped bring the subject to its present, bountiful state. But the question remains: Can the symbols of mathematics stand up on their own, without any words to support them?
Josiah Willard Gibbs navigated confidently in a sea of mathematical words and symbols. Gibbs was a founder of statistical mechanics and a professor of mathematical physics at Yale University during the latter half of the 19th century. Colleagues knew this outwardly plain and unassuming scholar as someone who rarely made public pronouncements. Imagine their surprise when, during a faculty meeting about replacing mathematics requirements for the bachelor’s degree with foreign language courses, Gibbs rose and forcefully declared: “Gentlemen, mathematics is a language.”

Wikimedia Commons
Gibbs wasn’t the first notable scientist to call mathematics a language. Galileo Galilei beat him to it by more than 200 years. In Il Saggiator (The Assayer), published in Rome in 1623, the Italian astronomer wrote: “[The universe] cannot be read until we have learned the language and become familiar with the characters in which it is written. It is written in mathematical language.”
Galileo wrote in Italian rather than scholarly Latin, hoping to reach readers who were literate but not necessarily scientific. But just as students at Plato’s Academy were reputedly greeted with the warning “Let no one ignorant of geometry enter here,” so Galileo’s readers were being cautioned that the book before them had some language prerequisites. For Galileo, the letters of mathematics were triangles, circles, and other geometric figures. Gibbs, who is responsible for much of the vector calculus that we use, would have added a modern symbol or two of his own.
If mathematics is a language, then just as any ordinary language, such as French or Russian, does not rely on another one to be understood, so mathematics should be independent of ordinary languages. The idea does not seem so far-fetched when we consider musical notation, which is readable by trained musicians everywhere. If mathematics is a language, then we should be able to understand its ideas without the use of words. Let’s see how that might be done.
Consider the task of adding the first few integers, say 1, 2, 3, 4, 5. Easy enough. Their sum is 15. But what about adding the first 100 integers?

Image courtesy of the author.
The figure at right displays 1 + 2 + 3 + 4 + 5 dots twice, once in black and again in red. By arranging all in rectangular fashion as we have, it is an easy matter to count the total, which is 5 × 6 = 30. In order to find our original sum, we need only divide by 2, thereby correcting for our double counting.
The novelty of the picture is that we can grasp the idea at a glance. Moreover, there is nothing special about 5 columns of dots. We could just as easily imagine 100. So 1 + 2 + . . . + 100 must be equal to 100 × 101 divided by 2, which is 5,050. Similarly we can find the sum of the first N integers, for any N whatsoever. The answer is N (N + 1) / 2.
Just as the 19th-century musician Felix Mendelssohn enjoyed writing Lieder ohne Worte (Songs Without Words), so mathematicians like to craft Proofs Without Words. Since 1975 the Mathematical Association of America has published a column devoted to them in its Mathematics Magazine. Its examples are intended to leave the reader speechless.
Despite the many proofs without words, mathematical thought ohne Worte might be impossible. Words come to us automatically when we view images. Images come to mind when we see words. It seems that we need words after all.
The role that words play in mathematics was on the mind of the French mathematician Jacques Hadamard when, during the 1940s, he asked colleagues around the world how they thought about their subject. Did they think in images or think in words? He summarized his findings in The Psychology of Invention in the Mathematical Field. One of the respondents was Albert Einstein, who wrote:
The words or the language, as they are written or spoken, do not seem to play any role in my mechanism of thought. The psychical entities which seem to serve as elements in thought are certain signs and more or less clear images which can be “voluntarily” reproduced and combined.
Even those mathematicians who would agree with Einstein recognize the severe limitation on thought imposed by the use of images alone. In 1983 the New Zealander and American mathematician Vaughan Jones made the point by reproducing the image of a big black dot to illustrate the projection lattice of II1 (read as “type two-one”) factors, a sophisticated algebraic object that Jones later used to create new tools for knot theory, which won him the prestigious Fields medal seven years later. Although the dot was not entirely gratuitous—it came about by thinking of factors in terms of concentric black circles—it was intended as a humorous commentary on the constraints of imagery. “Some people have enjoyed the joke,” Jones told me.
Whether or not mathematics is a language, its words share with ordinary language an important function: They transport essential images from one mind to another. For that reason the choice of words that we make is important.
In 1948, Claude Shannon, working on communication theory at Bell Telephone Laboratories, created a beautiful and useful algebraic expression for a measure of average uncertainty in an information source. Its similarity in form to the statistical mechanics notion of entropy, introduced by Rudolf Clausius in 1864, was noted with wonder by many, including the mathematician John von Neumann. Shannon is said to have told an interviewer the following anecdote in 1961:

Photograph courtesy of Tekniska museet/Flickr cc.
My greatest concern was what to call it. I thought of calling it “information,” but the word was overly used, so I decided to call it “uncertainty.” When I discussed it with John von Neumann, he had a better idea. Von Neumann told me, “You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, no one knows what entropy really is, so in a debate you will always have the advantage.”
Although von Neumann’s second reason presumably was intended as a joke, the exchange highlights the importance of careful language choice in fostering understanding. Like Shannon, many mathematicians agonize over the words they invent, hoping those they choose will survive for decades. Shannon’s choice proved to be brilliant for three reasons, two in addition to those proposed by von Neumann.
First, mathematicians enjoy the borrowed authority of words from science, especially from physics. Von Neumann was correct when he said that the use of entropy conferred an advantage on the speaker. Audience members either know the meaning of the term or else they feel that they should.
Second, Shannon’s appropriation of the term entropy provoked an insightful debate. Did his term in fact have a meaningful connection with statistical mechanics? The debate has been productive. Today Clausius’s entropy is regarded by many as a special case of Shannon’s idea.
Third, the wide popularity of Shannon’s information theory has been helped by his use of a word that is recognized, if not truly understood, by everyone. Its associations with disorder in everyday life evoke a sympathetic response, much like another popular mathematical word, chaos.
“Must a name mean something?” asked Alice doubtfully. “Of course it must,” was Humpty Dumpty’s emphatic reply to Alice’s question in Lewis Carroll’s Through the Looking-Glass.
Mathematician James Yorke of the University of Maryland would have given Alice the same answer. In a recent discussion I had with him, Yorke recalled his decision to adopt the word chaos for a mathematical phenomenon associated with a type of unpredictable behavior found everywhere in the world, from the drip patterns of water faucets to long-range weather behavior. “Your terms should mean something,” he insisted. He dismissed the advice of colleagues urging him to choose a more dispassionate term. Yorke wished to capture the feelings that we all have about the randomness in our lives.
Mathematical monikers usually slip through the world quietly, recognized only by the researchers who use them. Chaos was an exception. In 1975 Yorke and his coauthor, mathematician Tien-Yien Li of Michigan State University, proved a surprising theorem about continuous functions on an interval, the sort of functions that students learn about in calculus. They wrote up their proof in a short paper titled “Period Three Implies Chaos.”
Mathematical monikers usually slip through the world quietly. The term chaos was an exception; it seized the public imagination.
What did Yorke and Li prove? Think of such a function as a machine: Insert a number a from the interval and get a value b. If we put b into our machine, then we get a third number c. Now insert c to get d. If it happens that d is equal to a, then we say that a has period three. In a similar way, a number might have period four, five, or any other number. What Yorke and Li proved, assuming continuity, is that if some number has period three, then one can find numbers of any period one chooses.
Yorke and Li also showed that many numbers have successive outputs that never return to their starting value. More surprisingly, pairs of such non-periodic numbers can be found as close together as desired, yet having successive outputs that move apart. It is an example of sensitive dependence on initial conditions. The situation is, well, chaotic.
Had Yorke and Li published their paper in a specialists’ journal in their field of dynamical systems, it is likely that chaos would never have caught the public’s imagination. Few people know that the word had already appeared with another meaning in the wonderfully oxymoronic title “The Homogeneous Chaos.” The author was Norbert Wiener, the creator of cybernetics.
Wiener published his article in the 1938 volume of the research-oriented American Journal of Mathematics. Instead Yorke and Li published in the American Mathematical Monthly, an expository journal published by the Mathematical Association of America, intended for a broad readership, from college students to researchers. When biologist Robert May read the article and wrote about its implications for population models a year later in the journal Nature, the word chaos appeared on top of the first page. According to Yorke, that is when the term took off.
How long does it take a mathematical word to seize the public imagination? Within 10 years, James Gleick’s Chaos: Making a New Science would become a bestseller. The book, which marks its 30th anniversary this year, celebrated its subject, beginning with the ideas of mathematician and meteorologist Edward Lorenz. In 1961 Lorenz had noticed that over extended periods of time, his model of weather patterns behaved differently when its initial conditions were varied only slightly. Although such a phenomenon was not new to mathematicians—the French mathematician Henri Poincaré had written about it at the turn of the 20th century—it came as a shock to many scientists. Storm conditions today, Lorenz suggested, might have been caused several weeks ago by a butterfly flapping its wings in Brazil. Butterfly effect was the term he coined to reinforce the metaphor.
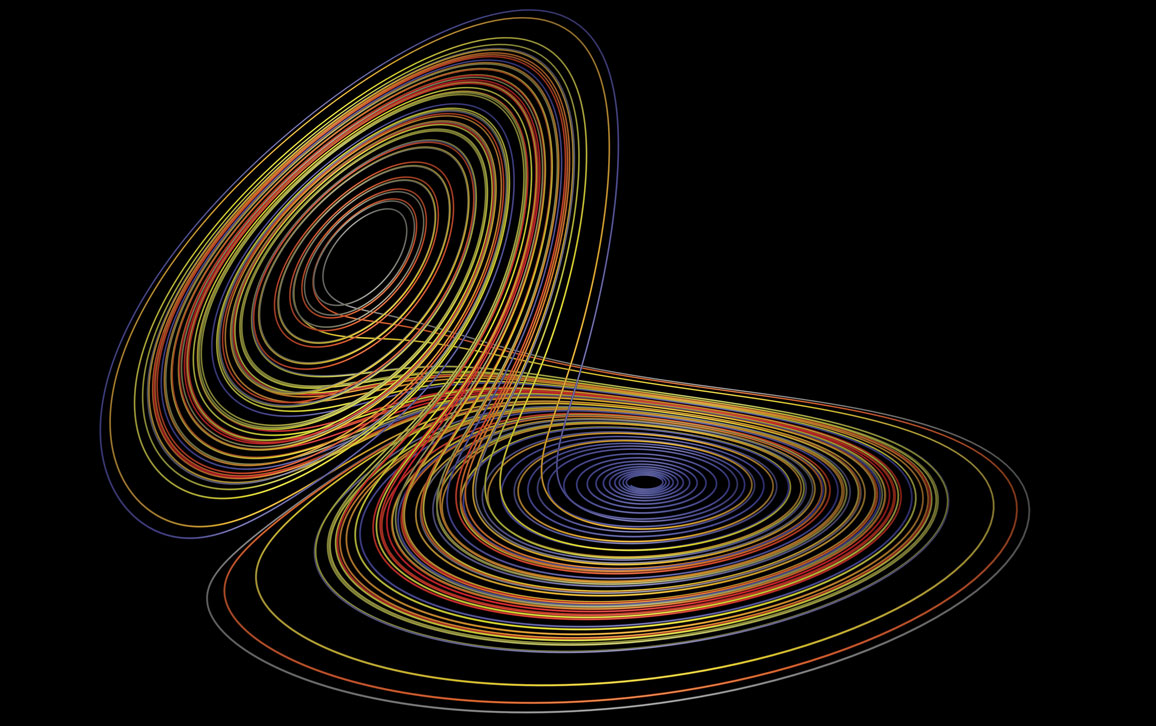
Image by Paul Bourke.
If a mathematical term is to catch fire with general readers, it must spark their imagination. A powerful image helps. In the case of chaos, Lorenz himself had supplied it. It was a bundle of curves, today called the Lorenz attractor, suggesting the infinite number of solution curves to a system of three differential equations. And it resembled the two wings of a butterfly. Start at any point of one of its solution curves and follow around, and you visit the two wings successively in some infinite pattern. Start at a nearby point on a different curve and the pattern might become wildly different after some time. The Lorenz attractor became the emblem of a new and lasting field, chaos theory.
Poorly chosen words and phrases can interfere with the progress of mathematics. René Descartes showed us how.
While pondering solutions to algebraic equations, Descartes was compelled to consider the possibility that some numbers when multiplied by themselves could give a negative result. Certainly no “real numbers,” that is, no numbers on the familiar number line, behave that way. Descartes called the numbers imaginaire (imaginary). In La Géométrie, his effort in 1637 to unify geometry and algebra, he explained that “true or false roots can be real or imaginary.”
The expression imaginary number caught on. Carl Friedrich Gauss, one of the greatest mathematicians of all time, despised it. In 1831 Gauss wrote, “If this subject...[has been] enveloped in mystery and surrounded by darkness, it is largely an unsuitable terminology which should be blamed.”
Gauss preferred the less censorious term complex numbers, which includes both ordinary (real) numbers and imaginary numbers appearing together in a single expression, such as two plus the square root of negative three. Regrettably, Descartes’s coinage remains in circulation, adding to the handicap that mathematics teachers endure as they try to convince some students that complex numbers are more than imaginary, having significant applications throughout the sciences.
In 1670 Isaac Newton contributed the intensely bothersome words fluents, fluxions, and even ffluxions. They were intended to describe the path and velocity of fluid in motion, but defining them rigorously proved too difficult even for the Cambridge genius. For more than a century mathematicians tried and failed to clarify the meanings of these words with their implied metaphysical notions of time. During the 1800s, rigorous and effective definitions, those of limit and derivative, were finally developed without the mention of time, and mathematicians stopped using Newton’s f-words.
British mathematicians of the 19th century loved inventing new words and phrases for mathematical concepts. Unfortunately, they got off to a rather bad start.

Calvin and Hobbes © 1994 Watterson. Reprinted with permission of Andrews McMeel Syndication. All rights reserved.
In 1801 a book by Cambridge professor John Colson, who held the Lucasian Chair of Mathematics (earlier held by Newton and later by Stephen Hawking) was published as an English translation of Instituzioni analitiche ad uso della gioventú italiana (Foundations of Analysis for the Use of Italian Youth), a textbook about calculus written by Maria Agnesi in 1748. It is a pity that Colson didn’t know much Italian. He learned just enough to follow the path of translation, dropping a hazardous rock onto the road along the way.
In her book Agnesi had described a particular curve, referring to it as “la curva...dicesi la Versiera.” The word versiera was an adaptation by another Italian author, Guido Grandi, from the Latin word versoria, meaning “a rope that turns a sail.” It was a helpful image. Colson could not find Agnesi’s “la versiera,” because it was not in any dictionary. He used the closest word that he could find, l’avversiera.
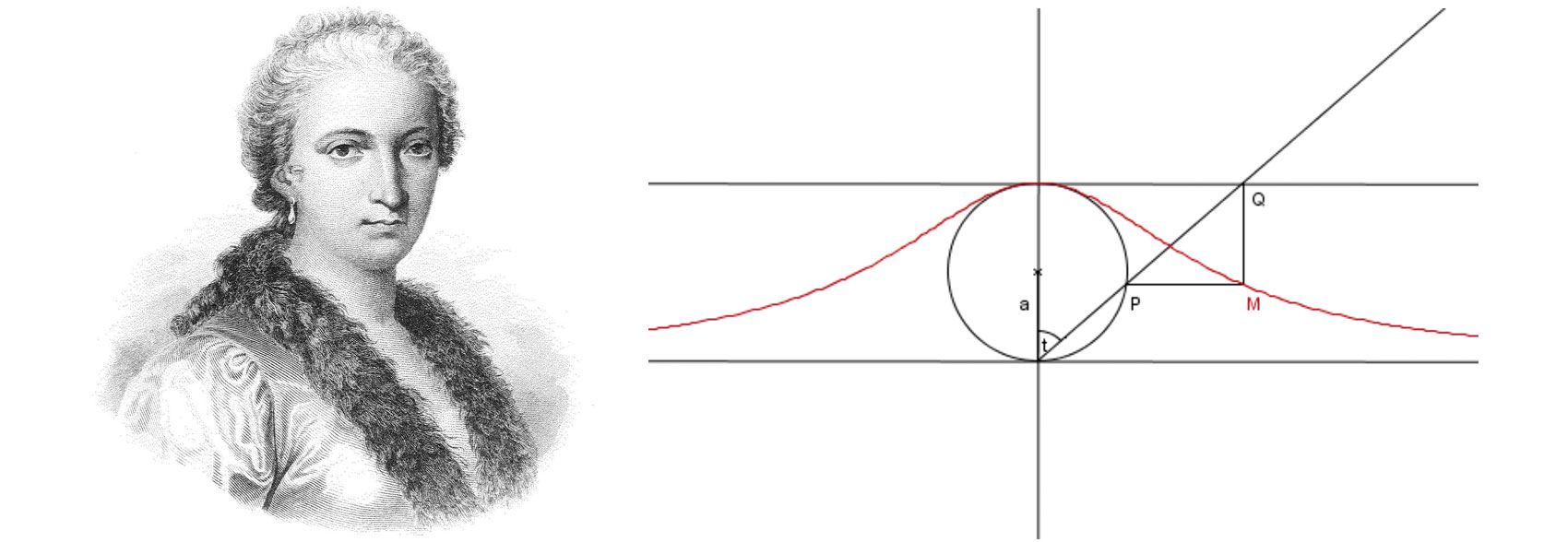
Maria Gaetana Agnesi (left) authored a mathematics textbook in Italian in 1748. In the volume she describes a particular curve (right), calling it la versiera, and adaption from the Latin word versoria, meaning a rope that turns a sail. But when her textbook was translated into English by Cambridge mathematician John Colson and published in 1801, he mistook the word for another that means “the witch.” The mistranslated moniker still sticks with the curve in modern textbooks, which call it Witch of Agnesi, to the confusion of students who are not told of the reasons for any supernatural connections. The story demonstrates the importance of choosing potential mathematical terms with care.
Wikimedia Commons
In Italian l’avversiera means “the witch” or “the she-devil.” Colson’s text thus referred to “the equation of the curve to be described, which is vulgarly called the Witch.” Today’s calculus textbooks continue to use the term Witch of Agnesi, and students continue to stare at the curve and wonder what demonic forces shaped it. It is ironic that Agnesi was a devout woman who spent most of her adult life aiding the poor.
No British mathematician was a greater wordsmith than James Joseph Sylvester. Born in London in 1814, he attended Cambridge University but could not be awarded a degree because, as a Jew, he did not subscribe to the Thirty-Nine Articles of Religion of the Anglican Church. He managed to support himself by teaching at the secular University College London and working as an actuary. Finally, in 1876, Sylvester’s career reached its full promise when he was appointed to a professorship at the new Johns Hopkins University in Baltimore, Maryland. There he began the United States’ first mathematics research department and its first mathematics research journal, the aforementioned American Journal of Mathematics.

Chris Hellier / Science Source
Sylvester loved language almost as much as mathematics. He composed unappreciated poetry, and in 1870 he proudly self-published a slim volume, The Laws of Verse, in which he proposed rules for effective versification. Not surprisingly, Sylvester coined many mathematical words. At the end of his article “On a Theory of the Syzygetic Relations of Two Rational Integral Functions,” published in 1853, he attached a glossary of “New or unusual Terms, used in a new or unusual sense in the preceding Memoir.” It began with allotrious, apocopated, bezoutic, sprinkled monotheme, perimetrical, rhizoristic along the way, and finished up with umbral, weight, and zeta.
Most of Sylvester’s words have been forgotten, but some have survived. Perhaps his most notable contribution to mathematic’s lexicon is matrix, a square or rectangular arrangement of terms in rows and columns. It is a Latin word that means womb. Sylvester was most interested in the case of a square matrix, one for which the numbers of rows and columns are equal. Because a rectangular matrix can give birth, so to speak, to a square matrix by striking out unwanted rows or columns, matrix, with its suggestion of fertility, seemed appropriate.
The word matrix lives on in mathematics at all levels. And like chaos, it has captured popular imagination. Sylvester would have been delighted to know that at the end of the 20th century both a Hollywood science-fiction film and a compact car would carry the name.
The symbols of mathematics appear to be separate from the words alongside them. In fact, they have evolved from words. The 19th-century German philologist and historian Heinrich Nesselmann was the first to recognize this concept. He identified three stages of their evolution: rhetorical, syncopated, and symbolic.
An illustration of Nesselmann’s theory is furnished by the humble minus sign that we use for subtraction. In medieval Europe the operation of subtraction was written out; we find it recorded as minus (Latin), moins (French), or meno (Italian). However, by the 15th century, the word had been syncopated, shortened to m–. The symbol – began to replace m– as early as 1489, the year that Johannes Widmann published a book of commercial arithmetic with the phrase (in translation): “What – is, that is less, and the + is more.”
It is a common and uncomfortable experience for someone presenting a pictorial argument to hear a skeptic ask, “Is that really a proof?”
No matter what their origin, symbols have been a source of mystery for mathematicians. They do more than merely stand in for words. Gottfried Wilhelm Leibniz, who shares with Newton credit for discovering calculus, believed it. Leibniz was so smitten by symbols that he dreamed of a purely symbolic language, one with which nations might someday settle arguments, using computation rather than swords and cannon. He imagined an alphabet of ideas.
Leibniz never found his universal language, but others have had success searching for ideographic languages with more specialized functions. The German mathematician and philosopher Gottlob Frege thought that he had found a way to communicate with just symbols. In 1879 he published Begriffsschrift, an 88-page booklet in which the quantifiers of formal logic first appeared. Frege described his work as “a formula language, modeled on that of arithmetic, of pure thought.” Diagrams stretched not only across its pages but up and down them as well.
Today Frege’s work is regarded by many as the most important single work in logic. However, in its day, the book was derided. Logician John Venn (remembered today for his eponymous diagrams) described Begriffsschrift as “cumbersome and inconvenient.” Another influential logician, Ernst Schröder, called it a “monstrous waste of space” and complained that it “indulges in the Japanese custom of writing vertically.”
Frege faced resistance not just from readers. His two-dimensional formulas and other exotic symbols precipitated complaints from his typesetter. “After all, the convenience of the typesetter is certainly not the summum bonum [highest good],” Frege argued some years later. Costs associated with typesetting, once a bane for mathematicians, have disappeared today thanks to effective software that enables authors to create camera-ready manuscripts for journals and periodicals. Nevertheless, the mathematical community’s reluctance to adopt pictorial arguments has slowed their acceptance.
Wikipedia
Pictures have accompanied mathematical proofs since the days of Euclid. But a picture can mislead us by suggesting that the special case it illustrates is sufficiently general for our argument. Beginning in the late 19th century, intuition-defying examples from the expanding subject of topology reinforced doubts about our spatial intuition and proofs that rely on them. Giusseppe Peano’s space-filling curve was one such example: Try to imagine an unbroken curve inside a square that does not miss a single point. Few can, but Peano could. He constructed such a curve using an infinite recursive process. No picture can fully describe it. (More about Peano can be found in “Crinkly Curves,” Computing Science, May–June 2013.)
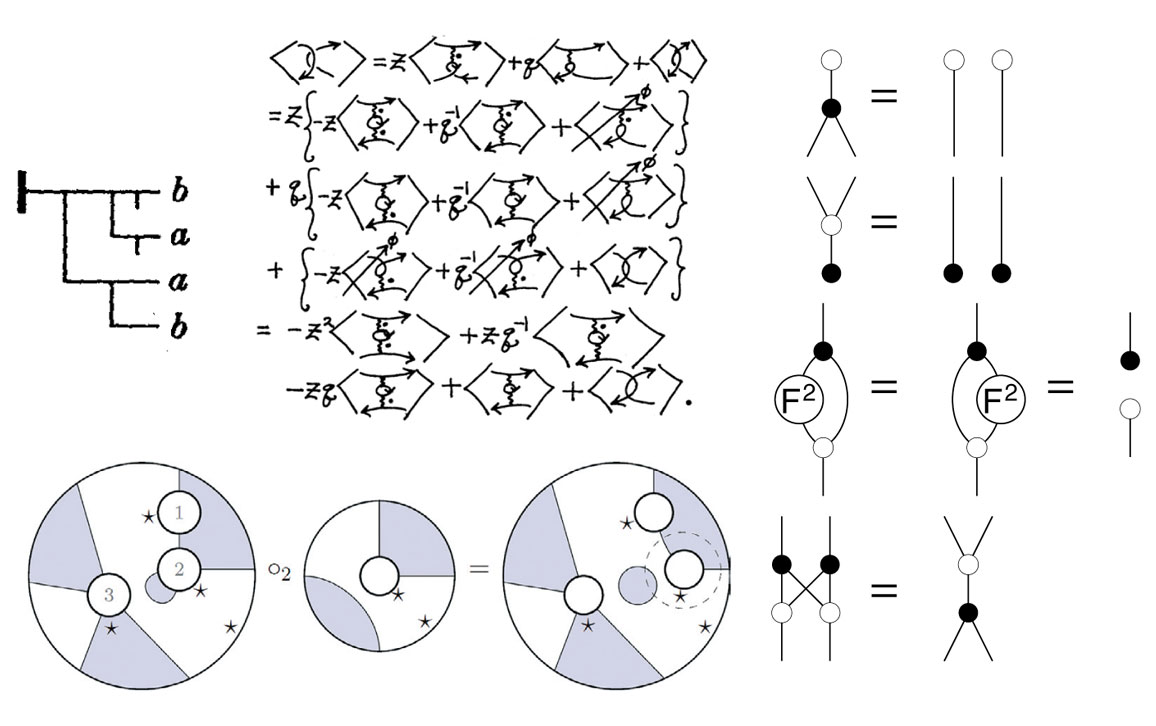
Mathematicians’ reluctance to accept images in place of words has softened but not vanished. It is a common and uncomfortable experience for someone presenting a pictorial argument to hear a skeptic ask, “Is that really a proof?” Predrag Cvitanović of Georgia Institute of Technology knows the experience. He recalls the taunt of a colleague staring at the pictograms that he had left on a blackboard: “What are these birdtracks?” Cvitanović liked the ornithological term so much that he decided to adopt it for the name of his new notation.
So what are these birdtracks? Briefly, they are combinations of dots, lines, boxes, arrows, and other symbols, letters of a diagrammatic language for a type of algebra. They were inspired by the famous paper about QED, written in 1948 by physicist Richard Feynmann, and also later articles by mathematical physicist Roger Penrose. As Cvitanović explained in his 1984 book, Group Theory: Birdtracks, Lie’s, and Exceptional Groups, the diagrams represent an evolution of language. They are not merely mnemonic devices or an aid for computation. Rather, they are “everything—unlike Feynman diagrams, here all calculations are carried out in terms of birdtracks, from start to finish.” Could one perform the calculations without them? Yes, but as Cvitanović warns the reader, it would be like speaking Italian without using your hands.
Birdtracks are not the only picture-language game in town. Others have been, and are being, invented for different purposes. Louis H. Kauffman, a mathematician at the University of Illinois at Chicago and one of the most inventive and influential topologists of our time, uses a variety of new diagrammatic languages for the study of knots. An algebraist familiar with birdtracks would recognize much but not all of what she might read in Kauffman’s book Formal Knot Theory, much as a traveler might understand spoken cognates of a foreign tongue.
Planar algebras are another significant picture language. Jones (the one with the big black dot mentioned earlier) introduced them in 1999, and they provide a general setting for important quantities in the study of knots. The basic pictures of the language are planar tangles—disks with smaller disks inside them—connected by line segments and decorated with stars and shading. Planar tangles can be combined to form new characters. The properties they exhibit mirror those of different algebraic and topological structures that are already familiar to researchers. Consequently, planar algebras have a variety of applications.
Birdtracks and planar algebras are picture-languages that draw their initial inspiration from physics. Yet another is quon language, first introduced in December 2016 on arXiv.org, a repository of online research-paper preprints that is used by scientists throughout the world. Quon language, created by Harvard University mathematicians Zhengwei Liu, Alex Wozniakowski, and Arthur M. Jaffe, is derived from three-dimensional pictorial representations of particlelike excitations and transformations that act on them. An earlier, simpler version has much in common with the languages of Cvitanović and Kauffman.
According to its inventors, the quon language can do more than aid in the study of quantum information. It is also a language for algebra and topology, with the ability to prove theorems in both subjects. In an interview with the Harvard Gazette, Jaffe remarked, “So this pictorial language for mathematics can give you insights and a way of thinking that you don’t see in the usual, algebraic way of approaching mathematics.” He added that “It turns out one picture is worth 1,000 symbols.”
Something strange is indeed happening in mathematics seminar rooms today, but it amounts to more than amusing sights and sounds. Mathematicians are attempting to break through the barriers of traditional language in order to think more deeply about fundamental questions. Their strange words and images are attracting attention, motivating all of us to learn more about them.
Leibniz was so smitten with symbols that he dreamed of a purely symbolic language, one with which nations might someday settle arguments, using computation rather than swords and cannon.
In a series of lectures at Cornell University in 1965, Richard Feynman contemplated the effectiveness of mathematics in science. He sympathized with the lay reader who asked why it was not possible to explain mathematical ideas with ordinary language. Correcting Gibbs, who started our discussion, Feynman replied that it is “because mathematics is not just another language.” Simply put, mathematics is more general than any language that tries to express it.
Traditional methods of learning mathematics are discursive, demanding a sequential, step-by-step understanding. Assuming that a lesson succeeds, there is a moment of “aha!” when lights turn on and the room is illuminated for us. One day it might become possible to flip on the light switch as soon as we enter the room. Philosopher and logician Susanne K. Langer once called for a revolution in our modes of communication, moving beyond our “tiny, grammar-bound island.” Our journey from words to symbols to picture language is bringing Langer’s revolution just a bit closer.
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.