The Humpty-Dumpty Problem
By Robert Dorit
Even when we understand their parts, living things are hard to put back together
Even when we understand their parts, living things are hard to put back together

DOI: 10.1511/2011.91.293
The publication in 1637 of René Descartes’ Discourse on the Method of Rightly Conducting One’s Reason and of Seeking Truth in the Sciences changed the practice of science forever. In it, he poured the foundations of modern science by putting forth two powerful and interrelated theses. The first embraced reductionism as a way of knowing: Descartes committed himself to “divide each of the difficulties under examination into as many parts as possible, and as might be necessary for its adequate solution,” and to “conduct my thoughts in such order that, beginning with those objects that are simplest and most readily understood, I might ascend little by little, and, as it were, step by step, to the knowledge of the more complex.” Later in the same work, he deployed one of the most durable metaphors of Western intellectual thought: He argued that the body was best thought of as a machine.

Illustration by Tom Dunne.
By coupling those two ideas—that complex machines could be understood by taking them apart, and that living beings are essentially machines—Descartes set the stage for the age of science. He argued persuasively that living systems emerge as the physical consequences of material forces. For example, also in his Discourse, he explained the workings of the heart:
I wish it to be considered that the motion which I have now explained follows as necessarily from the very arrangement of the parts, which may be observed in the heart by the eye alone, and from the heat which may be felt with the fingers, and from the nature of the blood as learned from experience, as does the motion of a clock from the power, the situation, and shape of its counterweights and wheels.
The living world was thus the legitimate province of the sciences and its inner workings could be probed and understood through logic, observation and experiment.
The task of this new science would henceforth consist in disassembling the seemingly complicated machinery of life into its simplest components, which could then be cataloged, prodded, manipulated and described. According to Descartes’ model, any real understanding of the body could only come from taking it apart, just as one takes apart a machine to discover its inner workings. If we wish to understand how a clock tells time, according to this model, our job is to disassemble it. Understanding a clock means understanding its springs and gears. And the same is true of living “machines.”
This notion of the body as a machine would clear away centuries of intellectual detritus: By arguing that the body was the sum of its interacting parts, and, more importantly, by suggesting that the study of those parts would reveal the workings of the body, Descartes shifted centuries of scientific and philosophical discussion about imponderable life forces and inexplicable animist vapors. (Lest we go overboard in praising Descartes, he clearly panicked at the last moment. He exempted human beings from the ground rules he set for other living organisms. In so doing, he sowed 400 years of confusion and discord with his notion that the mind and the body were separate phenomena, governed by separate rules.)
Implicit in both the strategy of reductionism and the metaphor of the machine, however, is a hidden assumption. That assumption is that an accurate understanding of the parts will reveal the workings of the machine in their entirety. To state it differently, we do not need to be overly concerned with how we take the machine apart, because the parts themselves will dictate the reassembly. But is this assumption true?
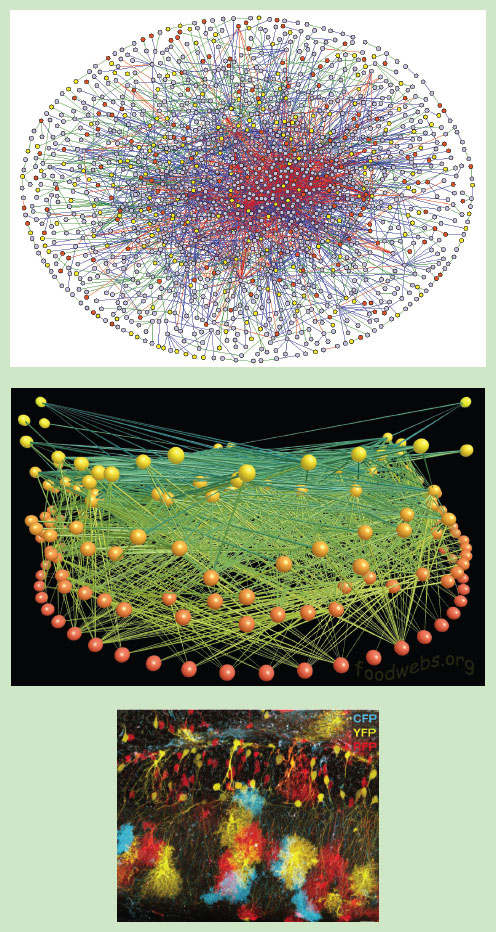
Top image from Ulrich Stelzl et al. and the MDC. Middle image was produced with FoodWeb3D, written by R. J. Williams and provided by www.foodwebs.org, Yoon et al. 2004. Bottom image reprinted by permission from Macmillan Publishers Limited: Nature, Livet et al., 2007.
Anyone who has tried to repair a piece of lab equipment, a washing machine or even an old-school carburetor knows the dangers of taking something apart without paying careful attention to the process. Making a couple of sketches or taking a few photographs during disassembly certainly makes life easier later on, when the goal is reconstruction. A little thought and a few disastrous reassemblies make it easy to dismiss the idea that the parts harbor the information needed to reassemble the whole. Yet the truth is complicated. I suspect that the reductionist strategy, in its purest form, does work when the number of component parts is comparatively small and their relations are limited and predictable. If a given gear can only mesh with a small number of other components, and a given spring fits only on a single stem, the parts do encode the whole. This is why a good clock maker could probably put a clock back together—even one she has never seen before—if all of the parts were laid out in front of her.
But living systems are not really clocklike in their assembly, and organisms are not really machines. Despite Descartes’ contention that we could not distinguish a well-made automaton of an ape from an actual ape (“were there such machines exactly resembling organs and outward form an ape or any other irrational animal, we could have no means of knowing that they were in any respect of a different nature from these animals”), the relations of parts to wholes in living systems is entirely different from that in machines—and most unclocklike.
If anything, living systems consistently violate all of the criteria for reducibility. The number of elements that compose any living system—an ecosystem, an organism, an organ or a cell—is enormous. In living systems, the specific identities of these component parts matter. Unlike chemistry, for instance, in which an electron in a lithium atom is identical to an electron in a gold atom, all proteins in a cell are not equivalent or interchangeable. Each protein is the result of its own evolutionary trajectory. We understand and exploit their similarities, but their differences matter to us just as much. Perhaps most importantly, the relations between the components of living systems are complex, context-dependent and weak. In mechanical machines, the conversation taking place between the parts involves clear and unambiguous interactions. These interactions result in simple causes and effects: They are instructions barked down a simple chain of command.
In living systems, by contrast, virtually every interesting bit of biological machinery is embedded in a very large web of weak interactions. And this network of interactions gives rise to a discussion among the parts that is less like a chain of command and more like a complex court intrigue: ambiguous whispers against a noisy and distracting background. As a result, the same interaction between a regulatory protein and a segment of DNA can lead to different (and sometimes opposite) outcomes depending on which other proteins are present in the vicinity. The firing of a neuron can act to amplify the signal coming from other neurons or act instead to suppress it, based solely on the network in which the neuron is embedded. The disappearance of a single species can stabilize an ecosystem or send it spinning into chaos, depending on (you guessed it) the network of interactions that surrounds that species. This extensive and subtle connectivity, which gives meaning to the behavior of the underlying components, turns out to be a consistent feature of living systems.
The recurrent evolution of these networks of weak interactions suggests that they may allow biological systems to incorporate information from the environment while also maintaining stability in the face of constant perturbation. This general feature of living systems also has clear methodological consequences for modern biology. Once this gossamer web is taken apart in search of the smallest components we can study, the process of putting it back together bears no resemblance at all to reconstructing a clock. Thus we find ourselves, early in the 21st century, with extraordinarily detailed descriptions of the components of many biological systems. But reconstructing those systems is proving to be a monumental and consistently surprising enterprise.
The promise of reductionism rested on the belief that an intelligent dissection of complex phenomena would not only yield progress, but would eventually reduce any problem to its component parts. Complexity, we naively hoped, was simply a by-product of incomplete understanding, an illusion that would fall away once the parts were fully understood. But this is the dirty little secret of contemporary biology: Despite our reductionist successes, the central conceptual problems of biology have not yielded to study. We have revealed the elegant workings of neurons in exquisite detail, but the material understanding of consciousness remains elusive. We have sequenced human genomes in their entirety, but the process that leads from a genome to an organism is still poorly understood. We have captured the intricacies of photosynthesis, and yet the consequences of rising carbon-dioxide levels for the future of the rain forests remain frustratingly hazy. We are, in short, the king’s horses and the king’s men: We stare at the pieces, knowing what Humpty should look like, but unable to put him together again.
Despite its limitations, reductionism as a research strategy in biology has proven phenomenally successful. The ascendancy of the life sciences, from the discovery of DNA in 1954 to the sequencing of the human genome in 2003, attests to the power of the reductionist approach. We cannot and will not solve the central challenges of biology without understanding in detail how the component parts operate. My argument is not with reductionism itself, but with the idea that it represents the only viable strategy for understanding the living world. And here, too, I want to be careful: Some of the arguments about “irreducible complexity” or “emergence” flirt dangerously with pre- and post-Cartesian animist notions of life forces, ideas that lie beyond the realm of science. Acknowledging the limitations of reductionism does not an anti-materialist make. The living world in all of its contingency and beauty is still the material world and, as such, the result of material forces.
But the days when we could have blind faith in the power of reductionist deconstruction are over. Humpty lies in fragments. Fortunately for us, a new approach is taking shape to replace the seductive appeal of reductionism. We biologists may have bought a little too much of what Descartes had to sell, but as the limits of naive reductionism become more obvious, additional methods emerge for understanding the complexity of life. This new, interactionist perspective on living systems, with its emphasis on the interplay of parts, has benefited from new computational tools and experimental approaches. Whole new subfields in the life sciences, as well as productive interactions among existing disciplines, have emerged. Systems biologists, complexity theorists and newly minted biologists now attend as carefully to the ways in which parts come together as they do to the parts themselves. In the process, features of living systems that we once carelessly overlooked (or destroyed) in our haste to deconstruct now snap into focus. We are, for instance, beginning to understand that modularity and redundancy are inherent features of all levels of biological organization. These features characterize systems that are simultaneously resilient and capable of evolving. They are the calling cards of life.
The current emphasis on interactions also ushers in a new kind of conceptual harmony in biology. The latter half of the 20th century was marked by an apparent and unnecessary gulf between those branches of biology that studied parts—cells and molecules—and those that focused on organisms and ecosystems. The former, committed to reductionism, saw themselves as ascendant, as replacing descriptive natural history with rigorous, experimentally driven hard science. The latter, by contrast, seemed defensive. They were unwilling to concede the potential utility of the reductionist approach or to advocate for the importance of evolutionary history at all levels of biological organization. But now, chastened by experience, we have been reminded that the living world is neither wholly reducible nor fundamentally irreducible. Instead, we have come to understand through biology’s one Theory of Everything, evolution, that the unity and the diversity of the living world are inseparable. Evolution has crafted the very relation between parts and wholes that our science should seek to emulate: Neither is viable without the other. The questions we are asking as biologists are profound and profoundly difficult. Meaningless discussions about what kind of biology is best must give way to a more nuanced dialectic. It is time for a science as subtle as its objects of study.
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.