An Adventure in the Nth Dimension
By Brian Hayes
On the mystery of a ball that fills a box, but vanishes in the vastness of higher dimensions
On the mystery of a ball that fills a box, but vanishes in the vastness of higher dimensions

DOI: 10.1511/2011.93.442
The area enclosed by a circle is πr2. The volume inside a sphere is 4/3πr3. These are formulas I learned too early in life. Having committed them to memory as a schoolboy, I ceased to ask questions about their origin or meaning. In particular, it never occurred to me to wonder how the two formulas are related, or whether they could be extended beyond the familiar world of two- and three-dimensional objects to the geometry of higher-dimensional spaces. What’s the volume bounded by a four-dimensional sphere? Is there some master formula that gives the measure of a round object in n dimensions?
Some 50 years after my first exposure to the formulas for area and volume, I have finally had occasion to look into these broader questions. Finding the master formula for n-dimensional volumes was easy; a few minutes with Google and Wikipedia was all it took. But I’ve had many a brow-furrowing moment since then trying to make sense of what the formula is telling me. The relation between volume and dimension is not at all what I expected; indeed, it’s one of the zaniest things I’ve ever come upon in mathematics. I’m appalled to realize that I have passed so much of my life in ignorance of this curious phenomenon. I write about it here in case anyone else also missed school on the day the class learned n-dimensional geometry.
In those childhood years when I was memorizing volume formulas, I also played a lot of ball games. Often the game was delayed when we lost the ball in the weeds beyond right field. I didn't know it then, but we were lucky we played on a two-dimensional field. If we had lost our ball in a space of many dimensions, we might still be looking for it.
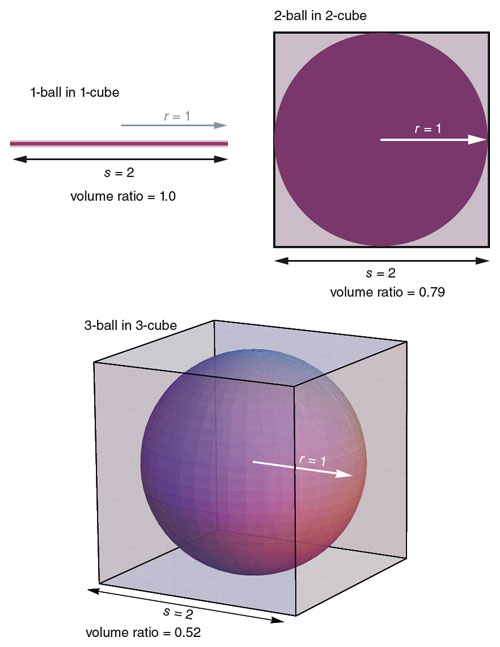
Illustration by Brian Hayes
The mathematician Richard Bellman labeled this effect “the curse of dimensionality.” As the number of spatial dimensions goes up, finding things or measuring their size and shape gets harder. This is a matter of practical consequence, because many computational tasks are carried out in a high-dimensional setting. Typically each variable in a problem description is mapped to a separate dimension.
A few months ago I was preparing an illustration of Bellman’s curse for an earlier Computing Science column. My first thought was to show the ball-in-a-box phenomenon. Put an n-dimensional ball in an n-dimensional cube just large enough to receive it. As n increases, the fraction of the cube’s volume occupied by the ball falls dramatically.
In the end I chose a different and simpler scheme for the illustration. But after the column appeared (“Quasirandom Ramblings,” July–August), I returned to the ball-in-a-box question out of curiosity. I had long thought that I understood it, but I realized that I had almost no quantitative data on the relative size of the ball and the cube.
(In this context “ball” is not just a plaything but also the mathematical term for a solid spherical object. “Sphere” itself is generally reserved for a hollow shell, like a soap bubble. More formally, a sphere is the locus of all points whose distance from the center is equal to the radius r. A ball is the locus of points whose distance from the center is less than or equal to r. And while I’m trudging through this mire of terminology, I should mention that “n-ball” and “n-cube” refer to an n-dimensional object inhabiting n-dimensional space. This may seem too obvious to bother stating, but some branches of mathematics adopt a different convention. In topology, a 2-sphere lives in 3-space.)
An n-ball of radius 1 (a “unit ball”) will just fit inside an n-cube with sides of length 2. The surface of the ball kisses the center of each face of the cube. In this configuration, what fraction of the cubic volume is filled by the ball?
The question is answered easily in the familiar low-dimensional spaces we are all accustomed to living in. At the bottom of the hierarchy is one-dimensional geometry, which is rather dull: Everything looks like a line segment. A 1-ball with r=1 and a 1-cube with s=2 are actually the same object—a line segment of length 2. Thus in one dimension the ball completely fills the cube; the volume ratio is 1.0.
In two dimensions, a 2-ball inside a 2-cube is a disk inscribed in a square, and so this problem can be solved with one of my childhood formulas. With r=1, the area πr2 is simply π, whereas the area of the square, s2, is 4; the ratio of these quantities is about 0.79.
In three dimensions, the ball’s volume is 4/3π, whereas the cube has a volume of 8; this works out to a ratio of approximately 0.52.
On the basis of these three data points, it appears that the ball fills a smaller and smaller fraction of the cube as n increases. There’s a simple, intuitive argument suggesting that the trend will continue: The regions of the cube that are left vacant by the ball are the corners. Each time n increases by 1, the number of corners doubles, so we can expect ever more volume to migrate into the nooks and crannies near the cube’s vertices.
To go beyond this appealing but nonquantitative principle, I would have to calculate the volume of n-balls and n-cubes for values of n greater than 3. The calculation is easy for the cube. An n-cube with sides of length s has volume sn. The cube that encloses a unit ball has s=2, so the volume is 2n.
But what about the n-ball? As I have already noted, my early education failed to equip me with the necessary formula, and so I turned to the Web. What a marvel it is! (And it gets better all the time.) In two or three clicks I had before me a Wikipedia page titled “Deriving the volume of an n-ball.” Near the top of that page was the formula I sought:
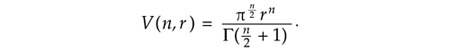
Later in this column I’ll say a few words about where this formula came from, both mathematically and historically, but for now I merely note that the only part of the formula that ventures beyond routine arithmetic is the gamma function, Γ, which is an elaboration on the idea of a factorial. For positive integers, Γ(n+1)=n!=1×2×3×...×n. But the gamma function, unlike the factorial, is also defined for numbers other than integers. For example, Γ(½) is equal to the square root of π.
When I discovered the n-ball formula, I did not pause to investigate its provenance or derivation. I was impatient to plug in some numbers and see what would come out. So I wrote a hasty one-line program in Mathematica and began tabulating the volume of a unit ball in various dimensions. I had definite expectations about the outcome. I believed that the volume of the unit ball would increase steadily with n, though at a lower rate than the volume of the enclosing s=2 cube, thereby confirming Bellman’s curse of dimensionality. Here are the first few results returned by the program:
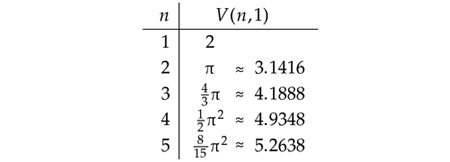
I noted immediately that the values for one, two and three dimensions agreed with the results I already knew. (This kind of confirmation is always reassuring when you run a program for the first time.) I also observed that the volume was slowly increasing with n, as I had expected.
But then I looked at the continuation of the table:

Beyond the fifth dimension, the volume of a unit n-ball decreases as n increases! I tried a few larger values of n, finding that V(20,1) is about 0.0258, and V(100,1) is in the neighborhood of 10–40. Thus it looked very much like the n-ball dwindles away to nothing as n approaches infinity.
I had thought that I understood Bellman’s curse: Both the n-ball and the n-cube grow along with n, but the cube expands faster. In fact, the curse is far more damning: At the same time the cube inflates exponentially, the ball shrinks to insignificance. In a space of 100 dimensions, the fraction of the cubic volume filled by the ball has declined to 1.8×10–70. This is far smaller than the volume of an atom in relation to the volume of the Earth. The ball in the box has all but vanished. If you were to select a trillion points at random from the interior of the cube, you’d have almost no chance of landing on even one point that is also inside the ball.
What makes this disappearing act so extraordinary is that the ball in question is still the largest one that could possibly be stuffed into the cube. We are not talking about a pea rattling around loose inside a refrigerator carton. The ball’s diameter is still equal to the side length of the cube. The surface of the ball touches every face of the cube. (A face of an n-cube is an (n–1)-cube.) The fit is snug; if the ball were made even a smidgen larger, it would bulge out of the cube on all sides. Nevertheless, in terms of volume measure, the ball is nearly crushed out of existence, like a black hole collapsing under its own mass.
How can we make sense of this seeming paradox? One way of understanding it is to acknowledge that the ball fills the middle of the cube, but the cube doesn’t have much of a middle; almost all of its volume is away from the center, huddling in the corners. A simple counting argument gives a clue to what’s going on. As noted above, the ball touches the enclosing cube at the center of each face, but it does not reach out into the corners. A 100-cube has just 200 faces, but it has 2100 corners.
Another approach to understanding the collapse of the n-ball is to imagine poking skewers through the cube along various diameters. (A diameter is any straight line that passes through the center point.) The shortest diameters run from the center of a face to the center of the opposite face. For the cube enclosing a unit ball, the length of this shortest diameter is 2, which is both the side length of the cube and the diameter of the ball. Thus a skewer on the shortest diameter lies inside the ball throughout its length.
The longest diameters of the cube extend from a corner through the center point to the opposite corner. For an n-cube with side length s=2, the length of this diameter is 2 times the square root of n. Thus in the 100-cube surrounding a unit ball, the longest diameter has length 20; only 10 percent of this length lies within the ball. Moreover, there are just 100 of the shortest diameters, but there are 299 of the longest ones.
Here is still another mind-bending trick with balls and boxes to suggest just how weird space becomes in higher dimensions. I learned of it from Barry Cipra, who published a description in Volume 1 of What’s Happening in the Mathematical Sciences (1991). On the plane, a square with sides of length 4 will accommodate four unit disks in a two-by-two array, with room for a smaller disk in the middle; the radius of that smaller disk is √2 – 1. In three dimensions the equivalent 3-cube fits eight unit balls, plus a smaller ninth ball in the middle, whose radius is √3 – 1. In the general case of n dimensions, the box has room for 2n unit n-balls in a rectilinear array, with one additional ball in the vacant central space, and the central ball has a radius of √n – 1. Look what happens when n reaches 9. The “smaller” central ball now has a radius of 2, which makes it twice the size of the 512 surrounding balls. Furthermore, the central ball has expanded to reach the sides of the bounding box, and will burst through the walls with any further increase in dimension.
I was taken by surprise when I learned that the volume of a unit n-ball goes to zero as n goes to infinity; I had expected the opposite. But something else surprised me even more—the fact that the volume function is not monotonic. Either a steady increase or a steady decrease seemed more plausible than having the volume grow for a while, then reach a peak at some finite value of n, and thereafter decline. This behavior singles out a particular dimension for special attention. What is it about five-dimensional space that allows a unit 5-ball to spread out more expansively than any other n-ball?
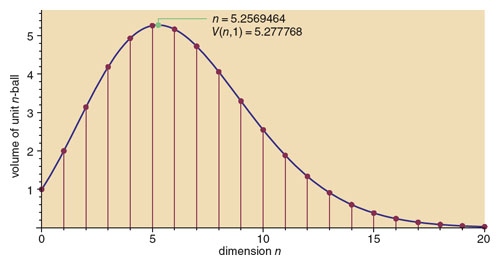
Illustration by Brian Hayes.
I can offer an answer, although it doesn’t really explain much. The answer is that everything depends on the value of π. Because π is a little more than 3, the volume peak comes in five dimensions; if π were equal to 17, say, the unit ball with maximum volume would be found in a space with 33 dimensions.
To see how π comes to have this role, we’ll have to return to the formula for n-ball volume. We can get a rough sense of the function’s behavior from a simplified version of the formula. In the first place, if we are interested only in the unit ball, then r is always equal to 1, and the rn term can be ignored. That leaves a power of π in the numerator and a gamma function in the denominator. If we consider only even values of n, so that n/2 is always an integer, we can replace the gamma function with a factorial. For brevity, let m=n/2; then all that remains of the formula is this ratio: πm/m!.
The simplified formula says that the n-ball volume is determined by a race between πm and m!. Initially, for the smallest values of m, πm sprints ahead; for example, at m=2 we have π2≈10, which is greater than 2!=2. In the long run, however, m! will surely win this race. Both πm and m! are products of m factors, but in πm the factors are all equal to π, whereas in m! they range from 1 up to m. Numerically, m! first exceeds πm when m=7, and thereafter the factorial grows very much larger.
This simplified analysis accounts for the major features of the volume curve, at least in a qualitative way. The volume of a unit ball has to go to zero in infinite-dimensional space because zero is the limit of the ratio πm/m!. In low dimensions, on the other hand, the ratio is increasing with m. And if it’s going uphill for small m and downhill for large m, there must be some intermediate value where the function reaches a maximum.
To get a quantitative fix on the location of maximum, we must return to the formula in its original form and consider odd as well as even numbers of dimensions. Indeed, we can take a step beyond mere integer dimensions. Because the gamma function is defined for all real numbers, we can treat dimension as a continuous variable and ask with finer resolution where the maximum volume occurs. A numerical solution to this calculus problem—found with further help from Mathematica—shows a peak in the volume curve at n≈5.2569464; at this point the unit ball has a volume of 5.2777680.
With a closely related formula, we can also calculate the surface area of an n-ball. Like the volume, this quantity reaches a peak and then falls away to zero. The maximum is at n≈7.2569464, or in other words two dimensions larger than the volume peak.
The arithmetic behind all these results is straightforward; attaching meaning to the numbers is not so easy. In particular, I can see numerically—by comparing powers of π with factorials—why the unit ball’s volume reaches a maximum at n=5. But I have no geometric intuition about five-dimensional space that would explain this fact. Perhaps readers with deeper vision will be able to provide some insight.
The results on noninteger dimensions are quite otherworldly. The notion of fractional dimensions is familiar enough, but it is generally applied to objects, not to spaces. For example, the Sierpinsky triangle, with its endlessly nested holes within holes, is assigned a dimension of 1.585, but the triangle is still drawn on a plane of dimension 2. What would it mean to construct a space with 5.2569464 mutually perpendicular coordinate axes? I can’t imagine—and that’s not just a figure of speech.
Another troubling question is whether it really makes sense to compare volumes across dimensions. Each dimension requires its own units of measure, and so the relative magnitudes of the numbers attached to those units don’t mean much. Is a disk of area 10 square centimeters larger or smaller than a ball of volume 5 cubic centimeters? We can’t answer; it’s like comparing apples and orange juice.
Nevertheless, I believe there is indeed a valid basis for making comparisons. In each dimension volume is to be measured in terms of a standard volume in that dimension. The obvious standard is the unit cube (sometimes called the “measure polytope”), which has a volume of 1 in all dimensions. Starting at n=1, the unit ball is larger than the unit cube, and the ball-to-cube ratio gets still larger through n=5; then the trend reverses, and eventually the ball is much smaller than the unit cube. This changing ratio of ball volume to cube volume is the phenomenon to be explained.
The volume formulas I learned as a child were incantations to be memorized rather than understood. I would like to do better now. Although I cannot give a full derivation of the n-ball formula—for lack of both space and mathematical acumen—perhaps the following remarks will shed some light.
The key idea is that an n-ball has within it an infinity of (n–1)-balls. For example, a series of parallel slices through the body of an onion turns a 3-ball into a stack of 2-balls. Another set of cuts, perpendicular to the first series, reduces each disklike slice to a collection of 1-balls—linear ribbons of onion. If you go on to dice the ribbons, you have a heap of 0-balls. (With real onions and knives these operations only approximate the forms of true n-balls, but the methods work perfectly in the mathematical kitchen.)
This decomposition suggests a recursive algorithm for computing the volume of an n-ball: Slice it into many (n–1)-balls and sum up the volumes of the slices. How do you compute the volumes of the slices? Apply the same method, cutting the (n–1)-balls into (n–2)-balls. Eventually the recursion bottoms out at n=1 or n=0, where the answers are known. (The volume of a 1-ball is 2r; the 0-ball is assigned a volume of 1.) Letting the thickness of the slices go to zero turns the sum into an integral and leads to an exact result.
In practice, it’s convenient to use a slightly different recursion with a step size of 2. That is, the volume of an n-ball is computed from that of an (n–2)-ball. The specific rule is: Given the volume of an (n–2)-ball, multiply by 2πr2/n to get the volume of the corresponding n-ball. (Showing why the multiplicative factor takes this particular form is the hard part of the derivation, which I am going to gingerly avoid; it requires an exercise in multivariable calculus that lies beyond my abilities.)
The procedure is easy to express in the form of a computer program:
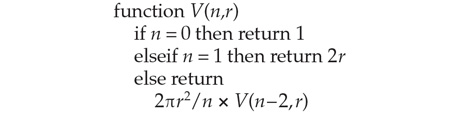
For even n, the sequence of operations carried out by this program amounts to:
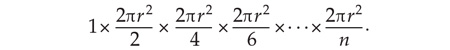
For odd n, the result is instead the product of these terms:
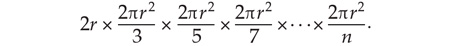
For all integer values of n the program yields the same output as the formula based on the gamma function.
A question I cannot answer with certainty is who first wrote down the n-ball formula. I have paddled up a long river of references, but I’m not sure I have reached the true source.
My journey began with the number 5.2569464. I entered the digits into the On-Line Encyclopedia of Integer Sequences, the vast compendium of number lore created by Neil J. A. Sloane. I found what I was looking for in sequence A074455. A reference there directed me to Sphere Packings, Lattices, and Groups, by John Horton Conway and Sloane. That book in turn cited An Introduction to the Geometry of N Dimensions, by Duncan Sommerville, published in 1929. The Sommerville book devotes a few pages to the n-ball formula and has a table of values for dimensions 1 through 7, but it says little about origins. However, further rooting in library catalogs revealed that Sommerville—a Scottish mathematician who emigrated to New Zealand in 1915—also published a bibliography of non-Euclidean and n-dimensional geometry.
The bibliography lists five works on “hypersphere volume and surface”; the earliest is a problem and solution published in 1866 by William Kingdon Clifford, a brilliant English geometer who died young. Clifford’s derivation of the formula is clearly original work, but it was not the first.
Elsewhere Sommerville mentions the Swiss mathematician Ludwig Schläfli as a pioneer of n-dimensional geometry. Schläfli’s treatise on the subject, written in the early 1850s, was not published in full until 1901, but an excerpt translated into English by Arthur Cayley appeared in 1858. The first paragraph of that excerpt gives the volume formula for an n-ball, commenting that it was determined “long ago.” An asterisk leads to a footnote citing papers published in 1839 and 1841 by the Belgian mathematician Eugène Catalan.
Looking up Catalan’s articles, I found that neither of them gives the correct formula in full, although they’re close. Catalan deserves partial credit.
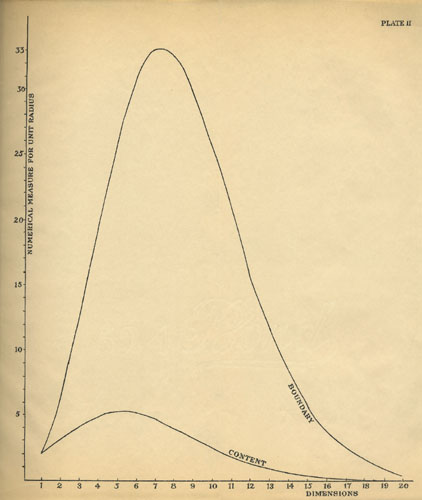
Not one of these early works pauses to comment on the implications of the formula—the peak at n=5 or the trend toward zero volume in high dimensions. Of the works mentioned by Sommerville, the only one to make these connections is a thesis by Paul Renno Heyl, published by the University of Pennsylvania in 1897. This looked like a fairly obscure item, but with help from Harvard librarians, the volume was found on a basement shelf. I later discovered that the full text (but not the plates) is available on Google Books.
Heyl was a graduate student at the time of this work. He went on to a career with the National Bureau of Standards, and he was also a writer on science, philosophy and religion. (His best-known book was The Mystery of Evil.)
In the 1897 thesis Heyl derives formulas for both volume and surface area (which he calls “content” and “boundary”), and gives a lucid account of multidimensional geometry in general. He clearly appreciates the strangeness of the discovery that “… in a space of infinite dimension our locus can have no content at all.” I will allow Heyl to have the last word on the subject:
We might be pardoned for supposing that in a space of infinite dimension we should find the Absolute and Unconditioned if anywhere, but we have reached an opposite conclusion. This is the most curious thing I know of in the Wonderland of Higher Space.
©Brian Hayes
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.