Slicing a Cone for Art and Science
By Daniel S. Silver
Albrecht Dürer searched for beauty with mathematics.
Albrecht Dürer searched for beauty with mathematics.

DOI: 10.1511/2012.98.408
Albrecht Dürer (1471–1528), master painter and printmaker of the German Renaissance, never thought of himself as a mathematician. Yet he used geometry to uncover nature’s hidden formulas for beauty. His efforts influenced renowned mathematicians, including Gerolamo Cardano and Niccolo Tartaglia, as well as famous scientists such as Galileo Galilei and Johannes Kepler.

Wikimedia Commons
We praise Leonardo da Vinci and other Renaissance figures for embracing art and science as a unity. But for artists such as da Vinci and Dürer, there was little science to embrace. Efforts to draw or paint directly from nature required an understanding of physiology and optics that were not found in the ancient writings of Galen or Aristotle. It was not just curiosity but also need that motivated Dürer and his fellow Renaissance artists to initiate scientifc investigations.
Dürer’s nature can seem contradictory. Although steadfastly religious, he sought answers in mathematics. He was outwardly modest but inwardly vain. He fretted about money and forgeries of his work, yet to others he appeared to be a simple man, ready to help fellow artists.
Concern for young artists motivated Dürer to write an ambitious handbook for all disciplines of artists. It has the honor of being the first serious mathematics book written in the German language. Its title, Underweysung der Messung, might be translated as A Manual of Measurement. Walter Strauss, who translated Dürer’s work into English, gave the volume a pithy and convenient moniker: the Painter’s Manual.
Dürer begins his extraordinary manual with apologetic words, an inversion of the famous warning of Plato’s Academy: Let no one untrained in geometry enter here:
The most sagacious of men, Euclid, has assembled the foundation of geometry. Those who understand him well can dispense with what follows here, because it is written for the young and for those who lack a devoted instructor.
The manual was organized into four books and printed in Nüremberg in 1525, just three years before the artist’s death. It opens with the definition of a line, and it closes with a discussion of elaborate mechanical devices for accurate drawing in perspective. In between can be found descriptions of spirals, conchoids and other exotic curves. Constructions of regular polygons are given. Cut-out models (“nets”) of polyhedra are found. There is also an important section on typography, containing a modular construction of the Gothic alphabet. An artist who wishes to draw a bishop’s crozier will learn how to do it with a compass and ruler. An architect who wants to erect a monument might find some sort of inspiration in Dürer’s memorial to a drunkard, a humorous design complete with coffin, beer barrel and oversized drinking mug.
Scholarly books of the day were generally written in Latin. Dürer wrote Underweysung der Messung in his native language because he wanted it to be accessible to all German readers, especially those with limited formal education. But there was another reason: Dürer’s knowledge of Latin was rudimentary. Others later translated Underweysung der Messung into several different languages, including Latin.
There was no reason to expect that Dürer should have been fluent in Latin. As the son of a goldsmith, he was lucky to have gone to school at all. Fortunately for the world, Dürer displayed his unusual intelligence at an early age. “My father had especial pleasure in me, because he said that I was diligent in trying to learn,” he recalled. He was sent to school, possibly the nearby St. Sebald parochial school, where he learned to read and write. He and his fellow students carried slates or wax writing tablets to class. (Johannes Gutenberg had invented a printing press only 40 years before, and books were still a luxury.) Learning was a slow, oral process.
When Dürer turned 13, he was plucked from school so that he could begin learning his father’s trade. At that age, he produced a self-portrait that gives a hint of his emerging artistic skill. Self-portraits at the time were rare. Dürer produced at least 11 more during his lifetime.
What might have inspired a tradesman’s son to study the newly rediscovered works of ancient Greek mathematicians such as Euclid and Apollonius? Part of the answer can be found in the intellectual atmosphere of Nüremberg at the time. In 1470, Anton Koberger founded the city’s first printing house. One year later, he became Dürer’s godfather. Science and technology were so appreciated in Nüremberg that the esteemed astronomer Johannes Müller von Königsberg, also known as Regiomontanus (1436–1476), settled there and built an observatory.
The rest of the answer can be found in the dedication of the Painter’s Manual: “To my especially dear master and friend, Herr Wilbolden Pirckheymer, I, Albert Dürer wish health and happiness.” This master, whose name is more commonly spelled Willibald Pirckheimer (1470–1530), was a scion of one of Nüremberg’s most wealthy and powerful families. He was enormous in many ways, both physically and in personality, as well as boastful and argumentative. He was also a deeply knowledgeable humanist with a priceless library.
Pirckheimer’s house was a gathering place for Nüremberg’s brilliant minds. Despite the wide difference between their social rankings, Dürer and Pirckheimer became lifelong friends. Pirckheimer depended on Dürer to act as a purchasing agent during his travels, scouting for gems and other valuable items. Dürer depended on Pirckheimer for access to rare books and translation from Greek and Latin.
The word “Messung” meant more to Dürer than simple measurement. “Harmony” might have been closer to the mark. In his youth, possibly in 1494, Dürer had marveled over a geometrically based drawing of male and female figures by the Venetian artist Jacopo de’ Barbari (about 1440–1516). Despite the fact that de’ Barbari was unwilling to share his methods—or maybe because of it—Dürer became convinced that the secrets of beauty might be found by means of mathematics. Dürer was only 23 years old at the time. He devoted the remaining three decades of his life to the search, for as he reflected some years later, “I would rather have known what [de’ Barbari’s] opinions were than to have seen a new kingdom.” Geometry, recovered from ancient works, lit his way.

Wikimedia Commons
The gravity of Dürer’s quest can be sensed in his enigmatic engraving Melencolia I. Now approaching the 500th anniversary of its creation, Melencolia I has been the subject of more academic debate than any other print in history. Is the winged figure dejected because she has tried but failed to discover beauty’s secret? She holds in her hand an open compass. Above her head is a magic square, the first to be seen in Western art. (In a magic square, the numbers in each row and column, as well as the two main diagonals, add to the same total, in this case 34. In this one, the date of the engraving, 1514, appears in the lowest row.) Clearly Dürer’s mathematical interests were not limited to geometry.
When he wrote the Painter’s Manual, Dürer was approaching the end of a successful career. As a young man eager to learn more about the new science of perspective and to escape outbreaks of plague at home, he had made two trips to Italy. After the first journey, his productivity soared. Dürer’s self-portrait of 1498 radiates an expanding confidence. (It was not the first time that plague encouraged scientific discovery, nor was it the last. In 1666 Isaac Newton escaped an outbreak of plague at Cambridge University, returning to his mother’s farm, where he had the most profitable year that science has ever known.)
During his second visit to Italy, Dürer met with fellow artists including the great master Giovanni Bellini, who praised his work. Dürer came to the conclusion that German artists could rise to the heights of the Italians, but only if they learned the foundations of their art. Such a foundation would prevent mistakes—and such a foundation required geometry. He returned with an edition of Euclid that bears his inscription: “I bought this book at Venice for one ducat in the year 1507—Albrecht Dürer.”
Dürer purchased a house in Nüremberg and began to study mathematics. The Painter’s Manual was not the book that he had originally planned to write. He had started work on Vier Bücher von Menschlicher Proportion (“Four Books on Human Proportion”), but soon realized that the mathematical demands that it placed on young readers were too great. The Painter’s Manual was intended as a primer.
Work on the Painter’s Manual, too, was temporarily halted when, in 1523, Dürer acquired 10 books from the library of Nüremberg mathematician Bernhard Walther (1430–1504). Walther had been a student of Regiomontanus and had acquired important books and papers from him. But Walther was a moody man who denied others access to this valuable cache. Walther died, but his library remained with his executors for two decades. Finally its contents had been released for sale. Dürer’s precious purchases were chosen and appraised by Pirckheimer. It took Dürer two more years to absorb the ideas these books contained. The completion of the Painter’s Manual would just have to wait.
It would be a book for artists, or so Dürer thought. Nevertheless he allowed himself to be carried aloft by mathematics. “How is it that two lines which meet at an acute angle which is made increasingly smaller will nevertheless never join together, even at infinity?” he asks (and proceeds to give a strange explanation). Later he writes: “If you wish to construct a square of the same area as a triangle with unequal sides, proceed as follows.” It is difficult to imagine any artist of the 16th century making use of such ideas. These are the thoughts of a compulsive theoretician.
Time for Dürer to complete his Painter’s Manual was running out. In December 1520, he had foolishly trekked to the swamps of Zeeland in the southwestern Netherlands, hoping to inspect a whale that had washed ashore. Alas, the whale had already washed away by the time he arrived. It was not a healthy place to visit, and the chronic illness that he contracted there eventually killed him after eight painful years.

Wikimedia Commons
Dürer’s self-portrait of 1522 contrasts disturbingly with his earlier one. In the words of Strauss: “It represents Dürer himself in the nude, with thinned, disheveled hair and drooping shoulders, his body ravaged by his lingering disease.” He fashioned himself as the Man of Sorrows.
“The subject [Conic Sections] is one of those which seem worthy of study for their own sake.” —Apollonius of Perga
Although there is much in the Painter’s Manual that rewards close examination, one specific area worthy of concentration is Dürer’s treatment of conic sections. The techniques that Dürer found to draw them anticipate the field of descriptive geometry that Gaspard Monge (1746–1818) developed later. The curves themselves would accompany a revolution in astronomy.
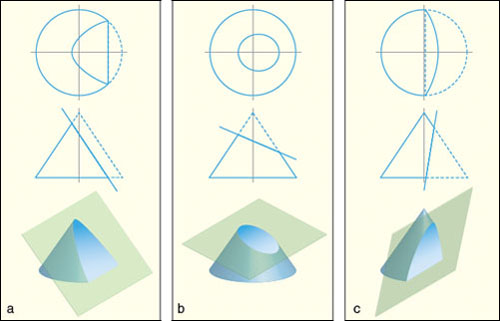
Illustration by Barbara Aulicino.
“The ancients have shown that one can cut a cone in three ways and arrive at three differently shaped sections,” Dürer writes toward the end of Book I. “I want to teach you how to draw them.”
Menaechmus (circa 350 B.C.), who knew Plato and tutored Alexander the Great, is thought to have discovered conic sections (often called simply “conics”). He found them while trying to solve the famous Delian problem of “doubling the cube.” According to legend, terrified citizens of the Greek island of Delos were reassured by an oracle that plague would depart only after they had doubled the size of Apollo’s cubical altar. Assuming that the altar had unit volume, the task of doubling it amounted to constructing a new edge of length precisely equal to the cube root of 2. Although the legend is doubtful, the Delian problem was certainly studied in Plato’s Academy. Plato insisted on an exact solution accomplished using only ruler and compass.
Ingenious ruler-and-compass constructions abound in the Painter’s Manual. Dürer’s construction of a regular pentagon is particularly noteworthy. The construction was due not to Euclid but rather to one that had been taught by Ptolemy and is found in his Almagest.
In 1837, the French mathematician Pierre Wantzel (1814–1848) proved that doubling the cube with ruler and compass is impossible. However, Menaechmus changed the rules of the game and managed to win. By intersecting a right-angled cone with a plane perpendicular to its side, he produced a curve that was later called a parabola. Then by intersecting two parabolas, chosen carefully, Menaechmus produced a line segment of length equal to the cube root of 2. (The parabola can be described by a simple equation x = py2. The positive number p, called the latus rectum, is a parameter that uniquely describes the shape.)
Menaechmus looked at other sorts of cones. When the cone’s angle was either less than or greater than 90 degrees, two new types of curves resulted from their intersection with a plane. A century later, Apollonius of Perga (262–190 B.C.) called the three curves parabola, ellipse and hyperbola, choosing Greek words meaning, respectively: comparison, fall short and excess. Echoes are heard today in the English words such as parable, ellipsis and hyperbole.
Today there is debate as to whether the terms originated with Apollonius. In any event, they were likely adapted from earlier terminology of Pythagoras (570–circa 495 B.C.) concerning a construction known as “application of areas.” The interpretation in terms of angle is historically inaccurate but mathematically equivalent and simpler to state.
Apollonius’s accomplishments went beyond nomenclature. He made a discovery that afforded a lovely simplification. Instead of employing three different types of cones, as Menaechmus did, Apollonius used a single cone. Then by allowing the plane to slice the cone at different angles, he produced all three conics.
Associated with an ellipse or hyperbola are a pair of special points called foci. (For a circle, a special case of an ellipse, the distance between the two foci is zero.) Distances to the foci determine the curves in a simple way: The ellipse consists of those points such that the sum of distances to the foci is constant. Likewise, the hyperbola consists of points such that the difference is a constant.
Tilt a glass of water toward you and observe the shape of the water’s edge. It is an ellipse. So is the retinal image of a circle viewed from a generic vantage point.
Johannes Kepler (1571–1630) made the profound discovery that the orbit of Mars is an ellipse with the Sun at one focus. Kepler introduced the word “focus” into the mathematics lexicon in 1604. It is a Latin word meaning hearth or fireplace. What word could be more appropriate for the location of the Sun?
Kepler’s letter to fellow astronomer David Fabricius (1564–1617), dated October 11, 1605, reveals that Kepler had read Dürer’s description of conics:
So, Fabricius, I already have this: That the most true path of the planet [Mars] is an ellipse, which Dürer also calls an oval, or certainly so close to an ellipse that the difference is insensible.
In fact, Dürer used a more flavorful term for an ellipse, as we will see.
Nature’s parabolas and hyperbolas are less apparent than the ellipse. A waterspout and the path of a cannonball have parabolic trajectories. The wake generated by a boat can assume the form of a hyperbola, but establishing that fact requires more mathematics—or a boat.
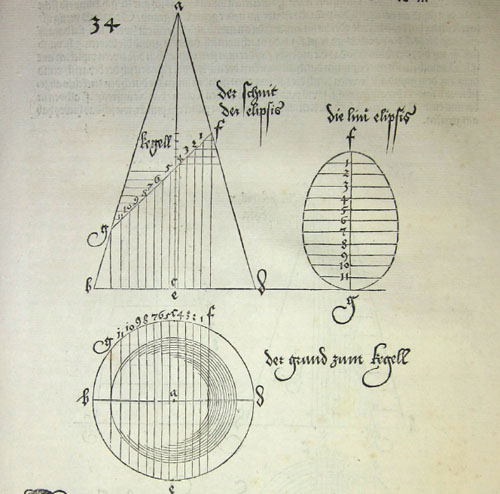
The significance of Dürer’s treatment of conics is the technique that he used for drawing them, a fertile method of parallel projection. Art historian Erwin Panofsky observed that the technique was “familiar to every architect and carpenter but never before applied to the solution of a purely mathematical problem.” In brief, Dürer viewed a cut cone from above as well as from the side, then projected downward. His trick was to superimpose the two views and then transfer appropriate measurements using dividers. In this way he relocated the curve from the cone to a two-dimensional sheet of paper.
IPhotograph courtesy of the author.
Dürer’s method was correct, but the master draftsman blundered while transferring measurements. He mistakenly believed that the ellipse was wider at the bottom of the cone than at the top, an understandable error considering the shape of the cone. As he transferred the distances with his divider, his erroneous intuition took hold of his hand.
Dürer writes: “The ellipse I call eyer linie [egg line] because it looks like an egg.” Egg lines for ellipses can indeed be spotted in Dürer’s work, such as in the bell in Melencolia I. Dürer knew no German equivalent of the Greek word “ellipse.” The appellation he concocted drew attention to his error, and the egg line persisted in German works for nearly a century.

Image courtesy of Linda Hall Library of Science, Engineering & Technology.
It is easy to understand why Kepler had an interest in Dürer’s flawed analysis of the ellipse. For 10 years beginning in 1601, Kepler struggled to understand the orbit of Mars, a problem that had defeated Regiomontanus. Until he understood that the orbit was an ellipse, Kepler believed that it was some sort of oval. In fact, he specifically used the word “oval,” a descendant of the Latin word “ovum” meaning egg.
Kepler was not the first to believe that a planet’s orbit might be egg-shaped. Georg von Peuerbach (1423–1461), a teacher of Regiomontanus, had said as much in Theoricae novae planetarum. Published in Nüremberg in 1473 and reprinted 56 times, Peuerbach’s treatise influenced both Copernicus and Kepler. The 1553 edition, published by Erasmus Reinhold (1511–1553), a pupil of Copernicus, included a comment about Mercury’s orbit that might have caused Kepler to go back to the Painter’s Manual:
Mercury’s [orbit] is egg-shaped, the big end lying toward his apogee, and the little end towards its perigee.
Later Kepler had this to say about the orbit of Mars:
The planet’s orbit is not a circle but [beginning at the aphelion] it curves inward little by little and then [returns] to the amplitude of a circle at [perihelion]. An orbit like this is called an oval.
It is a safe bet that few artists in 16th-century Germany felt the need to draw a parabola. In what seems like a marketing effort, Dürer tells his readers how it can be fashioned into a weapon of mass destruction.
The story that Archimedes set fire to an invading Roman fleet during the siege of Syracuse was well known in Dürer’s time. Dioclese, a contemporary of Archimedes, explained the principle in his book On Burning Mirrors, preserved by Muslims in the 9th century.
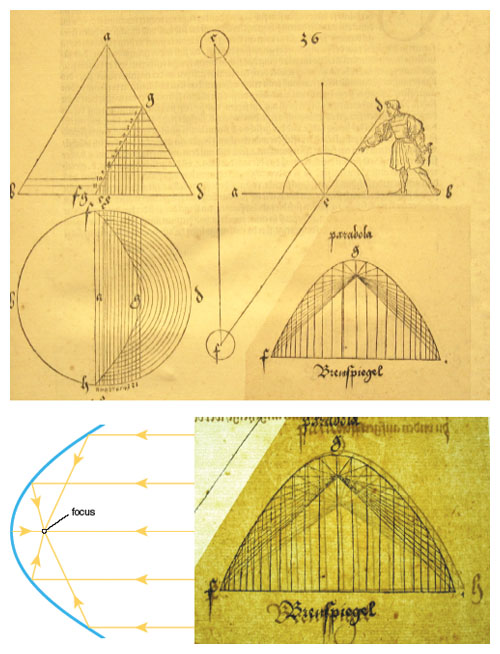
Dioclese had observed something special about the parabola that had escaped the notice of Apollonius: On its axis of symmetry there is a point—a single focus—with the property that if a line parallel to the axis reflects from the parabola with the same angle with which it strikes, the reflected line will pass through the focus. In physical terms, a mirror in the shape of a paraboloid, a parabola revolved about its axis, will gather all incoming light at the focus. Collect enough light, and whatever is at the focus will become hot.
Making an effective burning mirror is not a simple matter. Unless the parabola used is sufficiently wide, the mirror will not collect enough light. Dürer writes:
If you plan to construct a burning mirror of paraboloid shape, the height of the cone you have to use should not exceed the diameter of the base—or this cone should be of the shape of an equilateral triangle.
Photographs courtesy of the author.
Dürer goes on to explain why the angle of incidence of a light beam striking a mirror is equal to the angle of reflection. An elegant drawing of an artisan (possibly the artist) holding a pair of dividers does little to help matters. Dürer probably sensed that he was getting into a rough technical patch. He concludes the section desperately:
The cause of this has been explained by mathematicians. Whoever wants to know it can look it up in their writings. But I have drawn my explanation . . . in the figure below.
Burning mirrors might have sounded useful to readers of the Painter’s Manual. The first scientific evidence that Archimedes’s mirrors might not have been such a hot idea had to wait for 12 years until René Descartes expressed doubts in his treatise Dioptrique. Nevertheless, since the time of Archimedes, burning mirrors, whatever their effectiveness, were constructed in a more practical, approximate fashion with sections of a sphere. (In 1668, Isaac Newton designed the first reflecting telescope on the principle of the burning mirror, with an eyepiece near the focus. He substituted a spherical mirror to simplify its construction.) It seems that Dürer liked parabolas and was determined to write about them.
Dürer invented German names for the parabola and the hyperbola as well as the ellipse. The parabola he called a Brenn Linie (“burn line”). “And the hyperbola I shall call gabellinie [fork line],” he writes, but he offers no explanation for his choice. Nor, it seems, has a reason been suggested by anyone else. Dürer might have been paying tribute to the many gabled houses of which Nüremberg was proud, the artist’s own home near the Thiergärtnerthor included. In the Painter’s Manual, Dürer constructs the hyperbola but has little to say about it.
Much of what Dürer knew about conic sections came from Johannes Werner (1468–1522). A former student of Regiomontanus, Werner was an accomplished instrument maker. He made contributions to geography, meteorology and mathematics. A lunar impact crater named in his honor is not far from a crater named Regiomontanus.
Werner’s Libellus super viginti duobus elementis conicis was published in 1522, at the time when Dürer was studying conics. The volume’s 22 theorems were intended to introduce the author’s work on the Delian problem. From handwritten notes, it appears that Werner died during his book’s printing. (Werner’s book soon became very rare. It is reported that the Danish astronomer Tycho Brahe could not find a copy for sale anywhere in Germany.)
Since 1508, Werner had been serving as priest at the Church of St. John, not far from Dürer’s house. Like Pirckheimer, Werner acquired some of the rare books and papers that had been in Walther’s possession. However, Werner knew no Greek and probably relied on Pirckheimer for translation. (His commentary on Ptolemy, published in 1514, is dedicated to Pirckheimer.) Like Dürer, Werner would have been a frequent visitor to Pirckheimer’s house.
Photographs courtesy of the author.
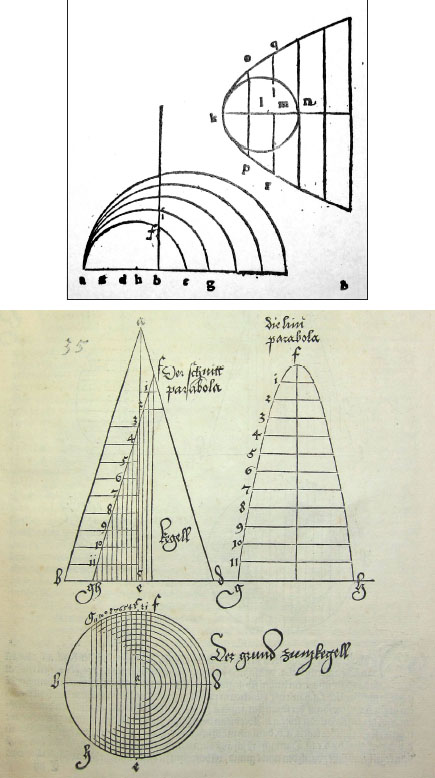
I believe that Dürer was inspired by Werner’s novel construction of the parabola. The cone that he used was an oblique cone with vertex directly above a point on the base circle. A cut by a vertical plane produced the parabola. Regularly spaced, circular cross-sections of the cone are in the lower diagram, each tangent to a point that lies directly below the vertex of the cone. The cutting plane is seen in profile as a line through points labeled b and f. By transferring the segments cut by the circles along the line, Werner produced the semi-arcs transverse to the line through k and n in the upper figure.
Had Dürer seen the picture, which is likely, Germany’s master of perspective would have had no trouble imagining the tangent circles stacked in three dimensions, the smallest coming closest to his eye. The method of parallel projections that is often credited to Dürer might well have derived from Werner’s construction.
In Appendix Duodecima of his book, Werner explains the reflective properties of the parabola to his audience. He also tells the reader how to locate the focus: Its distance from the vertex is one quarter of the length of the segment ab. (The length of ab, which is equal to the length of kn, is the latus rectum of the parabola—the distance between the slicing plane and the vertex of the cone.)
But Dürer used a right cone with vertex directly above the center of the circular base, so his cross-sectional circles became concentric rather than tangent to a single point as in Werner’s diagram.
Unfortunately for Dürer, Werner’s formula for the location of the focus no longer applied. Whether Dürer computed the distance incorrectly or merely guessed, we do not know. However, in every copy of the 1525 publication a small piece of paper with the correct drawing had to be pasted by hand over the erroneous one. By holding the final product up to the light, Dürer’s mistake is revealed.
For Albrecht Dürer, questions of technique eventually gave way to those of philosophy. In 1523, he wondered at the way “one man may sketch something with his pen on half a sheet of paper in one day . . . and it turns out to be better and more artistic than another’s big work at which its author labors with the utmost diligence for a whole year.”
The belief that divine genius borrows the body of a fortunate artist was common in Dürer’s time. According to Panofsky, Leonardo da Vinci would have been perplexed had someone called him a genius. But Dürer had begun to see the creative process differently. For him, it became one of synthesis governed by trained intuition.
Dürer’s last name was likely derived from the German word tür, meaning door. (His father was born in the Hungarian town of Ajtas, which is related to the Hungarian word for door, ajitó.)

Scala/Art Resource, NY
It is a fitting name for someone who opened a two-way passage between mathematics and art. As Panofsky observed: “While [the Painter’s Manual] familiarized the coopers and cabinetmakers with Euclid and Ptolemy, it also familiarized the professional mathematicians with what may be called ‘workshop geometry.’ ”
Dürer used geometry to search for beauty, but he never regarded mathematics as a substitute for aesthetic vision. It was a tool to help the artist avoid errors. However, the Painter’s Manual demonstrates that mathematics and, in particular, geometry, meant much more to him. Four centuries after its publication, poet Edna St. Vincent Millay wrote: “Euclid alone has looked on Beauty bare.” Dürer might have agreed.
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.