This Article From Issue
May-June 2010
Volume 98, Number 3
Page 256
DOI: 10.1511/2010.84.256
ISAAC NEWTON ON MATHEMATICAL CERTAINTY AND METHOD. Niccolò Guicciardini. xxvi + 422 pages. The MIT Press, 2009. $55.
Both the life and the work of Isaac Newton have been studied from such a variety of perspectives that one might wonder whether anything remains to be said about either. Newton’s epoch-making achievements in The Mathematical Principles of Natural Philosophy (Principia, 1687) are well known to educated readers, as is his role in the discovery of the calculus and his dispute with Gottfried Leibniz over who first invented it. Less familiar, at least to those who are not professional mathematicians, are the ways in which the mathematical tools that Newton had at his disposal tied in with his scientific, mathematical, foundational and more general philosophical aims. Many such tools were of his own invention, and he often kept their inner workings to himself or revealed them only to his acolytes. These tools and the variety of purposes they served are the subject of Niccolò Guicciardini’s wonderful new book, Isaac Newton on Mathematical Certainty and Method. Guicciardini, one of the most influential scholars of Newtonian mathematics and of mathematical physics and its development in the 18th century, offers an original and scholarly reconstruction of Newton’s mathematics and of his conception of mathematical methodology. He also explains the role that Newton envisioned mathematics should play in injecting certainty into natural philosophy.
But what is Newton’s mathematics? What is mathematical method? And why was there a need to inject certainty into natural philosophy? The answers to these questions take us on a long journey that covers, in 17 chapters, all the major aspects of Newton’s work and activities in the aforementioned areas. In the process, we are treated to a private visit to a place that is rarely accessible—the mathematician’s laboratory (in this case Newton’s).
By the time Newton began his mathematical studies in the early 1660s, mathematicians had already burst open the boundaries of ancient mathematics in two major directions. New indivisibilist and infinitesimalist techniques developed by Bonaventura Cavalieri, Evangelista Torricelli, John Wallis, James Gregory and others led to work with infinite series and other infinitary objects and techniques. The algebraization of mathematics was under way as well; having taken its start with François Viète and René Descartes, it would eventually come to define what “modern” mathematics is about. This does not mean, however, that the approach to mathematics found in the main texts of the Greek tradition (those of Euclid, Archimedes, Apollonius and Pappus, among others) was replaced by the new developments. The ancients were studied carefully, and some, including Newton, saw them as embodying the paradigm of correct methodology. Newton is characterized by Guicciardini as being in this sense an antimodernist.
Lest the reader be misled by this characterization, let us quickly review the major events in Newton’s mathematical career. In his early studies, Newton quickly became acquainted with the symbolic approach to geometry advanced in Descartes’ Géométrie (1637) and with the bold arithmetico-algebraic infinitary techniques championed by Wallis in Arithmetica Infinitorum (1656). By the mid-1660s, Newton was already producing pathbreaking results on binomial series and on infinite series applied to problems of quadratures (that is, the determination of areas), and he had already discovered what we now call the calculus, namely his method of fluxions. In the early 1670s he wrote the Optical Lectures, bringing to the fore the issue of the role of geometry in natural philosophy.
It was in the 1670s that Newton began to study the classics of ancient mathematics in depth. This led him to several results in projective geometry. One of his major achievements in this area was the classification of all cubic curves into five projective classes. But, concomitantly, he also developed an anti-Cartesian approach to mathematical methodology (in his manuscript titled “Errores Cartesij Geometriae,” for instance), which would characterize his stand on methodological issues from that moment on. This anti-Cartesian stand is evident in works such as the treatise “Geometria Curvilinea” (composed probably in the 1680s), which also reveals the influence of the work of Christiaan Huygens, another mathematician greatly indebted to the style of ancient mathematics.
But these methodological choices did not mean that Newton had removed from his toolbox the algebraic/analytic instruments. On the contrary, he had at his disposal and continued to develop techniques for solving mathematical problems that ranged from infinite series determinations, to projective studies in the style of the ancients, to algebraic techniques. As Guicciardini puts it,
it is often the case that in tackling a problem Newton made recourse to a baroque repertoire of methods: one encounters in the same folio algebraic equations, geometrical infinitesimals, infinite series, diagrams constructed according to Euclidean techniques, insights in projective geometry, quadratures techniques equivalent to sophisticated integrations, curves traced via mechanical instruments, numerical approximations.
From this point of view, it is quite interesting that Principia contains several unproved results on quadratures, which are key to some of its central theorems—results that Newton could only prove with algebraic/analytic machinery and which were inaccessible to him using only techniques that the ancient tradition would have approved of. This led to a certain tension, ultimately not resolved, between his mathematical practice and his preferred methodology. Among the works that followed the publication of Principia is the classification of cubic curves, which Newton obtained in the 1690s but only published in 1704, as an appendix to Opticks.
Guicciardini covers all of this and more in the six main parts that make up the book. Part 1 provides a general schema of Newton on mathematical method, part 2 details his work on algebra, part 3 covers the fluxional calculus, part 4 is devoted to Newton’s application of mathematics in natural philosophy, part 5 analyzes the geometrical investigations, and part 6 treats the philosophical and methodological issues that emerged in the priority dispute with Leibniz.
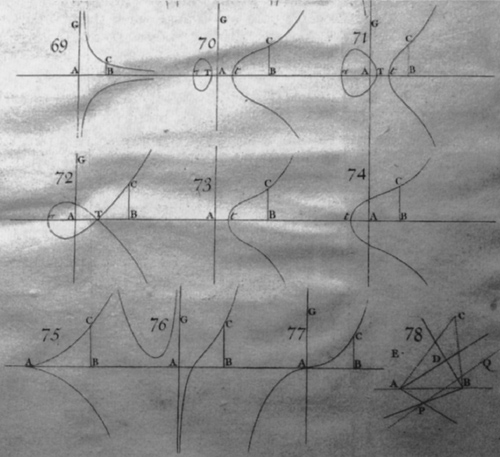
From Isaac Newton on Mathematical Certainty and Method.
I don’t have space to explain the mathematics in detail, but let me at least indicate what the main mathematical and methodological issues were that led to Newton’s anti-Cartesianism and antimodernism in mathematics. Descartes had limited the realm of geometry to what he called geometrical curves, essentially those that can be expressed by an algebraic equation (for instance the conic sections). He dubbed the curves that could not be expressed by such an equation “mechanical” and excluded them from geometry. By contrast, Newton wanted to include these curves in the realm of geometry and had a unified kinematic conception of curves that allowed him to treat with the same techniques problems such as the determination of tangents to conics (geometrical curves in Descartes’ sense) and the spiral or the quadratrix (which were mechanical curves, according to Descartes). This contrast also reveals a deeper divide between Cartesian mathematical practice and Newtonian practice. Descartes is a finitist at heart—in the Géométrie he does not accept infinitary procedures of any kind—but Newton makes use of all kinds of infinitary assumptions and reasoning.
Another major divide between Descartes and Newton—and here we come to the core of Newton’s antimodernism—consists in how to evaluate the role of algebra in geometry. What Descartes had achieved in the Géométrie was to show how certain geometrical problems could be stated by means of algebra. Stated in this way, a geometrical problem could then be transformed into an equivalent one calling for the solution(s) of a certain algebraic equation. But even for Descartes, reaching the algebraic equation was not the end of the story. With the algebraic equation in hand, what he required was a geometrical construction of the roots of the equation. The process leading to the setting up of an equation is one of algebraic analysis; the process yielding the construction of the roots is one of synthesis. However, the algebraic analysis soon loses view of the underlying geometrical nature of the problem, so that even when the roots of the equation are constructed geometrically, one is often left with no geometrical insight as to the nature of the problem. By contrast, Newton wanted to achieve solutions in which the geometrical analysis gives “elegant” and insightful access to the nature of the problem, followed by a synthetic (geometric) construction of the problem.
Newton was convinced that only geometrical (as opposed to algebraic) proofs can be considered certain, and indeed he recast even the mathematics of Principia in geometrical garb (using the synthetic method of fluxions). Favoring geometrical techniques was part and parcel of his ideal of injecting certainty into natural philosophy; in this he saw himself in opposition to the “skeptical probabilistic” attitude of many members of the Royal Society (such as Robert Hooke and Robert Boyle).
How exactly this concept of certainty is to be understood (and whether certainty means the same thing in natural philosophy as in pure geometry) is never actually spelled out by Newton (or by Guicciardini). But geometrical proofs have other epistemic virtues that make them superior to algebraic proofs. Newton says that they are “elegant” and “simple.” In particular, he uses the simplicity he attributes to geometrical proofs as evidence against the algebraic criteria of simplicity proposed by Descartes. It is exactly the emphasis on these methodological aspects of proofs (as opposed to the more traditional concerns with certainty and rigor, which are not the real focus of Newton’s attention) that make Newton’s methodological pronouncement of the highest interest, not only from a historical point of view but also from the point of view of that direction in contemporary philosophy of mathematics that emphasizes the analysis of epistemic nonfoundational issues in mathematical practice.
Guicciardini has done a splendid job of bringing out all of these fascinating aspects of Newton’s methodological reflections while presenting the reader with a great selection of examples of Newton’s mathematical practice. This book will become a classic. I recommend it very highly to any reader with interests in the history of mathematics, the history of science, or the philosophical issues emerging from mathematical and scientific practice.
Paolo Mancosu is a professor of philosophy at the University of California, Berkeley. He is the author of Philosophy of Mathematics and Mathematical Practice in the Seventeenth Century (Oxford University Press, 1996) and has edited or coedited several books, including The Philosophy of Mathematical Practice (Oxford University Press, 2008).
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.