New Dilemmas for the Prisoner
By Brian Hayes
A paradoxical game becomes even stranger with the discovery of novel strategies.
A paradoxical game becomes even stranger with the discovery of novel strategies.

DOI: 10.1511/2013.105.422
At the police station two suspects are questioned in separate rooms. Whoever talks first gets the better deal, the detective tells them. But they know that if they both keep quiet, they might beat the rap.
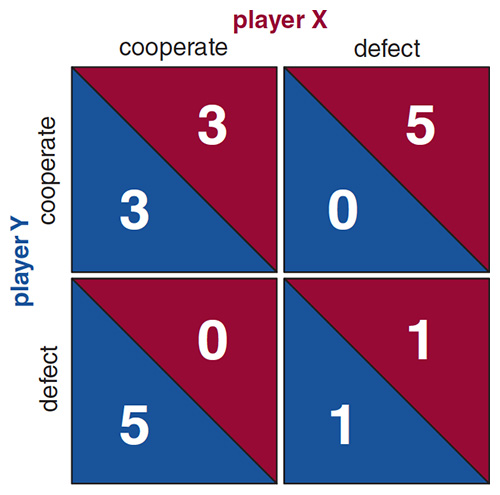
Television scriptwriters have drawn on this situation for countless plots. Game theorists have seized on it, too, but theirs is a more abstract and austere art form. They strip away the grimy crime-story details, leaving a formalized contest known as the Prisoner’s Dilemma. Gone is the threat of jail time; the game is played for points. Each player must choose either to cooperate (stay silent) or to defect (confess) and must make the choice before learning the other’s decision. If both players cooperate (cc), they earn three points each; if both defect (dd), they get just one point. If one player defects and the other cooperates (cd or dc), the defector receives five points and the hapless cooperator gets nothing.
Brian Hayes
A player devising a strategy for this game might reason as follows. “If my opponent cooperates, I’m better off defecting: I get five points rather than three. If my opponent defects, I still gain by defecting—one point versus none. Defection wins either way.” Of course the other player reaches the same conclusion. Thus they both wind up with a paltry single point, even though they know they could have gotten three points by mutual cooperation.
In a single game against a player you’ll never meet again, there’s no escape from this doleful logic. But the options are more complicated in Iterated Prisoner’s Dilemma (IPD), where you play a long series of games against the same opponent. The repeated encounters favor cooperative strategies that benefit both parties. A further refinement adds a Darwinian element to the game, with a population of players whose average scores determine their fitness and hence their probability of survival. In this case, too, cooperation can pay off.
Prisoner’s Dilemma has been a subject of inquiry for more than 60 years, not just by game theorists but also by psychologists, economists, political scientists, and evolutionary biologists. Yet the game has not given up all its secrets. A startling discovery last year revealed a whole new class of strategies, including some bizarre ones. For example, over a long series of games one player can unilaterally dictate the other player’s score (within a certain range). Or a crafty player can control the ratio of the two scores. But not all the new strategies are so manipulative; some are “generous” rules that elicit cooperation and thereby excel in an evolutionary context.
As a human predicament, Prisoner’s Dilemma is surely ancient, but as a formal game it was invented in 1950 by Merrill M. Flood and Melvin Dresher of the RAND Corporation. Interested in how human subjects deal with situations of conflict, they recruited two colleagues to play 100 matches in quick succession. Without any prearranged strategy, the players achieved mutual cooperation in 60 percent of the games.
Brian Hayes
A decade later Anatol Rapoport, a mathematician and psychologist at the University of Michigan, undertook further experiments and analysis. Then in the 1980s Robert Axelrod, also of Michigan, organized a series of IPD tournaments for computer programs. The big winner was one of the simplest strategies, called tit-for-tat, submitted by Rapoport. A tit-for-tat player always cooperates in the first round of a match and thereafter echoes the opponent’s previous move. Thus cooperation is rewarded with continued cooperation, and defection is punished by reciprocal defection.
Tit-for-tat is not an optimal strategy in the mathematical sense—guaranteed to prevail over all comers. As a matter of fact, it can never outscore an opponent; it always plays for a tie. Nevertheless, tit-for-tat performs remarkably well against a wide variety of other strategies. From the success of this simple rule Axelrod extracts some lessons for IPD players: Never be the first to defect; retaliate immediately when betrayed; relent after a single cycle of punishment.
Last year’s big surprise in Prisoner’s Dilemma research came from two distinguished polymaths. William H. Press of the University of Texas at Austin began his career as an astrophysicist, became expert in numerical methods of computation, and in recent years has turned his attention to problems in biology. Freeman J. Dyson of the Institute for Advanced Study in Princeton is renowned as a physicist, mathematician, author, visionary, and all-around deep thinker. The story of how Press and Dyson came to make their discovery is almost as interesting as the result itself, but I have room here only for the latter.
Press and Dyson studied IPD strategies in which the next move depends only on the immediately preceding round of play, ignoring all earlier history. It might seem that players with a longer memory would have an advantage against such forgetful opponents, but it turns out the “shortest-memory player sets the rules of the game.” Suppose your opponent has a “memory-one” strategy, but you base your moves on a deeper history—perhaps the past 10 or 100 plays. Press and Dyson show that there is a memory-one strategy that would have exactly the same effect on your opponent.
Every round of play in Prisoner’s Dilemma has four possible outcomes: cc, cd, dc, and dd. A memory-one strategy is a list of four numbers that specify a player’s probability of cooperating following each of these events. For example, the tit-for-tat strategy is encoded in the sequence of probabilities (1, 0, 1, 0): always cooperate after cc or dc, always defect after cd or dd. Another interesting strategy, nicknamed Pavlov, has the signature (1, 0, 0, 1): cooperate when you and your opponent have made the same choice (cc or dd), defect when you differed on the previous move (cd or dc). Both of these strategies are deterministic, with all probabilities either 0 or 1, but that’s not necessary. The strategy (½, ½, ½, ½) describes a player who chooses moves completely at random.
Given any two strategies, a computer program can simulate an IPD match between the players, keeping track of how often each outcome (cc, cd, etc.) appears in the results. With a long enough run, these frequencies converge to a “stationary state,” which represents the expected outcome of the match. A handy property of memory-one strategies is that it’s not actually necessary to run such a program; the stationary state can be calculated directly, without tracing through the game move by move. This shortcut makes it easy to explore a wide spectrum of game strategies.
Press and Dyson were doing just that when they noticed something odd: There are memory-one IPD strategies that allow you to seize complete control over your opponent’s score. Superficially, such a strategy looks like any other—it is encoded in a fixed set of four probabilities—but the strategy makes for a strangely one-sided game, where a player’s actions have no effect on his or her own score.
The one-sided rules are members of a newly recognized class of strategies that Press and Dyson call zero-determinant strategies. The name reflects the line of reasoning that led to the discovery—the strategies appear when the determinant of a certain matrix of probabilities is set to zero—but this fact is not especially helpful in understanding how the strategies work. What sets them apart from other memory-one strategies is the presence of certain algebraic relations between the four probabilities. For example, in one subset of zero-determinant strategies only the probabilities for cc and dd events are freely chosen; they then determine the cd and dc probabilities. As a result of such dependencies the stationary state of the game is controlled entirely by one player’s strategy, without any input from the opponent. This is a situation that “allows much mischief,” Press and Dyson write.
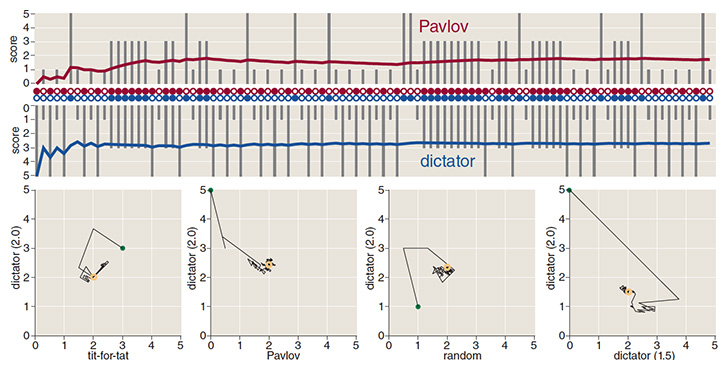
One mischievous strategy might be called the dictator: It unilaterally sets the other player’s long-term average score to any value between the mutual-defection payment and the mutual-cooperation payment. (For the standard payoff values 0, 1, 3, 5, that means anywhere between 1 and 3.)
Consider the strategy (4/5, 2/5, 2/5, 1/5), where the four numbers again indicate the probability of choosing to cooperate after cc, cd, dc, dd, respectively. If Y plays this strategy against X, then X’s average score per round will converge on the value 2.0 after a sufficiently long series of games, no matter what strategy X chooses to play. In the lower illustration on the previous page X responds to Y’s coercion with four different strategies, but in each case X’s average score gravitates ineluctably toward 2.0. It should be emphasized that dictating X’s score does not require Y to make any active adjustments or responses as the game proceeds. Y can set the four probabilities and then “go to lunch,” as Press and Dyson put it.
A second form of mischief manipulates the ratio between X’s score and Y’s score. If SX and SY are the players’ long-term average scores, the strategy allows Y to enforce the linear relation SY = 1 + M (SX – 1), where M is an arbitrary constant greater than 1. X has the option of playing an always-defect strategy, which consigns both players to the minimal payoff of one point per round. But if X takes any steps to improve this return, every increment to SX will increase SY by M times as much. Press and Dyson call the technique extortion. As an example they cite the strategy (11/13, 1/2, 7/26, 0), which sets M = 3. If Y adopts this rule, X can play always-defect (or tit-for-tat) to limit both players to one point per round. When X chooses other strategies, however, Y comes out ahead. If X plays Pavlov, the scores are approximately SX = 1.46 and SY = 2.36. To maximize his or her score, X must cooperate unconditionally, earning an average of 1.91 points, but then Y gets 3.73 points.
The discovery of dictatorial and extortionate strategies came as a great surprise, and yet there were precedents. Aspects of the discovery were anticipated in the 1990s by Maarten C. Boerlijst, Martin A. Nowak, and Karl Sigmund. Moreover, not all of the zero-determinant strategies are exotic ideas that no one ever thought of trying. Tit-for-tat, the most famous of all IPD rules, is in fact an extortionate zero-determinant strategy. It sets M = 1, forcing equality of scores.
Watching the coercive strategies in action (or playing against them), I can’t help feeling there is something uncanny going on. In a game whose structure is fully symmetrical, how can one contestant wield such power over the other? In the case of the dictatorial strategies, the symmetry isn’t so much broken as transformed: When I take control of your score, I lose control of my own; although there’s nothing you can do to alter your own score, you have the power to set mine.
The extortionate strategies can’t be explained away so easily. There really is an asymmetry, with one player grabbing an unfair share of the spoils, and the only defense is to retreat to the policy of universal defection that leaves everyone impoverished. IPD seems to be back in the same dreary jail cell where it all began.
One possible escape is to put the game in the larger context of evolutionary biology, where Prisoner’s Dilemma offers a framework for understanding how cooperation might arise in an environment that seems to reward only selfishness. The Darwinian mechanism “closes the loop” on the game: Each agent’s probability of success or failure depends on the composition of the entire pool of players, but the composition of that pool depends in turn on which players succeed and fail.
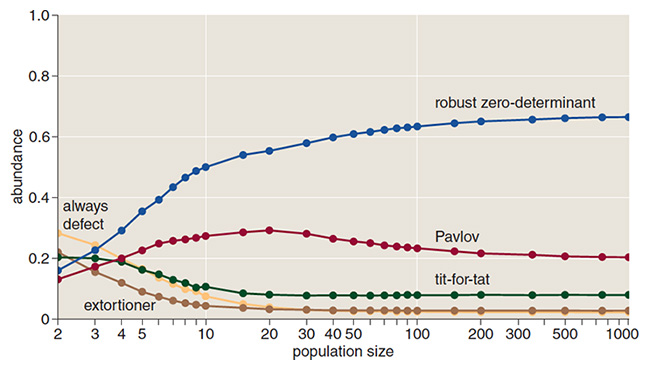
The simulations were run by and the data were supplied by Alexander J. Stewart and Joshua B. Plotkin of the University of Pennsylvania.
Soon after the Press-Dyson report appeared, Christoph Adami and Arend Hintze of Michigan State University tested various zero-determinant strategies in an evolutionary simulation. The coercive strategies did well against certain opponents, but eventually they were displaced by other players, most notably Pavlov. The reason is that a “nasty” player can become a victim of its own success. The reward for winning in an evolutionary game is to become more common in the population, with the result that you encounter more members of your own species. Dictators and extortionists do not thrive in that environment. Thus Adami and Hintze concluded that zero-determinant strategies are unlikely to evolve in the wild.
Over a long series of games one player can unilaterally dictate the other player's score.
But this is not the end of the story. It turns out that not all zero-determinant strategies are weapons wielded by brutes and bullies. Alexander J. Stewart and Joshua B. Plotkin of the University of Pennsylvania have identified a set of “generous” zero-determinant players that form a mirror image to the extortionate ones. An extorter tries to claim more than his or her fair share, but when this gambit fails must accept the low payoff for mutual defection. A generous player offers to accept less than a fair share of the average payoff as an inducement to mutual cooperation. In other words, the generous player is willing to be a patsy if that’s what it takes to secure cooperation.
Generous behavior might seem like a maladaptive invitation to abuse, but Stewart and Plotkin found otherwise. In a series of evolutionary experiments, the generous subset of zero-determinant strategies were the dominant species in all contests except those with a very small population (fewer than about 10 individuals). Stewart and Plotkin went on to prove that generosity is a “robust” strategy, able to establish itself and proliferate in a diverse population and then repel invasion attempts by others. Apparently it pays to put up with a little unfairness if that leads to greater opportunities for beneficial cooperation.
Is that the moral of the story? The players of these games are very simple and mechanistic; they are algorithms, not personalities. Nevertheless, it’s hard to resist giving them value-laden labels such as “extortionate” or “generous.” Axelrod’s analysis of tit-for-tat clearly echoes the fundamental principle of lex talionis: take an eye for an eye (but no more than that). The evolutionary results of Stewart and Plotkin hint at a new dispensation: Mercy is greater than justice.
©Brian Hayes
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.