
This Article From Issue
March-April 2001
Volume 89, Number 2
Page 110
DOI: 10.1511/2001.18.110
Counting is something we learn so early in life that we tend to dismiss it as a trivial skill, beneath the notice of mathematics. The recent U.S. presidential election suggests otherwise. Although most of the vote-counting controversies last fall concerned what to count rather than how to count, the counting process itself also proved to be imprecise and unreliable. Counting and recounting the same batch of ballots seldom gave the same total twice. Evidently, counting is not the utterly deterministic procedure we take it to be. There is some wiggle and wobble in it.
And ballots are not the only things we can lose count of. The Census Bureau has reported the U.S. population as 281,421,906, but no one believes this "actual enumeration" of the people is exact; the Bureau will deserve congratulations if even the first two of those nine digits are correct. Similarly, a U.S. Treasury web site displays "the public debt to the penny"; the last time I checked, the amount shown was $5,719,452,925,490.54, but again it's hard to believe that the accuracy of this figure matches its precision. Other purveyors of large numbers are more modest in their claims to exactitude. The New York Stock Exchange reports daily trading volume only to the nearest 100 shares. And the sign in front of my local McDonald's is stuck on "Over 99 billion served."
If counting is not a process we can count on, it seems prudent to look into the various ways it might go wrong. A theory of counting errors would describe the relation between the true number of things counted, which I'll designate N, and the number of counts actually registered, R. If you knew enough about the errors, you could predict R for any N. The inverse problem is harder: Given an observed count R, can you estimate the true N? The answer will not settle any election controversies, but it does lead into some curious byways of mathematics and computation.
Peano Arithmetic
The simplest kind of counting is based on tally marks. Start with a blank sheet of paper. For each object to be counted, make a mark on the page. When you're finished, the number of marks should match the number of objects.
This kind of counting is surely ancient, but it was given a formal, axiomatic basis just a century ago by the Italian mathematician Giuseppe Peano. Peano's scheme of arithmetic begins by postulating the existence of the number zero, or 0. The next number is defined as the successor of zero, written S(0). Next comes the successor of the successor of zero, or S(S(0)), then S(S(S(0))), and so on. Continuing in this long-winded way, you can count as high as you please; it's just a matter of applying the same rule over and over.
Brian Hayes
Peano's axioms belong to the ideal world of Platonic mathematics—the same world where geometric points are dimensionless, circles are perfectly round, and lines run straight and true to infinity. In that empyrean realm, chad are never hanging, and every count is full, fair and accurate. But that's not the world we live and count in.
When considering the causes of counting errors, it's helpful to have in mind a specific counting machine. A Peano counter might be a box with a long row of light bulbs on the front panel. Events to be counted enter the machine via a single input port; the input could be a wire, and the events pulses of voltage. The light bulbs are the machine's output. Initially, all the bulbs are dark. Each time an event is recorded, a bulb turns on—and thereafter stays on forever—so that the number of lit bulbs represents the number of events counted.
Such a machine could have many modes of failure. For example, a bulb could burn out, or a fuse could blow. Here I shall focus on one specific type of error: the possibility that a count fails to register. That is, a pulse arrives at the input, but no bulb lights up in response; the input is ignored, and the state of the machine remains unchanged. Such lost counts are assumed to be random and uncorrelated accidents, so that the machine operates probabilistically. If the counter is in state R when a pulse arrives, it moves to the correct successor state S(R) with probability p, and it stays in state R with probability 1–p.
Brian Hayes
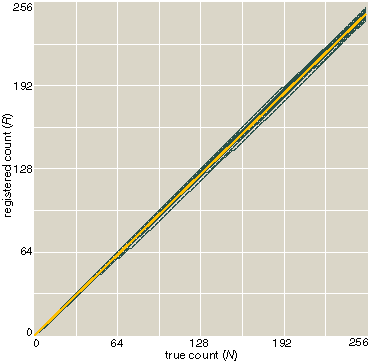
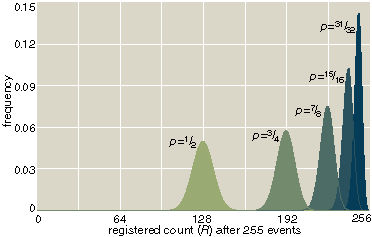
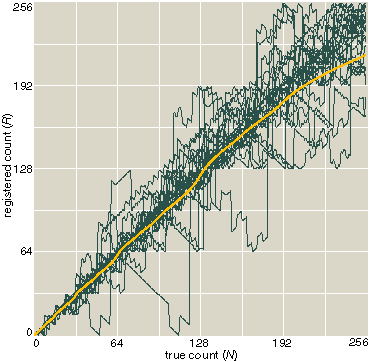
The basic mathematical properties of the probabilistic Peano counter are easy to describe. Because events can get lost but extra events are never introduced, the registered count R must always be less than or equal to the true count N. Also, the successive values of R must form a nondecreasing sequence: The counter can never run backwards. In any long series of counting trials, the mean value of R should be equal to pN. For example, with p = 0.75, a stream of 100 events will register 75 counts on the average. The extent to which individual results depart from the mean can also be measured statistically. The standard deviation of the distribution is proportional to the square root of p(1–p); thus the results are scattered most widely when p is 1/2, and the distribution gets narrower as p approaches either 0 or 1.
In a Peano counter with given values of N and p, you can easily gauge the probability of observing any value of R. However, predicting R when you know N is seldom what you want to do. More often, you are given R and you want to estimate N; that is, you know the tally announced by the county canvassing board, and you want to estimate how many votes were actually cast for each candidate. This inverse problem is subtler, especially when you don't know p. But if you can count the same set of objects many times, you can learn the shape of the distribution; then, the mean and the width yield an estimate of N.
Cascading Errors
Peano counting has the wholesome virtues of simplicity and transparency. Even in the presence of errors, it gives reasonably predictable results. There's just one problem: It never seems to accomplish anything. You start out with a heap of ballots, and after you count them you have a sheaf of papers covered with tally marks. Now you have to count the tally marks. If you do so by the Peano process, you wind up with another set of tally marks, which need to be counted in turn.
To make the count comprehensible, you have to introduce some higher-level structure. One familiar approach is to arrange the tally marks in groups, making four parallel strokes and then a fifth cross-stroke. In a second stage of counting, you can tally the groups of five, producing a page that has only one-fifth as many marks (plus a few leftovers, typically). Repeating the process, you count by twenty-fives, then by one-hundred-twenty-fives, etc. A slight variation on this procedure will have you counting in Roman numerals. But any such hierarchical scheme changes the error model. Suppose you make a mistake not in the original tally but in one of the higher-level consolidations; then the count changes not by one unit but by some power of 5.
Rather than analyze Roman enumeration in greater detail, let's proceed directly to counting in modern positional notation. Counting with tally marks is essentially a unary, or base-1, process. Adopting a base larger than 1 makes counting more efficient but also more treacherous.
Mechanical counters based on decimal notation are found in odometers and many other devices, including lever-actuated voting machines. In these mechanisms, input events drive a units wheel; each time this wheel completes a full turn, it jogs the tens wheel by a tenth of a revolution; then the tens wheel moves the hundreds wheel by the same amount, and so on.
Brian Hayes
Electronic counters are generally binary rather than decimal. A k-bit binary counter can count from 0 up to 2k–1; for example, an eight-bit counter runs up to 255 (which is 11111111 in binary). The basic building block for a binary counter is a device called a flip-flop, which has a single input, a single output and two internal states, labeled 0 and 1. In state 0, when the flip-flop receives an input pulse, it flips to state 1 but does nothing else. In state 1, when an input pulse arrives, the machine flops back to state 0 and also emits an output pulse. A k-bit binary counter requires k flip-flops. They are wired together in a cascade arrangement, with the output of each device becoming the input to the next. Initially, all the flip-flops are in the 0 state. The first input event flips the least-significant bit to 1. The next pulse flops this bit back to 0, and the output of the first flip-flop changes the next bit to 1. As successive pulses arrive, the cascade of flip-flops counts through the sequence of binary numbers: 0, 1, 10, 11, 100, 101, 110, etc.
What kinds of errors could upset this process? For one thing, the hazard that plagues the unary counter is still present: A signal might fail to register at the input port, so that the state of the counter would remain unchanged. But now there are other weak points as well. Each of the signals between stages of the flip-flop cascade is subject to the same kind of failure. And if a pulse between stages is lost in transmission, the consequences can be more drastic than a mere failure of the counter to advance.
Consider a four-bit counter in the state 0111 (equivalent to the decimal number 7). On the next input event, the rightmost flip-flop should change state from 1 to 0, issuing an output pulse that causes the next flip-flop to make a similar transition; when the signals have rippled all the way through the cascade, the next state of the counter is 1000 (decimal 8). But suppose the input pulse is recognized successfully, and so are all the intermediate signals except for the very last one, which is lost in transmission. Then all the 1 bits in the original state flop back to 0, but the 0 bit fails to flip to 1. As a result of this single error, the counter is reset to 0000, and the entire history of the count is wiped out.
Brian Hayes
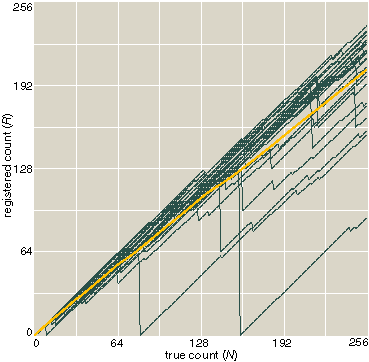
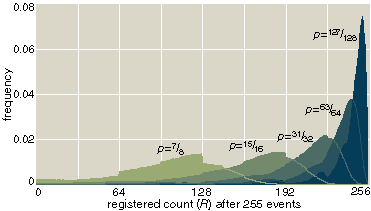
The statistics of such errors are clearly different from those of the Peano counter. It is still true that R is less than or equal to N, since there is no way for the recorded count to get ahead of the true count. But the sequence of R values is no longer guaranteed to be nondecreasing. Whenever the output of a flip-flop fails to propagate to the next stage, the count retreats; it is said to fall off a "Hamming cliff," named for the mathematician Richard W. Hamming. Moreover, the mean value of R is no longer equal to pN.
The trajectory of a cascade counter—the graph of R as a function of N—is typically a straight line ascending to the right with slope 1, interrupted at intervals by sudden falls from Hamming cliffs, after which the ascent resumes. Even with this erratic behavior, it seems possible that the mean value of R, averaged over many samples, would still be a simple function of N. But in fact the graph of the mean is neither a straight line nor a smooth curve; it has discontinuities near each power of 2. This nonlinearity makes estimating N from a knowledge of R even more challenging.
Mental Arithmetic
A week or two after the November election, while the perils and pitfalls of counting were still the topic of every conversation, I received two fascinating papers by Peter R. Killeen and Thomas J. Taylor of Arizona State University, giving an analysis of errors in cascade counters. The papers make no mention of ballot counting. Their motivation comes from a quite different area: the question of how people and animals judge duration. One hypothesis holds that a mental or neuronal counter accumulates pulses from a pacemaker oscillator. Killeen (a psychologist) and Taylor (a mathematician) investigate the effect that errors in the counter would have on the accuracy of biological timers. Along the way they discover a great deal about fallible counters in general.
Killeen and Taylor summarize the operation of a cascade counter by means of a transition matrix, which gives the probability of every possible transition between states. For example, here is the transition matrix for a four-state (or two-bit) binary counter that operates without error:
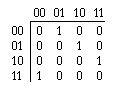
The first row indicates that if the current state of the counter is 00, the next state will be 01. The remaining rows show further transitions from 01 to 10, from 10 to 11, and finally (when the counter exceeds its capacity) from 11 back to 00. All other transitions have zero probability.
Now consider the corresponding matrix for a two-bit counter vulnerable to lost-pulse errors:
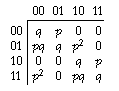
Here p is the probability of a correct counting transition, and q is equal to 1–p, the probability of a signaling failure. All the entries on the main diagonal are q, since this is the probability that the initial input will fail to register, so that the state of the counter remains unchanged. The entries on the "superdiagonal"—corresponding to a correct transition—are equal to p or powers of p. The transition from 00 to 01 has probability p, but the 01-to-10 transition has probability p2, because two bits must change and two signals must be transmitted. Along the "subdiagonal," some entries are the product of p and q, since the transition requires one success and one failure.
The beauty of the matrix representation is that it can trace the evolution of the counter's state through many transitions. A single application of the matrix gives the probability distribution after one input event. To find the probabilities after two inputs, simply multiply the matrix by itself. More generally, the state of the counter after N inputs is specified by the Nth power of the matrix.
From a study of the matrix power series, Killeen and Taylor measure the decay of information in a fallible cascade counter. In the low-order bits of the counter, the correlation between N and R diminishes continually, approaching a limit where the bits are essentially random. But correlations persist in the high-order bits, as long as the capacity of the counter is not exceeded. In a totally random process, the distribution of R would become flat, and all entries in the matrix would be equal to 1/N. But a fallible counter maintains a delicate balance between order and randomness. The distribution of R is neither flat (as in a random-number generator) nor smoothly peaked (as in a unary counter); it is a curve with curious lumps and oscillations and a hint of self-similarity, or fractal structure. The hint becomes patent when Killeen and Taylor examine the spectrum of the transition matrix—the series of characteristic numbers known as eigenvalues. The spectrum yields a classic fractal object called a Julia set. Viewed in this light, counting correctly is a rather dull pastime, and so is counting at random; but just the right dash of error turns it into a thing of beauty.
Shades of Gray
The main hazards to correct binary counting are those perilous Hamming cliffs. A tiny misstep—if it happens to come as a string of 1s rolls over to 0s—can put you over the edge. Engineers long ago confronted this problem in other contexts. For example, when encoding the angular position of a shaft as a binary number, the slightest misalignment can cause large uncertainty at a Hamming cliff. The standard remedy is an alternative to the ordinary binary numbers called a Gray code, which replaces the cliffs with gentler slopes.
Gray codes are named for Frank Gray, who was a physicist at Bell Telephone Laboratories in the 1950s and '60s, but the idea actually goes back to Emile Baudot, the French pioneer of the telegraph. The basic principle is to arrange the counting numbers in a sequence where each transition alters only one bit. For example, here is a three-bit Gray code: 000, 001, 011, 010, 110, 111, 101, 100. Note that all eight three-bit patterns appear in the sequence, and that each number differs from its neighbors at just one bit position. Many such codes exist, although the one shown here—called the reflected Gray code—is the most common.
Brian Hayes
Could Gray codes improve the accuracy of counting? At first, the idea seems promising: A missed event would set the count back by only one step, as in the unary Peano counter. But it's important to look at the internal details of a Gray-code counter. How does the counter generate the correct permutation of the binary numerals? For a shaft encoder, the sequence would be calculated in advance and permanently engraved in the hardware, but that's not a realistic option for a counter of larger capacity.
As it turns out, the obvious way to generate the reflected Gray code is to use an ordinary binary counter as an auxiliary. The position of the rightmost 1 bit in the auxiliary marks which bit should change next in the Gray code. But this implementation of the counter can hardly improve its error performance. At best, the Gray-code counter will inherit all the flaws of the binary counter. What's worse, when the binary and the Gray-code patterns get out of synch, the counter tends to go off on wild zigzag or crenelated trajectories. It can even start counting backwards. The behavior of the machine is fascinating, but it has little to do with the concept of counting.
I have looked for other ways to implement a reflected Gray-code counter, but the schemes I have tried turn out to be functionally equivalent to the auxiliary-counter method, and they suffer from the same error catastrophes. Of course it's entirely possible there's a clever method I've missed, or perhaps some Gray code other than the reflected one solves the problem.
Coding theory offers many other strategies for reducing error. The simplest device is a "parity bit," an extra bit that keeps track of whether the number of 1s in a binary number is odd or even. A parity check would combine particularly well with a Gray-code counter, because the number of 1s in a Gray code must alternate between odd and even. A 1990 report prepared for the Federal Election Commission recommends that ballot-counting machines be equipped with parity bits or other error-detecting devices.
How Not to Count
After the fall election, when I began thinking about the failure modes of counting machines, the subject seemed like a cute mathematical diversion of no practical application. I assumed that the error rate in real hardware would be so low that a machine would almost never fall off a Hamming cliff. After all, the computer on which I simulated fallible counters is itself built out of flip-flops and similar circuits; if these devices had any appreciable error rate, my program could not possibly run.
Nevertheless, it does appear that voting machines have occasionally stumbled over Hamming cliffs. The 1990 Federal Election Commission report tells the following story: "Consider, for example, the case of the election director who a few nights before the election realized while drifting off to sleep that although she had had her custodians check her lever machine counters to ensure that they changed over from 9 to 10, she had not had them check to ensure that they changed over from 99 to 100. In ordering such a check the next day, she discovered that one in twenty counters failed the test."
Whatever the source of error, counting is not something we can always rely on doing with absolute accuracy. Philip J. Davis writes: "As we get away from trivial sums, arithmetic operations are enveloped in a smog of uncertainty. The sum 12345 + 54321 is not 66666. It is not a number. It is a probability distribution of possible answers in which 66666 is the odds-on favorite."
Mathematically savvy election boards might acknowledge the irreducible fuzziness of counting, and treat it as a statistical process. In a close election the canvassing board could count the votes multiple times, and from the resulting distribution of Rs estimate N for each candidate. An alternative would be never to compile or publish vote totals with greater precision than the accuracy of the process can support. If we can only count with three significant figures, then the true outcome of an election cannot be 2,912,790 to 2,912,253. Both numbers would be more honestly expressed as 2.91 X 106. Of course this policy would increase the likelihood of ties, but that's just the point. If an election is too close to call, perhaps one should not call it.
Another option is to dispense with counting altogether. Fundamentally, in an election decided by simple majority rule, there is never a need to count ballots. It can all be done by the more primitive operations of sorting and matching. The procedure could be organized like a card game. Bring the candidates together in a room with all the ballots. Then let each candidate claim his or her ballot cards. (This is the hard part, of course, when decisions must be made about dimpled chad.) Then, once all the ballots are assigned, go around the room repeatedly, giving each candidate a turn to pitch a ballot into a discard heap. A candidate who runs out of ballots is eliminated. The last candidate with ballots in hand is the winner.
© Brian Hayes
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.