American Scientist

Researchers are constantly developing ways to decrease the size of transistors in order to increase the power and portability of computers, phones, and other electronic devices. As engineers approach the theoretical limits of size in traditional silicon transistors, some have turned their attention to quantum computing. Developments in this area can unlock powerful computing capabilities and expand our understanding of physics. Susan Coppersmith, the Robert E. Fassnacht and Vilas Professor of Physics at the University of Wisconsin, Madison, and a Sigma Xi Distinguished Lecturer, is at the forefront of these developments. She spoke about her research with American Scientist editor-in-chief Fenella Saunders. A video of the full discussion is available here.

A lot of people know the term quantum mechanics, but they don’t really understand the quantum part. Why is it called quantum mechanics?

A quantum is actually a jump. So if you have an atom, what happens is that you can say, “Well, what’s the light that comes out of an atom if you excite it?” This is how, for instance, fluorescent light works: You excite things and they let off light. In quantum mechanics, the light has a very well- defined color. That’s the wavelength of the light, but it turns out the color and the wavelength, the one tells you the other. If you drive it harder, it will go faster and your wavelength will go down. It turns out that, again, there were these things that were called the quantum jumps. And that’s how quantum mechanics got its name, because of the quantum jumps.

Quantum computing, though, is named more after the quantum mechanics than the quantum jumps. There I would say the key thing is that if you have a lot of different quantum mechanical objects and they can all talk to each other, it turns out that there are extra, what are nonlocal correlations, which are also called quantum correlations. Those can be used in information processing to be able to solve certain problems faster than in any classical system. That’s the origin of quantum computing, to use the quantum mechanics that you get when you’re thinking about atoms and individual electrons and little spins, to be able to do computations that would take you much longer in a regular computer, in a computer like your phone. Your phone is a pretty powerful computer, actually, but it only works with ones and zeros and it doesn’t work with quantum mechanical objects.

You mentioned spins. Electrons have a spin state, and part of their discretized or quantized nature is that they only have specific spin states. Is that right?

Right. Here, I’ll do my thumb. What happens is that if I think about my thumb and it’s just a spin going around, just like a top, I can imagine tilting my thumb and I can have it go at any angle. If I think about what component is vertical, I’d say, “It could all be vertical, or it could be quarter or half.” In quantum mechanics, it turns out that either it’s up or it’s down when you measure it. And then you can have different mixtures of up and down. So you can say, “So half the time it’s up and half the time it’s down.” Or “Three-quarters of the time it’s up and one-quarter of the time it’s down.” But always when you measure it, it’s either one or the other. That is really critical for when we’re making what are called the qubits in the quantum computer as opposed to the bits in the classic computer.

So measurement in quantum mechanics puts things in a state, or takes things out of a state?

Again, quantum mechanics is really strange, and we’re trying to take advantage of it. If I just take the spin and I can prepare it, it can be in a situation where it’s in what’s called a superposition of up and down. There’s good reason to believe that it’s in a superposition of up and down, and it’s not like, “It knows which one it’s in,” but you just don’t know. It’s not like you flip a coin and you don’t know whether it’s going to be heads or tails, but in principle you’d say, “Okay, if I could just really take a picture of the coin and look at it really carefully and figure out what it’s going to do, I would know.” In principle, you can’t know in quantum mechanics. That’s a really fundamental difference.

“Our intuition is all classical. To only get one result, that’s a classical statement,  so the measurement process is when you translate to us, to the classical world.”

• Facebook
• Twitter

But then when you measure it, of course, then you know. That means that something had to have changed. That’s something which is really important when you’re trying to make these things and get them to work: to realize the fundamental property is a measurement.

Once you’ve measured it, you’ve changed it, and then it’s set. Again, you could make it do something else, but if you just left it there, once you’ve measured it, you’ve changed it. But then after that, it’s in a new state and then goes on from there. It’s in a superposition, but then when you measure it, you destroy the superposition and then after that you don’t get it back unless you prepare it again. You’re just in the state after the measurement.

By the way, it sounds like a philosophical point, and it sort of is a philosophical point, but this is why Einstein really didn’t like quantum mechanics. He was an inventor of quantum mechanics, but then when the whole thing got codified, this property of measurement really bothered him. That was why he was not able to accept quantum mechanics as a correct theory of physics.

Is measuring something and putting it in a state, and having it be stable in that state, key for storing information?

That is true, you need a stable state, but actually, you want to keep the superposition. That’s one of the keys and why there’s a thing called quantum memory, because basically once you measure it, if you think of the spins as being either up or down, after you measure it, it has to pick one of those, but you want to encode this much more complicated information of the superposition of everything. And there’s a lot of it.

Then, when you want it to come out . . . [pauses]. We somehow only look at the classical world. Our intuition is all classical. If you do, you sort of figure, “I’ll get a result.” To only get one result, that’s a classical statement, so the measurement process is when you translate to us, to the classical world.

Transistors have been getting smaller and smaller so you can pack more of them into an available space. Is that what has allowed computers to become more powerful, the density of transistors in available space?

Yes, that’s one of the technological threads that’s pushing this. Basically the size of each transistor has gotten smaller and smaller over the past 50 years. Now we’re actually getting down to the point where the iPhone 7S technology is 14 nanometers. A nanometer is a billionth of a meter. But the thing is that the transistor is made out of silicon, and the separation between the atoms in the silicon is only about 1 nanometer. So you’re actually getting down to where the transistors themselves are only a few atoms. That has been why it’s believed that just making things smaller has to fail, because you can’t make a transistor that’s smaller than one atom, not out of silicon anyway. You have to do something else.

So quantum computing is a way of increasing the power of computation on a different axis. Instead of doing just the sheer shrinking axis, you’re changing the way the transistor works. It turned out that this was necessary to do anyway because again, as the transistors shrink, it’s easier for them to act quantum mechanically because as things get smaller and smaller, the quantum effects become more and more noticeable, and they affect the properties of the transistors a lot.

Everything went together in the sense of, “Let’s see if we can use the quantum mechanics to make the computer more powerful because we will not be able to shrink it.” If you just extrapolate, 2035 is the year when the size of the transistor would be one atom if the current trends were to continue. After that, we can’t do it anymore.

Why do the quantum effects become more noticeable as the transistors shrink down in size?

I think the way to think about it is that, okay, the way a regular transistor works is that, basically, it has a bunch of charges. It has a one or a zero and there’s a charge that has moved. But it’s not one electron that moves; it’s a bunch of electrons that move. If you didn’t know where one of them was, it’s okay because there might be a hundred of them, right? If one of them is misplaced, it’s still okay. But as you shrink things down, then what happens is just that the number of electrons you’re moving around goes down, and all of a sudden you’re faced with just one electron. Is it here or there? If you don’t know where it is, that’s a big mistake, so things become more uncertain just because the number of electrons that you’re working with is going down.

So then, in quantum mechanics, some aspects of it are just that the electrons are uncertain. You can think of them as fuzzy. We don’t know exactly where they are. Again, if you have a lot of fuzzy things, but they’re all sort of in more or less the right area, then you can be pretty certain what state you’re in, but as the number of electrons goes down, that fuzziness becomes more and more of a problem. That’s why, even if you just want to scale down classically, at some point you have to think about the uncertainties that come from the fact that it’s quantum mechanical.

People were kind of stuck thinking about this. People had talked at a very abstract level of, “Maybe we could use quantum mechanics to make more powerful computers.” So Richard Feynman wrote a very famous paper about this in the early 1980s. He was like, “We can make things smaller and then they’ll be quantum mechanical and there can be all this power from smallness.” But then in the mid-1990s, it became quite specific where there were certain problems, which were of great commercial interest—problems that Peter Shor showed you could solve more efficiently using the laws of quantum mechanics. That’s really what got people’s attention to the point of trying to say, “How do you make one of these things?”

That attention was totally unexpected at the time. Quantum computing went from being considered totally far out to “This would be really neat if we could build one of these things,” pretty quickly, for that reason. All of a sudden there were algorithms that would solve problems that would be very interesting if you could solve them.

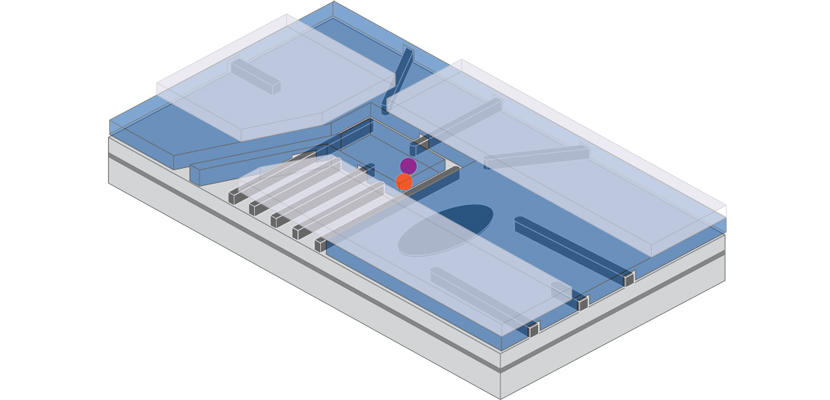
Your research is in quantum dots. How do they work, and how are they different from a standard transistor?

The thing about a quantum dot is that it’s very close to a standard transistor. There are different kinds of transistors, but the simplest one is where you have silicon and you have a piece of metal on top and there’s a thin oxide layer, so it’s called MOS, for Metal Oxide Semiconductor. You have a little oxide layer so you don’t get any current leaking through. Then you just put a big positive voltage and the electrons go to the surface. If you turn the voltage off, the electrons go away and then it’s off. So what you’re doing is, you’re just taking metal gates and you’re putting voltages on them, and they move electrons around. That’s basically how your computer, phone, TV, and car work at this point.

So what happens in a quantum dot is that you’re essentially doing the same thing, but you’re just doing it with fewer electrons. They’re called quantum dots because you have a region with an electron in it. Sometimes we have two electrons, but the number of electrons is really small. But the technology is as close as you could get to what we’re using now. That’s what makes it plausible that you could turn this into technology that’s scalable and also able to be integrated with classical electronics in a reasonably straightforward way.

It’s like we’ve been doing it all along in the sense of we’ve been taking gates and making the electrons by applying voltages to gates, but they’re quantum dots just because they don’t have very many electrons in them.

Do you have a sense of when quantum computing might hit a useful or commercial stage? Would it ever be a replacement for standard transistors?

It’s limited right now because the superconductors have to work at very low temperatures, so you’re not going to carry one around in your pocket.

You could imagine doing something portable with ion traps. They’ve been miniaturized greatly over the past decade. But they have a scalability issue because it turns out that one trap can only hold about 15 ions, so you have to couple different traps together. That coupling between different traps is very nontrivial. But if you had an application where 15 qubits would do it for you—in some efficient way, make it worthwhile—they could make an ion trap to do that tomorrow.

I think really the issue is error correction. Nobody has really demonstrated a scalable path to error correction. It’s surprisingly nontrivial. You’d say, “Look, I’ve got great gates and I can do whatever.” But it’s just harder than it sounds. I don’t know when that’s going to be solved, but having seen the progress between 2001, which is when I really started paying attention, to now, I’m pretty convinced it will be solved.

I think we’re looking at a 10- to 20-year time frame. But the error correction problem has to be solved before you can say, “Okay, now I know that we have commercial applications.” Because otherwise, what happens is that even if you have 99.9 percent, every time you make a new step, you have a little bit of error. So after you go a thousand steps, then you have no idea what you have. That means you can only do calculations of what is called bounded depth. That’s very limiting. For any size problem, you can only do a certain number of steps until you lose your accuracy. So error correction is really, really important. That’s challenging enough that I don’t think it’s going to be 10 years.

How does one build a qubit?

There are several different ways that people have proposed to make quantum computers. The progress has been really pretty amazing. People may have heard that IBM has a 5-qubit quantum computer online. Google has a quantum computer. They claim they’re going to have 20 qubits.

Each one is fascinating, and each one represents, of course, at this point a couple of decades of work that people have done. Again, one of the things that’s really neat about the field is that it’s almost like art, where you have a medium that you like to work in.

One kind of qubit uses superconductors. This is the most advanced at the moment, and it is the technology that Google and IBM are using. This method uses Josephson junctions, which use particular properties of superconnectivity to make a nonlinear element. A resistor is linear, in that if you put on a voltage, the current is linear in the resistance. To make any sort of interesting electronic device, you have to do something that’s nonlinear where the current is not proportional to the voltage. These Josephson junctions are nonlinear elements that they use. They’ve been able to engineer these things so that they’re just amazingly coherent, and their quantum coherence is just stupendous.